|
|||||||||||||||||||||||||||||||||||||||
![]()
|
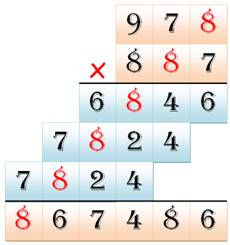
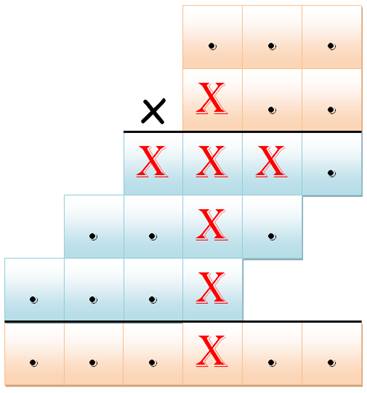
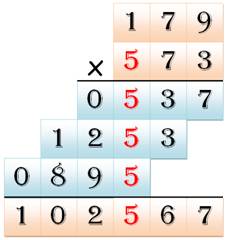
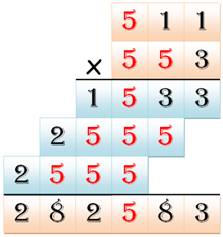
Puzzles arithmétiques Cette page fait suite à celle relative à la
multiplication à trous avec une diagonale en 123456. Il s'agit d'explorer d'autres
formes come la croix. On se limite à un seul chiffre répété dans le motif. |
|
|
||
|
Dans ce cas
avec 9, |
N,
M, P1, P2,
P2, R 111,
111, 111, 111, 111, 12321 911,
111, 911, 911, 911, 101121 911,
119, 8199, 911, 911, 108409 112,
222, 224, 224, 224, 24864 113,
333, 339, 339, 339, 37629 905,
555, 4525, 4525, 4525, 502275 915,
555, 4575, 4575, 4575, 507825 936,
665, 4680, 5616, 5616, 622440 936,
666, 5616, 5616, 5616, 623376 946,
666, 5676, 5676, 5676, 630036 946,
667, 6622, 5676, 5676, 630982 967,
777, 6769, 6769, 6769, 751359 967,
778, 7736, 6769, 6769, 752326 967,
779, 8703, 6769, 6769, 753293 228,
383, 684, 1824, 684, 87324 228,
388, 1824, 1824, 684, 88464 978,
885, 4890, 7824, 7824, 865530 978,
886, 5868, 7824, 7824, 866508 978, 887, 6846, 7824, 7824, 867486 978,
888, 7824, 7824, 7824, 868464 978,
889, 8802, 7824, 7824, 869442 989,
992, 1978, 8901, 8901, 981088 989,
993, 2967, 8901, 8901, 982077 989,
994, 3956, 8901, 8901, 983066 989,
995, 4945, 8901, 8901, 984055 989,
996, 5934, 8901, 8901, 985044 989,
997, 6923, 8901, 8901, 986033 989,
998, 7912, 8901, 8901, 987022 989,
999, 8901, 8901, 8901, 988011 999,
991, 999, 8991, 8991, 990009 999,
992, 1998, 8991, 8991, 991008 999,
993, 2997, 8991, 8991, 992007 999,
994, 3996, 8991, 8991, 993006 999,
995, 4995, 8991, 8991, 994005 999,
996, 5994, 8991, 8991, 995004 999,
997, 6993, 8991, 8991, 996003 999,
998, 7992, 8991, 8991, 997002 999,
999, 8991, 8991, 8991, 998001 |
|
|
|
|
|
|
|
|
|
||
|
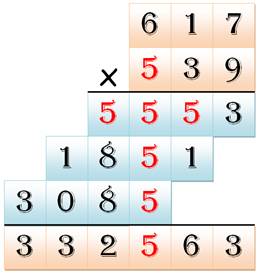
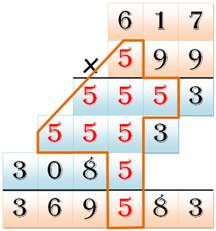
La résolution par raisonnement n'est pas évidente. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Voir Autres
multiplications en 5
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()