|
|||||||||||||||||||||||||||||
![]()
|
ÉNIGMES de TRANSVASEMENTS Mathématiques Nous
avons vu comment résoudre ce type d'énigmes. Essayons
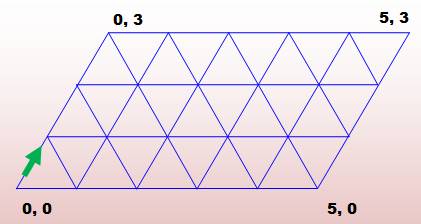
d'y apporter un brin de mathématiques. Nous reprendrons le diagramme triangulé. Les
premières observations vont être faites à partir de l'exemple célèbre (5,3 – 4): deux bidons de 5
litres et 3 litres avec lesquels obtenir 4 litres. Résumé Si la contenance des deux
récipients sont a et b (a > b), alors
La séquence des
transvasements peut être calculée en utilisant l'algorithme d'Euclide ou en
établissant la progression des nombres de raison b modulo a. |
|
|
||
|
Nous
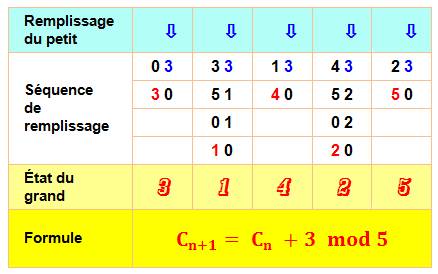
disposons de deux bidons de 5 litres et de 3 litres. Nous choisissons de remplir en premier le petit bidon. Le raisonnement
serait le même en commençant par remplir le grand bidon. Suivons le
diagramme du haut et formons le tableau du dessous.
Notez que
chaque opération de remplissage finit sa course sur le bas du diagramme. Les
valeurs obtenues dans le grand bidon sont en progression de 3 modulo 5. |
|
|
|
|
||
|
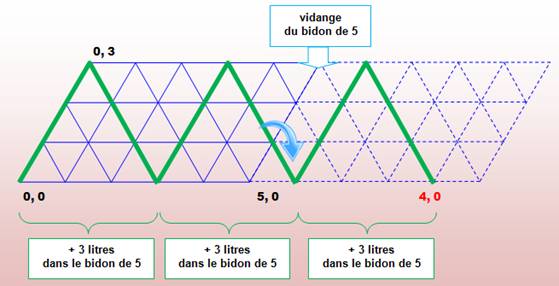
Avec pour
consigne d'obtenir 4 litres dans le grand bidon, nous pouvons suivre le
parcourt sur le diagramme. Mais
plutôt que de revenir en arrière (eau jetée), nous poursuivons sur un nouveau
diagramme accolé au premier |
|
|
|
Bilan |
Pour obtenir quatre
litres, il faut charger trois fois le petit bidon et jeter l'eau du gros une
fois.
|
|
|
Ou d'une
manière générale |
|
|
|
Analogie |
Cette méthode
consistant à prolonger le diagramme pour mieux oberver la solution, méthode
qui évite le repliement du diagramme sur lui-même, ressemble à celle utilisée
pour construire les carrés magiques: le tapis
magique. |
|
|
|
||
|
Comment
trouver les valeurs de a et b ? |
En procédant pas à
pas comme précédemment. Ce qui deviendrait délicat pour de grandes
valeurs. Heureusement il y a l'algorithme
d'Euclide. |
|
|
Voyons le
défi avec des récipients de 17 et 7 litres, sans l'algorithme. |
Progression de 7
mod 17: 7, 14, /4,
11, /1, 8, 15, /5, 12, /2, 9, 16, /6, 13, /3, 10, 0, 7, 14, 4 Toutes les valeurs
de 0 à 16 sont présentes (résidus). Le slash indique
l'action du modulo (une purge du gros bidon pour nous). Pour atteindre un volume de 1 litre, par exemple, il faut 5
remplissages du petit et 2 purges du grand.
Pour atteindre un volume de 3 litres,
il faut 17 remplissages du petit et 6 purges du grand.
En pratique: a =
quantité de nombres pour atteindre k; |
|
|
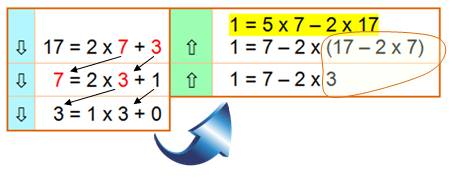
Algorithme
d'Euclide pour le cas avec 7 et 3 litres |
Decente à gauche:
quotient et reste deviennent dividende et diviseur pour l'étape suivante.
Remontée à droite:
valeur de 1 avec 7 et 3; puis avec 7
et 17. On retrouve bien la
relation: 5 x 7 – 2 x 17 = 1. |
|
|
Pour
avoir 1 litre |
Il faut emplir 7
fois le petit et purger 2 fois le grand. |
|
|
Conditions |
Les contenances des
deux récipients doivent être des nombres entiers premiers entre eux. Alors, il sera
posssible de trouver une solution à toute contenance entre 0 et la plus grand
moins un. Sinon la plus
petite valeur possible est le PGCD des
deux contenances. |
|
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
![]()