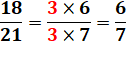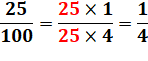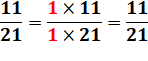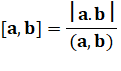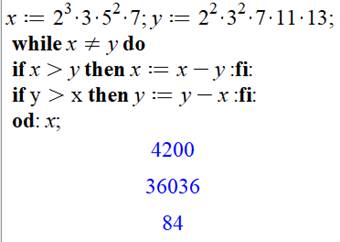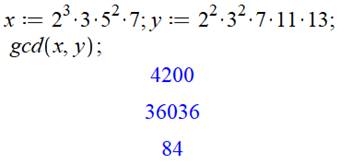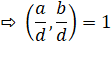théorie des nombres,facteurs,PGCD

NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 29/04/2020 Orientation générale DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Théorie des Nombres
Débutants Général	DIVISIBILITÉ				Glossaire Général
INDEX Divisibilité Calcul Théorie des nombres	Programme de 3^e	PGCD	Algorithme d'Euclide	Premiers entre eux
		PPCM	Sa programmation	Pgcd / Ppcm / Racine
		Sommaire de cette page >>> Approche >>> Notation et exemples >>> Programmation >>> Le triplet: retrouver le 3^e >>> Exploration >>> Propriétés >>> PGCD de plusieurs nombres >>> PGCD de 3 nombres >>> PGCD et PPCM >>> Exemples illustrés

PGCD

Plus Grand Commun Diviseur

Chaque nombre étant décomposable en facteurs premiers, on détermine le degré de cousinage des nombres en cherchant s'ils ont une tranche commune de facteurs premiers.

Le calcul du PGCD est utile pour simplifier les fractions.

Plus simplement dit

k est le PGCD de a et b veut simplement dire que

a et b sont des multiples de k.

Anglais: Greatest Common Divisor - GCD

Also: Highest Common Factor

Approche

Avec les nombres 4 et 6, cherchons la plus grande "longueur" commune.

Quelle est l'unité de mesure qui permet de mesurer exactement à la fois l'une et l'autre des barres?

Bien évidemment la réponse est: 2. Car, avec 2 comme unité de longueur, je peux mesurer à la fois 4, il faut 2 fois cette unité et 6, il faut 3 fois cette unité.

Exemples
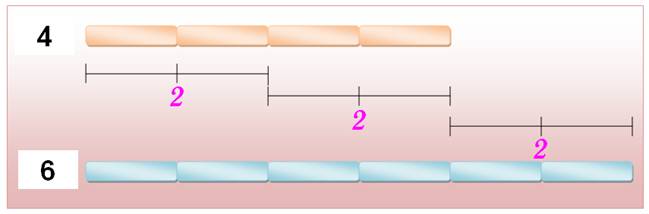
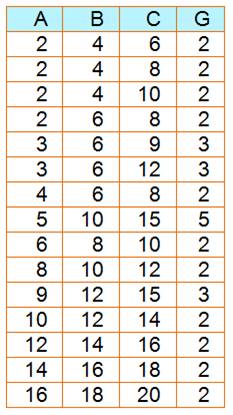
A = 18 B = 21 PGCD (A, B) A = 25 B = 100 PGCD (A, B) A = 11 B = 21 PGCD (A, B)	= 1 x 2 x 3 x 3 = 1 x 3 x 7 = 1 x 3 = 3 = 1 x 5 x 5 = 1 x 2 x 2 x 5 x 5 = 1 x 5 x 5 = 25 = 1 x 11 = 1 x 3 x 7 = 1 (A et B sont premiers entre eux)
Simplification des fractions Si est une fraction, numérateur et dénominateur peuvent être divisés par le PGCD pour obtenir une fraction irréductible. Voir Calcul avec l'algorithme d'Euclide

Remarque générale sur les notations
Normale	Abrégée	Signification
a.b	ab	Multiplication de a par b.
a.b	½ab½	Valeur absolue du produit a.b
PGCD (a,b)	(a,b)	Plus grand commun diviseur de a et b.
PGCD (a,b) = 1	(a,b) = 1	a et b sont premiers entre eux. a et b sont étrangers (autre nom).
PPCM (a,b)	[a,b]	Plus petit commun multiple de a et b.
PPCM (a,b) = a.b / PGCD (a,b)		Formule liant PGCD et PPCM.

Programmation

Programme complet

Instruction dédiée

Commentaires

Exemples de nombre en x et y.

Boucle (while … do) qui tourne tant que x est différent de y (qui s'arrête lorsque x = y).

Si x est le plus grand on lui retranche y; si y est le plus grand on lui retranche x.

Fin lorsque les soustractions successives donnent une valeur de x égale à celle de y. Y compris x= y = 1.

Fin de boucle (od) et impression de x.

Résultat: PGCD(4 200, 36 036) = 84

Notez que tout logiciel mathématique comporte une instruction donnant directement le PGCD. Avec Maple, il s'agit de gcd (greatest common divisor).

Voir Programmation – Index

Le triplet – PGCD à trou

Sachant que 54 est le PGCD de (378 et A), quelles peuvent être les valeurs de A ?

378 et A sont tous deux des multiples de 54:

378 = 2 x 3 x 3 x 3 x 7

54 = 2 x 3 x 3 x 3

Et A vaut toute valeur multiple de 54

soit A = 54 k

À l'exception banale de k = 7, pour laquelle les deux nombres seraient 378 et leur PGCD serait évidemment et banalement 378.

Exploration

PGCD (A, B)

Premiers entre eux

10 est 4 fois premiers

avec les nombres qui lui sont inférieurs.

12 est 4 fois premiers

avec les nombres qui lui sont inférieurs.

1 000

On observe la symétrie par rapport à A = 1 000

pour les nombres premiers avec 1000.

990

991

992

993

994

995

996

997

998

999

1000

1001

1002

1003

1004

1005

1006

1007

1008

1009

1010

1000

Voir Table des PGCD

Propriétés
Notation normale			Notation abrégée
PGCD (a, 1)	= 1		(a, 1)	= 1
PGCD (a, a)	= a		(a, a)	= a
PGCD (a, b)	= PGCD (b, a)		(a, b)	= (b, a)
PGCD (a , b)	= PGCD (a + b, b)		(a , b)	= (a+b , b)
PGCD (a , b) ou	= PGCD (a – b, b) = PGCD (a, b – a)		(a , b)	= (a-b, b) si a>b = (a, b-a) si a<b
PGCD (a, b)	= PGCD (a + kb, b) = PGCD (a – kb, b)		(a, b)	= (a + kb, b) = (a – kb, b) >>>
PGCD(a, b, c)	= PGCD (PGCD(a, b), c) = PGCD (a, PGCD(b, c))		(a, b, c)	= ((a, b), c) = (a, (b, c))
PGCD (am, an)	= a.PGCD (m, n)		(am, an)	= g.(m, n)
Si PGCD (b, c) = 1, PGCD (a, bc)	= PGCD(a, b). PGCD(a, c)		Si (b, c) = 1, (a, bc)	= (a, b) (a, c) >>>
d = PGCD(a,b)	PGCD (a/d, b/d) = 1		d = (a,b)
D = ax + by	PGCD (a, b) D		D = ax + by	(a, b) D
PGCD (a . c, b . c)	= PGCD (a, b) x c		(a.c , b.c)	= (a , b) . c
PGCD (a / d, b / d)	= PGCD (a, b) / d		(a/d , b/d)	= (a , b) / d
PPCM (a, PGCD (a, b))		= a	[a, (a, b)]	= a
g = PGCD (a, b) <=> a / g et b / g sont premiers entre eux. Pour qu'un diviseur commun à a et b soit leur PGCD, il faut et il suffit que les quotients par ce diviseur soient premiers entre eux.

Voir Propriétés des nombres premiers entre eux (PGCD = 1)

PGCD d'une somme

On donne (a, 4 ) = 2 et (b, 4) = 2, montrez que (a + b, 4) = 4.

Si (a, 4 ) = 2, cela veut dire que a et 4 sont divisibles par 2, mais que a n'est pas divisible par 4. On peut former la division euclidienne: a = 4k + 2. De même: b = 4k' + 2.

Et leur somme: a + b = 4(k + k') + 4 qui est divisible par 4.

En écriture PGCD: (a + b, 4) = 4.

Simplification du calcul d'un PGCD

Calculez (998, 996).

Utilisation de la propriété: (a, b) = (a – kb, b).

(998, 996) = (998 - 996, 996) = (2, 996) = 2.

Autre exemple:

(204, 153) = (204 – 153, 153) = (51, 153) = (51, 3x51) = 51

Exemple algébrique:

(3n + 4, n + 1) = (3n + 4 – 3(n + 1), n + 1) = (1, n + 1) = 1

PGCD avec un nombre certainement composé

Si (b,c) = 1,

(a, bc) = (a, b) (a, c)

Nécessité que b et c soient premiers entre eux pour que cette formule soit vraie, même si elle peut être vraie dans d'autres cas.

Formule complète

Si ((a,b), (a,c)) = 1, alors (a, bc) = (a, b)(a, c)

Si PGCD ( PGCD(a,b), PGCD(a,c) ) = 1,

alors PGCD (a, bc) = PGCD (a, b) x PGCD (a, c)

PGCD de plusieurs nombres

Propriété

PGCD (a, b, c) = PGCD (PGCD (a, b), c)

Pour trouver le PGCD de plusieurs nombres, on peut remplacer deux nombres par leur PGCD.

Exemple

PGCD (240, 252, 792) = PGCD (PGCD (240, 252), 792)

= PGCD (12), 792)

= 12

PGCD (322, 546, 611) = PGCD (PGCD (322, 546), 611)

= PGCD (14), 611)

= 1

Si le PGCD est égal à 1, les nombres sont tous premiers entre eux dans leur ensemble.
Attention! Ils peuvent ne pas être premiers deux à deux
Exemple: 6, 10 et 15.

PGCD de 3 NOMBRES

Quelques exemples & Premières valeurs pour G croissant

PGCD et PPCM
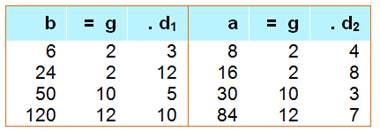
Si a ne divise pas b mais s'ils ont en commun un nombre g qui les divise tous les deux, alors a et b sont tous deux composés.	Dans ce cas, il existe un nombre g tel que: b = g . d₁ a = g . d₂ a, b, d₁ , d₂ et g sont des nombres entiers. Exemple
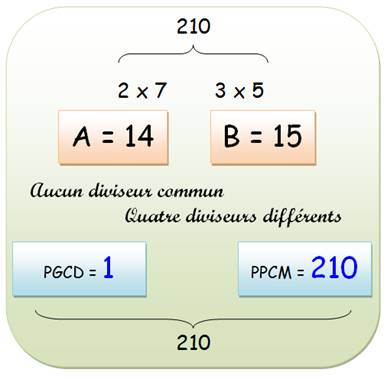
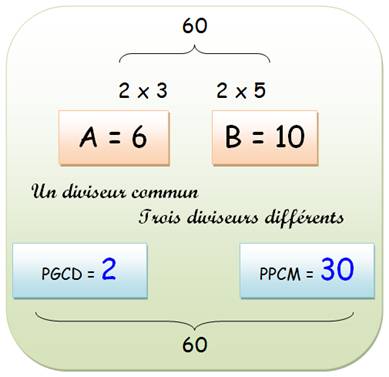
Pour caractériser le degré de divisibilité, on a inventé deux nombres spéciaux: PGCD : plus grand commun diviseur. PPCM: plus petit commun multiple.	Exemple 14 et 15 sont premiers entre eux. 14 = 2 x 7 15 = 3 x 5 PGCD = 1 PPCM = 210

Deux exemples de calcul

Suite	PPCM PGCD en théorie des nombres PGCD er recherche de nombres premiers
Autour	La division en pratique c'est quoi? – Débutant La division en résumé c'est quoi? – Glossaire Divisibilité par un nombre donné Diviseurs: calculs et facteurs premiers PGCD d'une suite de nombres consécutifs
Voir	Des jeux sur les partages Diviseurs: nombres parfaits Fraction continue Jeux et puzzles – Index L'arithmétique de l'horloger Le calcul mental Nombres Premiers Pseudo Premiers Pseudo Premiers Absolus Théorie des nombres – Index
Cette page	http://villemin.gerard.free.fr/ThNbDemo/PGCD.htm