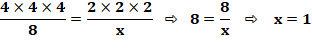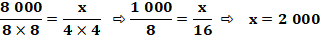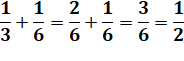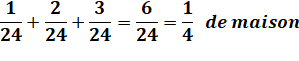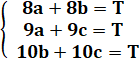|
||||||||||||||||||||||||||||||||||||||||
![]()
|
Travaux à quelle vitesse? Chaque ouvrier travaille à
son rythme. En les regroupant à quelle vitesse s'exécute le travail? Ou
l'inverse: on connait le travail en groupe, retrouver la vitesse de travail
de chacun. Calculs en double proportion. |
|
Il
faut 5 minutes à 5 elfes pour emballer 5 cadeaux. Combien
de temps pour 50 elfes et 50 cadeaux à emballer ? Cinq
pêcheurs pêchent cinq poissons en cinq heures. Combien
de pêcheurs pour prendre vingt poissons en une heure? |
|
|
||
|
Problème
|
Solution 1 En huit jours, il creuse: 4x4x4 = 64 m3 Or, le nouveau trou a un volume de: 2x2x2 = 8 m3 Un seul jour de plus sera nécessaire pour creuser le second trou. Solution 2 Rapport des volumes:
|
|
|
|
||
|
Problème
|
Solution 1 8 hommes en 8 jours => 8 000 carreaux 4 hommes en 8 jours => 4 000 4 hommes en 4 jours => 2 000 Solution 2 Rapport entre les activités:
|
|
|
|
||
|
Problème
|
Solution
Voir Fractions
au même dénominateur |
|
|
Problème
|
Solution
|
|
|
|
||
|
Problème
|
Résolution On note a, b et c la
quantité de pièces produites en un jour par chacun. Les données permettent
d'écrire un système de trois équations
dont la solution est indiquée dand le tableau. La
colonne de droite donne le numéro de l'équation. Celle de gauche indique les
opérations sur les équations selon leur numéro.
Solution L'ouvrier A produit 7 pièces
par jour, soit 3 jours pour les 24; L'ouvrier B est à 5 pièces
par jour, soit 4,8 jours; et L'ouvrier C, avec une pièce
par jours, mettra 24 jours. |
|
|
|
|||
|
Cette énigme est semblable à la précédente.
Elle est rapportée avec ces nombres par Ozanam. |
|||
|
Problème
|
Mise en équation
|
||
|
Résolution La colonne de droite donne
le numéro de l'équation Celle de gauche indique les
opérations sur les équations selon leur numéro.
Solution a, b et c sont les vitesses
d'exécution journalière du travail Durée de travail pour tout le champ par chacun des ouvriers:
|
|||
|
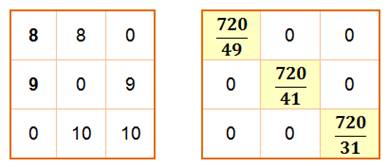
Notons les coefficients des
trois équations du départ dans un tableau et également les résultats: Ces tableaux s'appellent des
matrices et celui de
droite est le résultat de la diagonalisation de la première. |
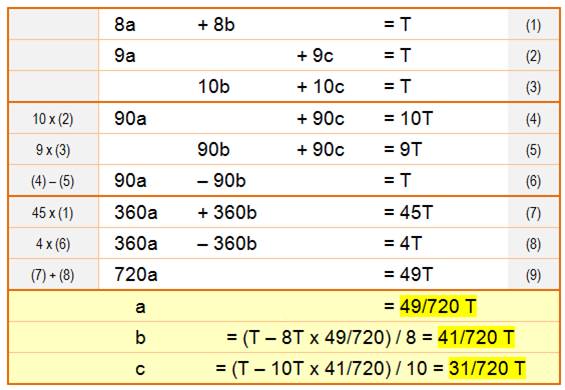
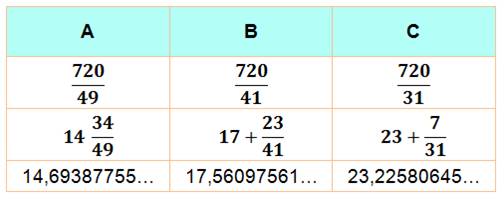
À gauche, les paramètres sont liés (8a + 8b pour faire T) alors qu'une
fois diagonalisée, les paramètres sont
purs (720/49 a pour faire T). |
||
|
Énigme Il
faut 5 minutes à 5 elfes pour emballer 5 cadeaux. Combien
de temps pour 50 elfes et 50 cadeaux à emballer ? Réponse express
|
|||||||||
|
Énigme Cinq
pêcheurs pêchent cinq poissons en cinq heures. Combien
de pêcheurs pour prendre vingt poissons en une heure? Attention Même si ce n'est pas dit dans l'énoncé,
il s'agit de moyennes.
En effet, avec beaucoup de chance, il se pourrait qu'un seul pêcheur ramène
les vingt poissons en seulement quelques minutes. L'énigme serait sans
intérêt. Réponse express
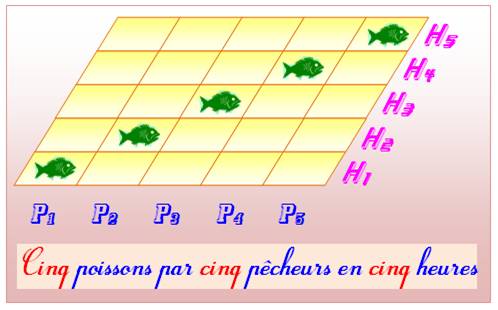
Solution avec illustration montrant comment s'y prendre Quel
que soit le moment de la pêche de chacun, on peut imaginer sans changer le
résultat final que le premier pêcheur (P1) à pêché un poisson la
première heure (H1), le deuxième, la deuxième heure, etc. On aurait pu dire que le premier pêcheur a
pêché les cinq poissons dans la première minute, puis rien pendant 4 h 59 min et aucun poisson pour les autres. Le
résultat serait le même. L'illustration
représente notre hypothèse et montre qu'en moyenne, il faut 5 heures à un
pêcheur pour prendre un poisson.
Pour
avoir vingt poissons en une heure, il faut reproduire vingt fois la première
ligne, soit 20 x 5 = 100 pêcheurs. Il se trouve alors que vingt d'entre eux
ont la chance de prendre un poisson durant cette heure, alors que les
quatre-vingts autres restent bredouilles. Mais, ils sont nécessaires dans le
calcul de la moyenne. Dit-autrement: on ne sait pas a priori lesquels vont
être chanceux. Note: si j'avais placé les cinq poissons sur
la ligne du bas (soit la première heure), je n'aurais pas respecté les données de l'énoncé. |
Retour / Énigme des
poules pondeuses
![]()
|
Suite |
|
|
Voir |
|
|
Cette
page |
![]()