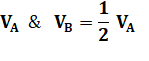énigme de l'escalier roulant, vitesse double

NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 19/01/2019 Orientation générale DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique
	ÉNIGMES
Débutants Vitesse	Durée				Glossaire Vitesse
INDEX Jeux	Escalier	Tonneau	Robinets	Nénuphar
	Escalier (double)	Travaux	Vitesse
		Sommaire de cette page >>> Anne et Bernard sur l'escalator >>> Solution avec calcul de ratio (pente) >>> Solution avec calcul de vitesse >>> Solution graphique

ESCALIER ROULANT

Escalier mécanique / Escalator

Vitesse double l'un de l'autre

escalator logo.jpg Deux personnes gravissent l'escalier en mouvement, l'un progresse à une vitesse double de celle de l'autre. Les données semblent manquer. Comment résoudre cette énigme ? Plusieurs méthodes.

Anne et Bernard sur l'escalator

Pendant qu'Anne monte une marche, Bernard (frimant) en monte deux.

Arrivés, Bernard a compté 30 marches alors qu'Anne en a compté 20.

Quelle est la quantité de marches de l'escalier au repos.

L'énigme ne semble pas facile à résoudre. Manque-t-il des données ?

Non ! Mais le raisonnement n'est pas simple. Par quel bout le prendre ?

NB. On cherche la quantité de marches défilant pour monter une personne immobile du bas en haut de l'escalier en mouvement (et non la totalité des marches de l'escalator avec ses marches cachées).

Note: Les deux prénoms sont souvent "Alice et Bob" (pour deux prénoms en A et B).

Solution avec calcul de ratio (pente)
On suppose que: les deux personnes partent en même temps sur l'escalier; la personne la plus rapide est arrivée en haut de l'escalier. On raisonne alors sur la position de l'autre.
Bernard est en haut en:	30 marches
Au même moment, Anne qui va deux fois moins vite, n'a fait que:	15 marches
Pour arriver en haut, il lui reste	15 marches à faire avec l'escalier.
Or on sait que, pour arriver en haut, il faut qu'elle en fasse encore par elle-même:	20 – 15 = 5 marches
Bilan: il lui reste à monter:	15 marches dont 5 par elle-même
On effectue le ratio sur tout son parcours complet de 20 marches.	60 marches dont 20 par elle-même
Soit le total des marches:	60 marches pour l'escalier
Notez que Bernard monte 30 marches pour 30 avec l'escalier; pour Anne, c'est 20 marches seule et 40 avec l'escalier	En marches par seconde: Vitesse Bernard = Vitesse escalier; Vitesse Anne = 1/2 Vitesse escalier.

Voir Illustration graphique de cette solution avec une énigme semblable

Solution avec calcul de vitesse
Calcul avec les vitesses totales: celles avec la personne en mouvement sur l'escalier. N'ayant aucune indication de durée, on fixe une unité de temps arbitraire.
Appelons T le temps d'avancement d'une marche de l'escalier (le temps qu'une marche s'efface en haut de l'escalier).		T secondes pour une marche
Si l'escalier compte n marches, le temps de montée de l'escalier en restant immobile sur une marche est :		n.T secondes pour l'escalier complet
Bernard va plus vite que cela. Il monte 30 marches, autant de marches que l'escalier n'aura pas à faire avec lui pour arriver en haut. L'escalier lui-même monte donc:			(n – 30) marches
Le temps de montée de l'escalator avec Bernard dessus:			(n – 30) T
Ce qui prend pour chacune des 30 marches que Bernard monte:			(n – 30) T / 30
Bien ! Mais, on sait qu'Anne va deux fois moins vite:			(n – 30) T / 15
Comme pour Bernard, on peut évaluer la vitesse d'Anne. Elle monte 20 marches que l'escalator n'aura pas à faire pour l'emmener en haut. Soit sa vitesse:			(n – 20) T / 20
Deux expressions pour la vitesse d'Anne:	(n – 30) T / 15 = (n – 20) T / 20
Résolution	20n – 600 = 15n – 300 5n = 300 n = 60 marches

Solution graphique
Une solution lourde, mais qui peut rassurer quant au raisonnement. Il est vrai que les problèmes sur les vitesses réservent parfois des pièges.
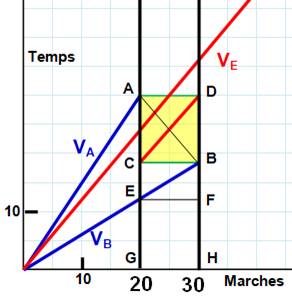
Le graphique montre le temps en fonction de la quantité de marches. La diagonale rouge représente le mouvement propre de l'escalier. Les traits bleus épais indiquent le mouvement propre d'Anne et de Bernard. Attention axes inversés (le temps est en ordonnées). La vitesse est exprimée en secondes par marche. Avec ce mode, la vitesse de Bernard est moitié de celle d'Anne (moins de secondes pour le même nombre de marches).
Il s'agit de déterminer la vitesse propre d'Anne et celle de Bernard.
Autrement dit: trouver A et E tels que:		GA = 2 GE avec AB = CD et CD étant parallèle à V_E
Coordonnées des points:
Le point B est aussi connu à partir du point A par la diagonale AB.
Le point E est aussi connu à partir du point B par la diagonale BE.
Rapprochement des égalités pour E:	Pour les ordonnées
Résolution La vitesse du fils est double de celle de l'ascenseur et celle du père est exactement celle de l'ascenseur.		En secondes par marche
Bilan pour les marches:		Bernard 30 marches = > Escalier 30 marches Total 30 marches.
Vérification avec Anne:		20 marches à la vitesse V_E + 2 V_E Rapport: 3 => 20 x 3 = 60 marches