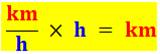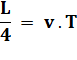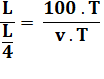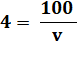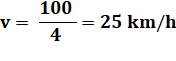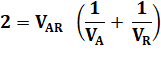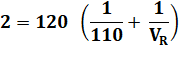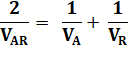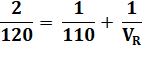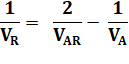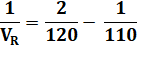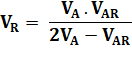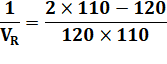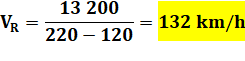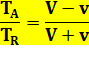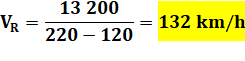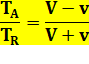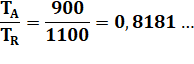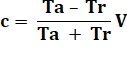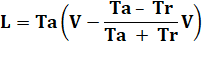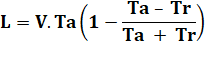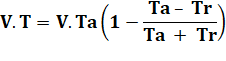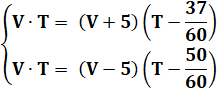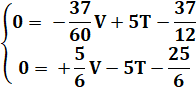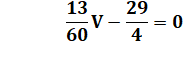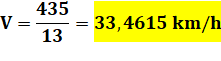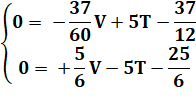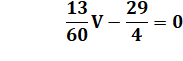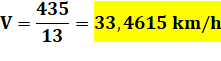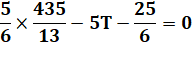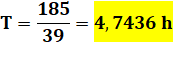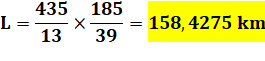|
||||||||||||||||||||||||||||||||||||||||
![]()
|
Vous
rouliez à combien, Monsieur? –
J'étais tout seul, Monsieur
le Juge! |
|
|
|
Voir Pensées & humour
|
Problèmes de VITESSE Énigmes
classiques basées sur le calcul de
vitesse. Rappels
|
N'hésitez pas
à voir la rubrique vitesse, spécial
débutant!
Niveau
primaire
|
|
||
|
Contexte
Essayez vous-même et vous aurez du mal à croire à
un score si médiocre de nos enfants! |
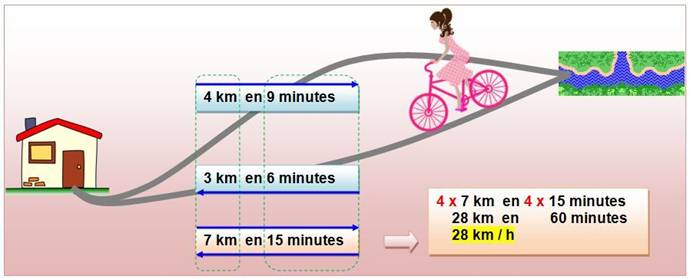
Problème posé Hélène vient de recevoir un nouveau vélo, avec un compteur de vitesse
fixé sur le guidon. Le compteur de vitesse indique à Hélène la distance qu’elle parcourt
et sa vitesse moyenne pour le trajet. Hélène a roulé de chez elle jusqu’à la rivière qui se trouve à 4 km.
Il lui a fallu 9 minutes. Elle est rentrée chez elle en prenant un raccourci
qui fait 3 km. Il ne lui a fallu que 6 minutes. Quelle était la vitesse moyenne d’Hélène (en km/h) lors de cette
balade, aller et retour à la rivière? |
|
SOLUTION
/ Voir Enseignement
![]()
NIVEAU COLLÈGE SIMPLE
|
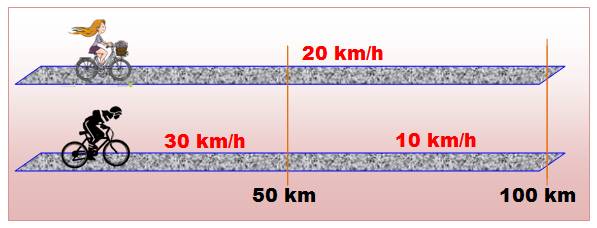
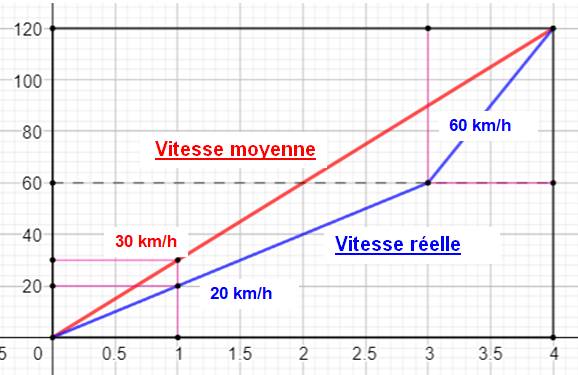
La
fille roule régulièrement, alors que le garçon frime en roulant à toute
allure puis, se voit contraint de finir à petite vitesse. C'est la fille qui
arrive la première. |
Fille
Garçon
|
Voir Bicyclette
de Dudeney / Sens
de marche du vélo selon sa trace
|
Ce
coureur fait 60 km à 20 km/h. Il
lui reste encore 60 km. À
quelle vitesse doit-il pédaler pour atteindre une vitesse moyenne de 40 km/h
? Saurez-vous
être plus doué que ChatGPT ? |
|
|
||||||||||||||||||||||||||||||||||
|
Énigme Un cycliste fait
10 km à la vitesse de 15 km/h. Il faut dire qu’il avait un vent contraire et
espère aller plus vite au retour. Peut-il dépasser
son record de vitesse moyenne sur l’aller-retour qui est de 30 km/h.
Longueur (km) = vitesse (km/h) x temps (heure) Notes Longueur ou distance Temps ou durée |
Réponse Il a déjà utilisé
tout le temps qui serait nécessaire (en
jaune dans le tableau) pour établir une vitesse moyenne de 30 km/h. Il
lui faudrait alors une vitesse infinie pour parvenir à égaler son record.
C'est donc impossible. Calcul Trajet aller: 10 km à 15 km/h lui prend 0,66 h (40 minutes). Son record: 20 km à 30 km/h c'est aussi 40 minutes. Trajet retour: il lui reste 0 minutes pour égaler son
record.
Et s’il avait roulé à 20 km/h à l’aller
Il lui faudrait faire le retour en 0,166 … h = 10
minutes. |
|||||||||||||||||||||||||||||||||
|
|
||
|
Énigme Une piste
cycliste. Jean termine les 20 tours alors qu'il en reste encore 2 à Pierre.
Chacun à maintenu sa vitesse constante. Quel est le
rapport entre la vitesse de Jean et celle de Pierre? |
Réponse Le rapport est
20/18 = 10/9 Calcul 20
= VJ .T 18
= VP .T Le temps étant le
même. En divisant ces
deux équations:
|
|
|
|
||
|
Problème D’un
côté, il y a vous qui êtes capable de ramer à 7 km/h sans courant. Mais
dans cette rivière, vous remontez un courant dont la vitesse est de 3 km/h. De
l’autre, à 14 km en amont, un pécheur perd son bouchon qui se met à descendre
le courant. Dans
combien de temps croiserez-vous le bouchon ? |
Astuce : Le
bouchon descend le courant pendant que vous, vous êtes contraint par le même courant.
Sans ramer, vous descendriez à la même vitesse que le bouchon. Les deux
phénomènes se compensent et le courant n’a pas d’influence sur la durée. Solution Vous
devez parcourir les 14 km à la vitesse de 7 km/h, soit 2 heures d’effort. |
|
Niveau
collège avancé
|
|
||
|
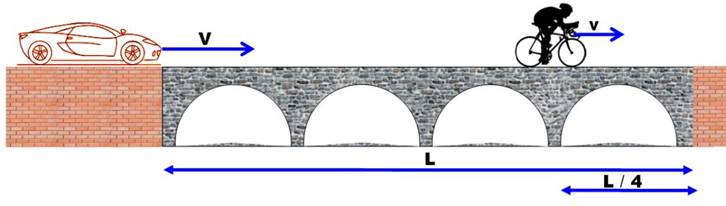
Problème
Commentaire Ce problème semble impossible à résoudre à
première vue tant il doit manquer des données! Ce n'est pas possible? Néanmoins, s'il doit y avoir une solution, on se
dit que: s'il reste encore un quart de trajet pour le cycliste, alors, il
doit bien y avoir un rapport 4 qui va intervenir. Nous avons la
conviction que si le cycliste dégage
le viaduc à une vitesse quatre fois moindre que l'automobile, cela va être
suffisant. Vérifions par le calcul. Illustration
Résolution |
||
|
Voiture et vélo doivent
arriver au bout du viaduc en même temps, soit dans: |
T heures |
|
|
Durée du parcours par la
voiture: |
|
|
|
Durée du parcours par le
vélo: |
|
|
|
En divisant ces égalités: |
|
|
|
En simplifiant |
|
|
|
Et la vitesse du cycliste
devient: |
|
|
|
|
|||
|
Un
problème dont la réponse est surprenante lorsqu'on omet de remonter à la
formule de base. |
|||
|
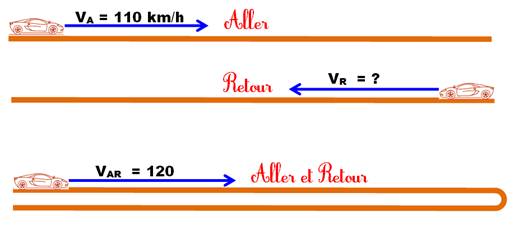
Problème Un automobiliste
a noté sa vitesse sur le trajet aller: 110 km/h Il sait
également qu'il a roulé à une moyenne de 120 km/h sur le trajet aller-retour. Il
affirme à sa femme qu'il a respecté la limitation de vitesse sur autoroute.
Est-ce vrai? |
|
||
|
Commentaire Ici, un
raisonnement intuitif n'est pas très possible. Le calcul va montrer que la
réponse n'est pas 130 km/h comme on pourrait le penser. Réponse |
|||
|
1) Trajet
aller |
|
|
|
|
2) Trajet
retour |
|
|
|
|
3) Trajet
aller et retour |
|
|
|
|
Dans
cette troisième équation remplaçons TA et TB par leurs valeurs
calculées avec les équations 1 et 2 |
|
|
|
|
En
divisant tout par L |
|
|
|
|
En
divisant tout par VAR = 120 |
|
|
|
|
Calcul de
VR |
|
|
|
|
Et sa
valeur numérique |
|
|
|
|
La réponse
n'est pas 130, le nombre symétrique de 110 par rapport à moyenne de 120. Mais
un peu plus: 132 km/h. Il a
dépassé la vitesse autorisée, Oui, mais de peu! |
|||
|
Graphe donnant la vitesse de retour selon la
vitesse de l'aller pour une moyenne de 120 km/h
|
|||
Voir Moyenne harmonique
|
|
||
|
Situation et question Un avion
fait un trajet aller et retour sans vent. Mais, ce
jour-là, il subit un vent constant qui le pousse à l'aller et le freine au retour.
Quel est le temps mis par l'avion pour faire l'aller et le retour? Réponse rapide Le même
temps que sans vent, car la poussée compense le freinage! Non, ce n'est pas la bonne réponse. Anglais An aeroplane flies against
the wind from A to B in 8 hours. The same aeroplane returns from B to A, in
the same direction as the wind, in 7 hours. Find the ratio of the speed of
the aeroplane (in still air) to the speed of the wind. |
Sans vent 2L = 2VT Avec vent de vitesse v L = (V + v) TA L = (V – v) TR 2L = (V + v) TA+ (V – v) TR Les durées aller et retour sont
effectivement différentes dans le rapport:
Exemple V = 1000 km/h et v = 100 km/h
Sur un trajet de 10 000 km TA =10 000 / 1100 = 9,09 h TB =10 000 / 900 = 11,11 h Et TA / TB
= 9,09 / 11,11 = 0,8181… Total TV = 20,20 h Au lieu de (sans vent) 2T =20 000 / 1000 = 20 h
|
|
|
|
||
|
Nous
sommes sur une rivière en canoë et faisons l'aller et le retour entre A et B.
Soit sept
heures pour l'aller-retour. Sans
courant, quelle serait la durée de l'aller-retour? Nous ramons toujours de la même manière avec ou
sans courant. |
On peut imaginer que les forces qui ont ralenti à
la montée vont s'équilibrer avec les forces qui poussent à la descente. Voyons le calcul et découvrons une surprise comme les problèmes de vitesse savent nous
en réserver. Notations V notre vitesse propre en ramant toujours de la
même manière, c la vitesse du courant, L la longueur du trajet, et T le temps mis sans courant. |
|
|
La longueur est
identique dans tous les cas |
L = 4 (V – c) = 3 (V +
c) = V T |
|
|
Avec les deux
premières relations |
4V – 4c = 3V + 3c |
|
|
En reprenant la
longueur |
L = 4V – 4c = 4V – 4 x
V/7 = 24 V/7 |
|
|
Puis avec la
troisième expression de la longueur |
L = V T = 24 V/7 T = 24/7 = 3,43 heures |
|
|
Temps aller et
retour sans courant |
2T = 6,86 heures Et non pas 7 heures comme nous l'avions envisagé. |
|
Calcul
formel et interprétation**
|
La longueur est
identique dans tous les cas |
L = Ta (V – c) = Tr (V
+ c) = V T |
|
Avec les deux
premières relations |
Ta.V – Ta.c =
Tr.V + Tr.c |
|
En reprenant la
longueur |
|
|
Puis avec la troisième
expression de la longueur |
|
|
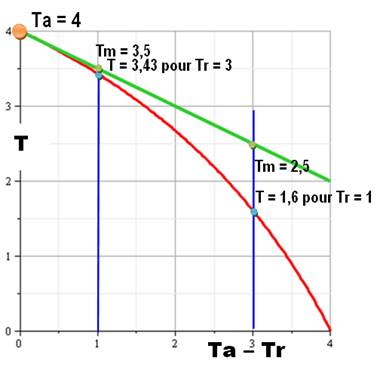
Pour Ta = 4 heures, graphe de T en fonction de Ta - Tr Si le temps de retour avec le courant est raccourci
de 1 heure (Tr = 3), alors le temps moyen avec le courant est (4 + 3 ) / 2 =
3,5 et le temps sans courant est T = 3,43. Une différence de 3,5 – 3,43
= 0,07 h = 4,2 min. Si le courant est vraiment très fort et que
l'écart passe à 3 heures (Tr = 1), le temps moyen est de (4 + 1) / 2 = 2,5 et
le temps sans courant T = 1,6. Une
différence importante de 2,5 – 1,6 = 0,9 = 54 min Plus le courant est fort et plus l'écart se
creuse. À la limite avec un retour instantané (Tr = 0 et Ta – Tr = 4), le
trajet sans courant est lui-aussi instantané (T = 0). |
|
|
|
|||
|
Problème En
augmentant la vitesse de 5 km/h, on gagne 37min. En
diminuant la vitesse de 5 km/h on perd 50 min. Calculer
la vitesse et la durée du parcours. |
On rappelle la formule magique: L = V.T Longueur
parcourue = Vitesse multipliée par le Temps |
||
|
Solution Nous
avons ici trois situations que nous exprimons avec notre formule, sachant que
le trajet est le même dans tous les cas (L = constate). Notez la
division des minutes par 60 pour exprimer le temps en heure. |
|
||
|
En
réduisant à deux équations à deux inconnues. |
|
||
|
En
développant: |
|
||
|
En
simplifiant avec VT: |
|
||
|
En
ajoutant, en remarquant que cette opération a pour effet d'éliminer V. |
|
||
|
Soit la
valeur de V: |
|
||
|
Valeur de
T: |
|
||
|
Valeur de
L: |
|
||
Merci à Robert T pour ce problème
![]()
|
|
||
|
Problème posé Hélène vient de recevoir un nouveau vélo,
avec un compteur de vitesse fixé sur le guidon. Le compteur de vitesse indique à Hélène la
distance qu’elle parcourt et sa vitesse moyenne pour le trajet. Cette première partie donne un
contexte, mais elle est totalement inutile à l'énoncé. La suite ne comporte
évidemment aucun piège. Je surligne en jaune les données importantes. Hélène a roulé de chez elle jusqu’à la rivière qui se trouve à 4 km. Il lui a fallu 9 minutes. Elle est
rentrée chez elle en prenant un raccourci qui fait 3 km. Il ne lui a fallu que 6 minutes. Quelle était la vitesse moyenne d’Hélène (en km/h) lors de cette balade, aller et retour à la
rivière? |
||
|
Rappel des données |
Aller: 4 km en 9 minutes Retour: 3 km en 6 minutes |
|
|
Conclusion |
Trajet A/R: 7 km en 15 minutes (un
quart d'heure) |
|
|
Pour faire une heure |
15 minutes, c'est un quart d'heure. Il faut quatre fois un quart d'heure pour faire
une heure. |
|
|
Quelle distance en une heure? |
Nous avons: 7 km en 1/4 d'heure. En quatre quarts d'heure (= une heure): 4 x 7 =
28 km. |
|
|
Vitesse moyenne |
28 km / heure |
|
|
Illustration
Rappel La vitesse
est une distance (km) divisée par une
durée (heures) qui donne par conséquent
des km / h. La vitesse
moyenne est la vitesse sur la totalité du parcourt: distance totale (7
km) divisée par la durée totale (0,25 h). Soit 7 |
||
Source: Éducation – Ce
n’est peut-être pas un problème de mathématiques – Mathieu Lang – 3 mars
2016
![]()
|
Voir |
|
|
Aussi |
|
|
Cette page |
|
Question Ce
coureur fait 60 km à 20 km/h. Il lui reste encore 60 km. À
quelle vitesse doit-il pédaler pour atteindre une vitesse moyenne de 30 km/h
? Saurez-vous
être plus doué que ChatGPT et déjouer le piège? Réponse ChatGPT La
vitesse à réaliser est 40 km (sans doute
en faisant (20 + 40) / 2 = 30 km/h). Un
calcul de vitesse moyenne
au lieu d'une moyenne harmonique. Réponse attendue À
30 km/h de moyenne pour parcourir les 120
km, il lui faut: 120/30 = 4 heures. En
réalité, il a déjà parcouru les 60 premiers kilomètres en: 60/20 = 3 heures Il
ne lui reste plus qu'une heure (4 – 3) pour parcourir la seconde partie de
60km. Il
lui faudra réaliser une vitesse de 60 / 1 = 60 km/h. En formules mathématiques
En graphique
|