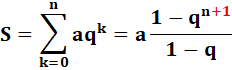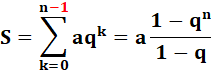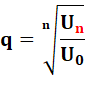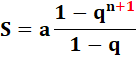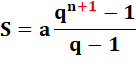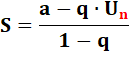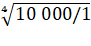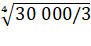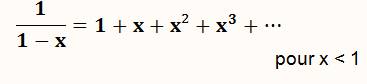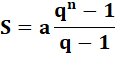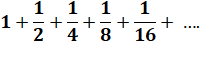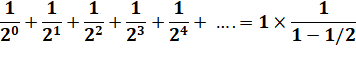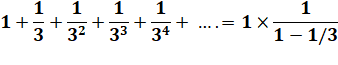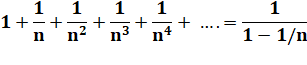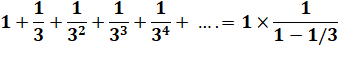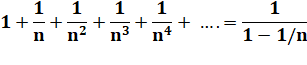|
|||||||||||||||||||||||||||||||||||||||||
![]()
|
SUITE
GÉOMÉTRIQUE ou PROGRESSION
GÉOMÉTRIQUE Nombres
successifs tels que ch appelé
raison. On s'intéresse
particulièrement à la somme qui est nommée: Série géométrique. |
Anglais: Geometric
progression, common ratio (= raison)
Voir Moyenne géométrique / Suite
et Série
|
Somme d'une série géométrique de raison q et de premier
élément a. Attention aux bornes: n ou n – 1. |
|
|
|
|
Approche |
|
|
|
|
|
|
||||||||||||||||||||||
|
Défi Pour
me récompenser donne-moi:
Quelle
est la somme que je recevrai ? Calcul
Astuce
|
||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Somme des puissances de 2
S n = 2
n+1 – 1 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Somme des puissances de 5
Mise en formule
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Généralisation
à somme des puissances de A
Exemple avec A = 10 1 + 10 + 100 + 1000 +
10 000 = S4 = (105 – 1) / (10 – 1) = 99 999 / 9 = 11
111 |
Voir Somme des
entiers et des puissances / Table
des sommes de puissances
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Généralisation Avec
une progression géométrique, le terme suivant est obtenu en multipliant le
terme précédent par un même facteur appelé raison q. Un = a . qn Et
la somme est de la forme: Sn = a.q0 + a.q1 + a.q2
+ … + a.qn Autrement
dit, une progression
en puissance Rappel des notations
Formules générales
Exemple 1, 10, 100, 1000, 10
000 U4 = 10 000 (le cinquième terme, car la numérotation
commence à zéro). q = S = (1 – 105)
/ (1 – 10) = 11 111 3, 30, 300, 3000, 30
000 U4 = 30 000 q = S = 3 (1 – 105)
/ (1 – 10) = 33 333 Suite en Exemples de calcul |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Sn = a + aq
+ aq² + … + aqn qSn = aq + aq² + … + aqn + aqn+1 Sn – qSn = a
– aqn+1 Sn = a(1 – qn+1)
/ (1 – q) |
|
|
||
|
|
q = 2 Sn =
a (2n+1 – 1) |
|
|
|
– 1 < q < 1 Slim = a / (1 – q) |
|
|
|
||
|
|
q = 1/2 Slim
= a / (½) = 2a |
|
|
|
Slim3 = a / (2/3) = 1,5a Slim4 = a / (4/3) = 1,33 …a Slim5 = a / (5/4) = 1,25a etc. |
|
|
|
||
|
|
La
nouvelle séquence de nombres est une PG. |
|
|
|
La
nouvelle séquence de nombres est une PG. |
|
|
|
La
nouvelle séquence de nombres est une PA >>> |
|
|
Alors,
m est la moyenne géométrique de a et b. |
m
= a.r et b = m.r En
divisant:
|
|
|
|
||
|
|
|
|
|
|
|
|
|
Calcul de 0,
999 ... = 0, 9 + 0, 09 + 0, 009 +
... = S |
0 = 0,9 q = 1/10 S = 0,9 / (9/10) S = 1 |
|
|
|
= 2
Suite >>> |
|
|
|
= 3/2 |
|
|
|
= n (n – 1) |
|
Voir exemple en Calcul de l'aire du flocon de neige
/ Inverses des puissances
Démonstration géométrique quasi-muette
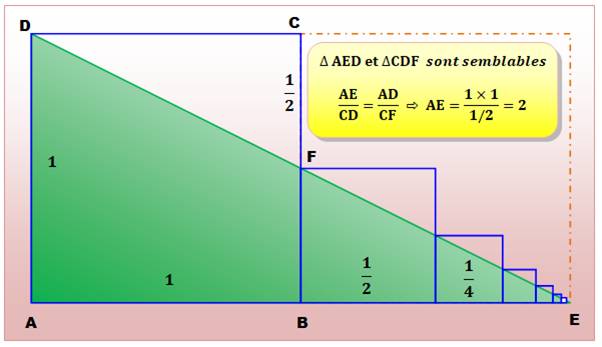
English corner

Source: Infinite
geometry series
![]()
|
Retour |
|
|
Suite |
|
|
|
|
|
DicoNombre |
|
|
Cette page |