|
Édition du: 06/03/2024 |
|
INDEX |
GRAPHES |
||
Faites
un double-clic pour un retour en haut de
page
![]()
|
Énigme des CINQ MAISONS
Problèmes de raccordements
problématiques entre maisons ou entre villes. On connait le cas classique du raccordement
de trois
maisons à l'eau, au gaz et à l'électricité. |
||
|
|
Sommaire de cette page >>> Raccordement de cinq villes >>> Énigme des cinq maisons et
leurs chemins >>> Les cinq maisons totalement raccordées |
Débutants Glossaire |
Anglais: water,
|
Le problème des cinq villes Autrefois,
cinq petites villes ont décidé de construire des routes reliant chaque paire
de villes. Même
si les villes disposaient de suffisamment d'argent pour construire des routes
comme elles le souhaitaient, il était très important que les routes ne se
croisent pas (car les panneaux STOP n'avaient pas encore été inventés). De
plus, les tunnels et les ponts n'étaient pas autorisés. Est-il
possible pour toute ville de construire une route vers chacune des quatre
autres villes sans créer d'intersections ? |
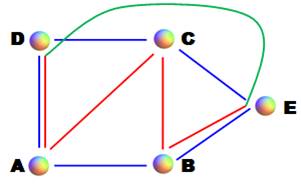
Solution Ce
type de raccordement entre cinq villes est impossible. S'il
existait une solution, alors pour chaque ordre
possible du parcours des cinq villes, il existerait un circuit qui les
visite toutes les cinq dans l'ordre et revient à la première, sans retour en arrière.
Prenons
le circuit bleu: A, B, E, C, D Vous
constaterez que le circuit rouge ne peut pas être entièrement à l'intérieur
du circuit bleu, ni entièrement à l'extérieur du circuit bleu. Par
conséquent, il existe au moins une ville pour laquelle le circuit rouge passe
de l'intérieur à l'extérieur du circuit bleu. Donc,
pas de raccordement complet possible sans intersection ! |
|
|
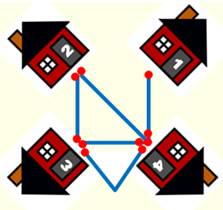
Énigme Chaque
maison est réunie à certaines autres par autant de chemins que l'indique son
numéro. La
figure montre une solution pour quatre maisons. Trouver
la solution pour cinq maisons. Énigme proposée par M.
Launay Piste Chaque
chemin comporte évidemment deux extrémités (points rouges). Pour
quatre maisons, on compte les points rouges au seuil de chaque maison. Il en existe:
1 + 2 + 3 + 4 = 10, soit effectivement assez pour réaliser 5 chemins (10 /
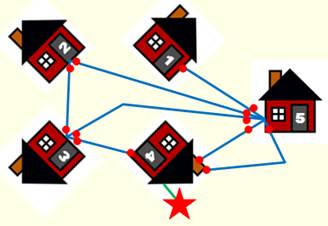
2). Pour cinq maisons La
quantité de bouts de chemins (points rouges devant chaque maison) sera 1 + 2
+ 3 + 4 + 5 = 15. Ce
nombre est impair,
et il ne permet pas de réaliser un nombre rond de chemins. Il n'y pas de solutions (étoile rouge). |
Quatre maisons – Exemple de solution
Cinq maisons – Impossible
|
|
|
Généralisation La
quantité T de points rouges pour n maisons est la somme des entiers de 1 à n.
Ce sont les nombres
triangulaires: T = ½ n (n + 1) Une
solution n'existe que pour les nombres triangulaires pairs. |
Liste des cas possibles: [n, T] [3, 6], [4, 10],
[7, 28], [8, 36], [11, 66], [12, 78], [15, 120], [16, 136], [19, 190], [20,
210], … Finalement,
ce sont les nombres n divisibles par 4, accompagnés des nombres précédents,
comme 4 et 3. |
|
|
Énigme Ce
sont cinq maisons raccordées par un réseau routier à voie unique. Il y a
exactement une route entre chaque paire de maisons. Le
réseau est tel qu'il est toujours possible d'aller d'une ville à une autre,
dans un sens ou dans l'autre, en empruntant ces routes, en passant
éventuellement par d'autres villes. Quelle
est la quantité de routes ? |
Piste Il
s'agit de compter toutes les configurations possibles et d'en retirer les cas
non recevables. Le
calcul n'est pas simple. Diverses
solutions figurent dans le document
2017 AIME cité en référence Solution La
solution est la quantité de tournois fortement
connexes de cinq sommets, soit 544. |
|
![]()
|
Voir |
|
|
Aussi |
|
|
|
|
|
Cette page |
![]()