NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 24/09/2023 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	JEUX
Débutants Général	ÉNIGMES				Glossaire Général
INDEX JEUX	Classiques	Famille	Graphes	Villa
	Chapeaux	Truel	Chasseur	Pastis
		Sommaire de cette page >>> Problème n°1: Numéros des habitations >>> Problème n°2 : Prix des plaques >>> Numéros et leurs prix >>> Autour de 100 >>> Énigme de la maison du maire

ÉNIGMES avec les NUMÉROS des VILLAS

Numéros qui se suivent ou non.

Prix des plaques pour apposer les numéros sur la villa.

Comment s'y prendre ?

Énigme de la maison du maire.

Pb1: Numéros des habitations
Problème Il y a 75 maisons dans la rue. Numérotation classique avec les numéros impairs qui se suivent et de même pour les pairs pour l'autre côté de la rue. Sachant que le dernier numéro pair est 62, quel est le numéro de la dernière maison du côté impair?	Solution Du côté pair, du n°2 au n°10, il y a 5 maisons (10/2). Jusqu'au bout de la rue jusqu'au n°62, il y a 62/2 = 31 maisons. Il reste 75 – 31 = 44 maisons de l'autre côté. Du côté impair, du n°1 au numéro 11, il a 6 maisons selon le compte: (11 + 1) / 2. Jusqu'au bout de la rue, il a 44 maisons. Le dernier n° est tel que n + 1 = 2 x 44 = 88. La dernière maison du côté impair porte le numéro 87.

Pb2: PRIX des plaques numérotant les villas

Les plaques pour composer les numéros des villas sont intitulées du nom de la ville* et elles coûtent: la valeur du chiffre indiqué sur la plaque, sauf le 0 qui vaut 10. J'ai acheté toutes les plaques pour moi et mes deux voisins: J'ai demandé 8 € de plus à mon voisin avant moi, et J'ai demandé 9 € de moins à mon voisin après moi. Quels sont les numéros des villas? Nous avons moins de 200 villas dans la rue.

* Pas de possibilité d'échanger le 9 contre un 6.

Vous pouvez résoudre l'énigme sans cette contrainte.

Les malins achèteront des plaques n°6 pour le 6 et pour le 9, faisant ainsi des économies.

Merci à Jean-François Capdet pour ces remarques pertinentes

NUMÉROS ET LEURS PRIX
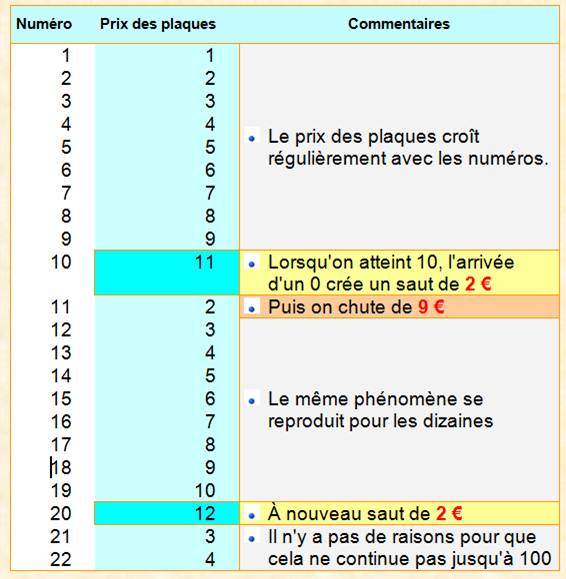
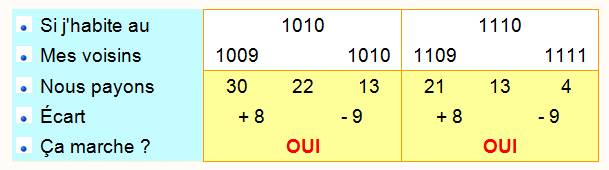
Voyons les premiers numéros Illustration Pour ces valeurs, on constate que
Le voisin d'avant paie 1 € de moins, ou 9 € de plus mais jamais 8 € de plus comme l'exige notre problème.	Le voisin d'après paie 1 € de plus, 2 € de plus, ou 9 € de moins ça marcherait de ce côté

AUTOUR de 100

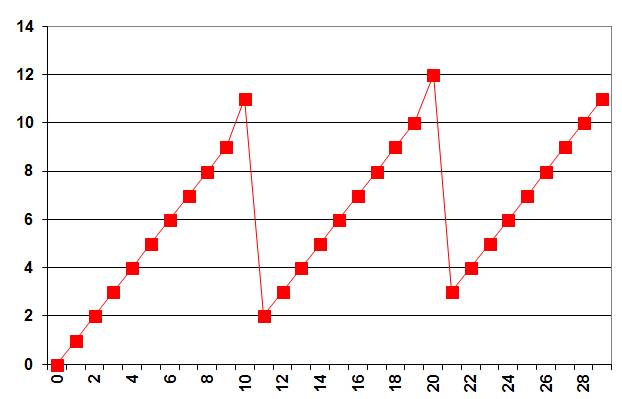
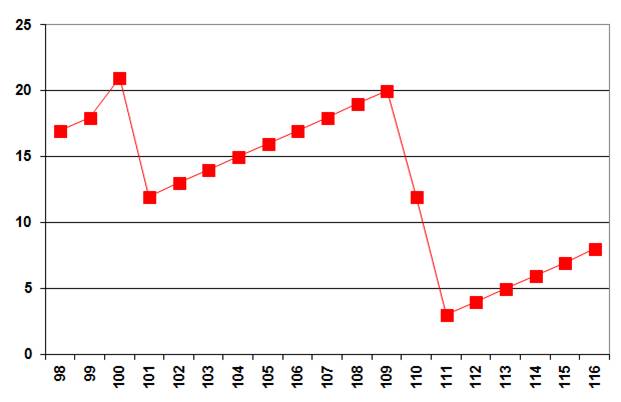
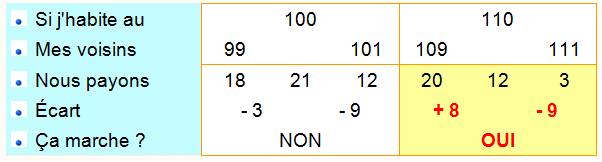
Il faut créer une nouveauté. Par exemple, l'arrivée des deux 0 du nombre 100. Voyons la courbe. Voyons les deux cas suivants Nous avons une solution! Conclusion Il s'agit d'un exemple de construction de devinettes mathématiques. Dans cet exemple, il faut chercher la configuration singulière. Les deux présentée (en 100 et 110) le sont. Celle en 100 (écarts -3 et -9) est proche de toutes celles en 10, 20 … (écarts -2 et -9) et elle est la même qu'en 200, 300 … Celle en 110 présente la configuration la plus inattendue (écarts + 8, -9) Prochaines configurations qui marchent

Énigme de la maison du maire
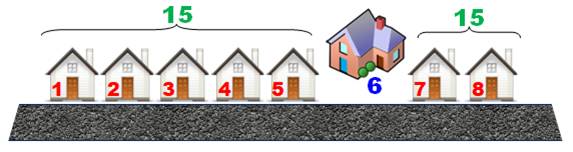
La maison du maire sur cette rue est au n°6. La somme des numéros de chaque côté est égale à 15.
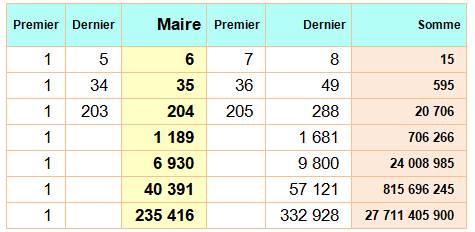
Quels sont les autres cas ?
Formule	Si a(0) = 1 et a(1) = 6, les suivants sont: a(n) = 6 x a(n – 1) – a(n – 2) Liste: 35, 204, 1189, 6930, 40391, 235416, 1372105, 7997214, 46611179, 271669860, 1583407981, 9228778026, 53789260175, 313506783024, 1827251437969, 10650001844790 …

Voir Suite et explications sur les sommes avant et après un nombre – Origine Ramanujan

Nombre racine carrée d'un triangulaire/ Brève 54-1070

Suite	Voir haut de page Filles (les trois) Les trois maisons Quel est le numéro de la villa? Énigmes classiques – logique – Découverte junior (diaporama)
Voir	Âge deviné Anniversaires Autres énigmes sur les âges Chaîne et hôtel Dates de naissance produit Élections Énigme des 5 hommes, 5 maisons … dite d'Einstein Énigme du sphinx Énigmes calculs Énigmes des filles Énigmes en poème Énigmes famille et probabilités Fortin d'Euler Garçons & Filles Huit fois mon âge Jeux – Index Logique – Index Paradoxes Roméo et Juliette
Site	OEIS A001109 – a(n)^2 is a triangular number: a(n) = 6*a(n-1) - a(n-2) with a(0)=0, a(1)=1.
Cette page	http://villemin.gerard.free.fr/Puzzle/EnigVila.htm