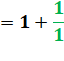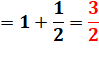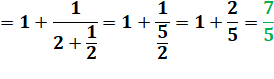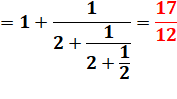|
|||||||||||||||||||||||||||||
![]()
|
Quel
est le numéro de la maison? Une
célèbre énigme qui semble simple; Pourtant sa résolution va nous embarquer
dans le monde des fractions
continues et des équations
de Pell. |
Voir
Problème de la maison du maire
Devinettes plus simples, de mise en jambe
|
Je
me rends au magasin et compte les maisons sur ma gauche: il y en a vingt.
Pour m'amuser, au retour, je compte celles sur la droite: il y en a vingt.
Combien de maisons ai-je compté en
tout? |
|
Deux
voisins face à face dans la rue constatent avec étonnement que leurs numéros
sont 33 et 66. En entrée de
rue, une des villas porte le numéro 1
et l'autre en face porte le numéro maximum N. À chaque villa d'un côté de la
rue fait face une villa de l'autre côté. Les
deux voisins se demandent s'ils peuvent calculer la quantité N de villas dans
la rue. |
|
|
|
|
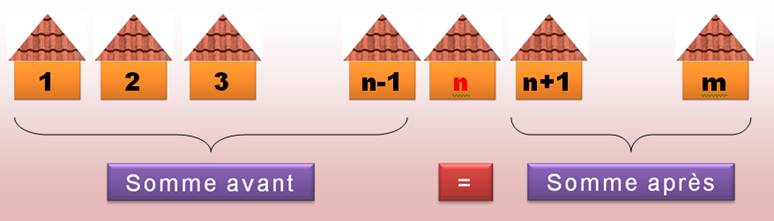
Problème
Une des maisons a un numéro
tel que la somme de tous les autres avant
dans la rue est égale à la somme de tous
les autres après dans la rue. Ce numéro est compris entre 50 et 500. Quel
est-il?
Exemple: Si n = 6 et m =
8 alors 1 + 2 + 3 + 4 + 5 = 15 = 7 + 8. Contexte · L'Indien P.C. Mahalanobis, compagnon de chambrée de Ramanujan à Whewell's Court, essayait de résoudre le problème figurant
sur un journal. Ramanujan écoute l'énoncé de l'énigme, tout en continuant à
faire frire ses légumes (il est végétalien) et affirme immédiatement qu'il
sait en trouver toutes les solutions avec l'aide de fractions continues.
Voici la solution que probablement Ramanujan avait en tête. · Pourquoi la ville de Louvain? En 1914, cette ville est embrasée et la
population torturée par les troupes allemande. Dans la presse, Louvain
devient le symbole d'un tournant de la civilisation vers la barbarie · Cette anecdote fut relatée dans le journal Strand de décembre 1914.
Une page y était consacrée aux énigmes. Cette fois le problème était
intitulé: "Puzzles at a Village Inn". Source: On
Ramanujan continued fractions par John Butcher. et le roman "Le
Comptable indien" par David Leavitt >>> |
|
|
|
|||
|
· Somme des entiers
jusqu'à n – 1, le numéro de la maison juste avant. |
Savant |
= ½ n (n – 1) |
|
|
· Somme des entiers après jusqu'à m, la dernière maison. |
Saprès |
= ½ m (m + 1) – ½ n (n – 1) – n |
|
|
· Égalité: |
½ n (n – 1) |
= ½ m (m + 1) – ½ n (n – 1) – n |
|
|
· En prenant le double: |
n (n – 1) |
= m (m + 1) – n (n – 1) – 2n |
|
|
· m d'un côté et n de l'autre. |
m (m + 1) |
= 2n (n – 1) + 2n |
|
|
· Calcul. |
m² + m |
= 2n² |
|
|
· Obtention de carrés: |
4m² + 4m + 1 4m² + 4m + 1 (2m + 1)² |
= 8n² + 1 = 2x4n² + 1 = 2 (2n)² + 1 |
|
|
· Ou, sous forme d'une équation: |
(2m + 1)² |
– 2 (2n)² – 1 = 0 |
|
|
· Sous forme générique: une équation de Pell. |
x² |
– 2 y² – 1 = 0
|
|
|
· Une solution facile à trouver: |
9 |
– 8 – 1 = 0 |
|
|
|
|||
|
· La solution fait appel à la fraction continue de racine
de 2 |
|
= [1, 2, 2, 2, …] |
|
|
Les réduites sont les fractions successives obtenues
en tronquant la fraction continue. Anglais: convergents. |
(1) |
|
|
|
(2) |
|
||
|
(3) |
|
||
|
(4) |
|
||
|
Nous reconnaissons la
solution: |
3² |
– 2 x 2² – 1 = 0 |
|
|
Solution suivante: |
17² |
– 2 x 12² – 1 = 0
= 289 – 2 x 144 + 1 |
|
|
Une fraction sur deux
fonctionne; les autres (en vert)
répondent à la même équation, mais en +1. |
x² |
– 2 y² + 1 = 0 |
|
|
|
|
|
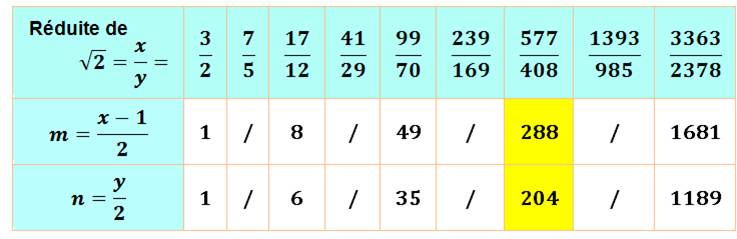
Seules les fractions à
dénominateur pair
conviennent:
Vérification 1 + 2 + 3 + … 203 = 203 x 204/2 = 20 706 205 + 206 + … 288 = 288 x 289/2 – 204 x 205/2 = 41 616 – 20 910 = 20 706. |
|
|
La maison dans la rue, ayant un numéro compris entre 50 et
150, telle que la somme de tous les numéros avant
est égale à la somme de tous les numéros après
est au numéro 204 pour 288 maisons dans la rue. Les nombres tels que la somme de tous les entiers précédents
soit égale à tous les entiers suivants sont 6 pour 8 au total, 35 sur 49, 204
sur 288, 1189 sur 1681, etc. Il existe une infinité de possibilités qui se
déduisent d'un calcul avec les réduites de racine de 2. |
Programmation de la recherche avec Maple
|
|
Commentaires Réinitialisation
générale. Boucle de recherche en
k. Demande de résolution
de l'équation indiquée qui détermine k pour égalité de part et d'autre de la
maison. Équation du deuxième degré qui possède deux
solutions. On ne garde que la
racine positive S[1], et seulement si c'est un nombre entier. En bleu, le résultat
du traitement. |
Voir
Problème de la maison du maire
/ Nombre racine carrée d'un triangulaire
Voir Programmation – Index
|
|
|
|
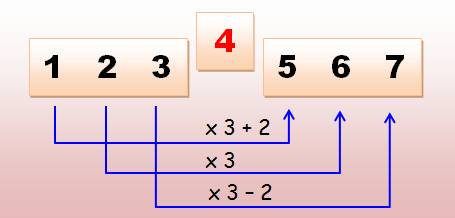
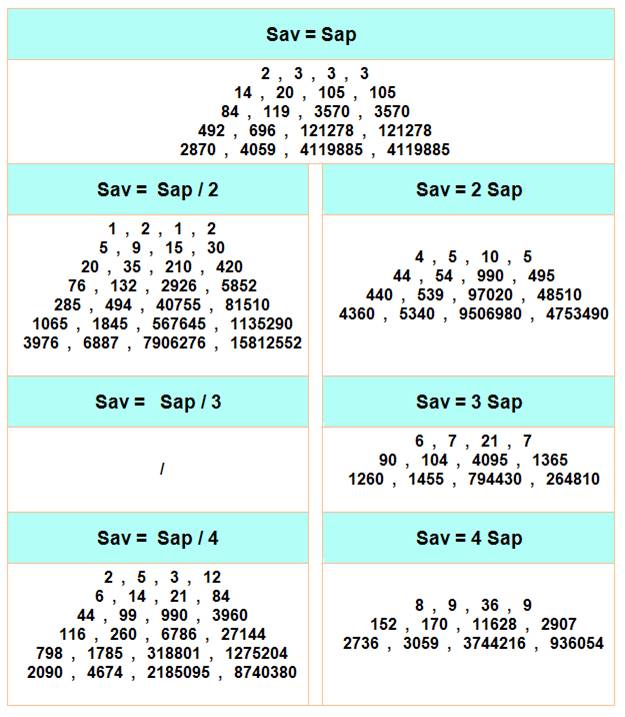
Nous sommes toujours dans le
cas où la somme d'un côté est égale à la somme de l'autre, tout en ignorant
le numéro central n. En tête du tableau, les cas
où la somme avant et la somme après sont égales. On trouve successivement n,
m, somme avant et somme après. Suivent les cas où la somme
après est une fraction ou un multiple de la somme d'avant. Exemple: n = 28 et m =
34, alors 1 + 2 + 3 + … + 27 = 378 et 29
+ 30 + … + 34 = 189 = 378 / 2.
Pour tout nombre n, il est possible de trouver une somme triple de
l'autre en prenant m = 2n – 1. Explication illustrée:
|
|
|
Si
j'ai compté quarante maisons, j'ai cependant compté deux fois les mêmes!
Donc, vingt maisons différentes. |
|
Deux
voisins face à face dans la rue constatent que leurs numéros sont 33 et 66.
En entrée de rue, une des villas porte
le numéro 1 et l'autre en face porte le numéro maximum N. À chaque villa d'un
côté de la rue fait face une villa de l'autre côté. Les
deux voisins se demandent s'ils peuvent calculer la quantité N de villas dans
la rue.
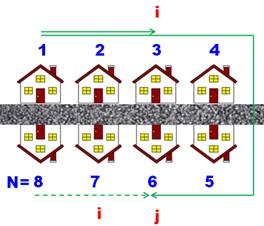
Prenons
un exemple simple avec huit villas. Les villas face à face portent les
numéros i et j. Et j = 9 – 3 = N + 1 – i. Autrement-dit:
N = i + j - 1 Dans
le cas proposé: N = 33 + 66 – 1 = 98. |
![]()
|
Voir |
|
|
Aussi |
·
Partage – Énigmes classiques · Problème de la maison du maire
(cas SAV = SAP) ·
Énigmes – Index
|
|
DicoNombre |
·
Nombre 14 ·
Nombre
84 |
|
· On
Ramanujan, continued fractions and interesting street number by John Butcher >>> · Ramblings
of a Ramdom Math Enthusaist par Karthik (texte de l'énigme en anglais) >>> · OEIS A001109
– a(n)^2 is a triangular number: a(n) = 6*a(n-1) - a(n-2) with a(0)=0,
a(1)=1. |
|
|
Livres |
· The
man who knew infinity par Robert Kanigel – Une référence! ·
Le
Comptable indien par David Leavitt -
La vie de Ramanujan auprès de Hardy, Littlewood et les autres …>>> |
|
Cette page |
![]()