|
||||||||||||||||||||||||||||
![]()
|
COMBIEN DE CONNAISSANCES ? Dans une assemblée, il existe
toujours deux personnes qui connaissent
le même nombre de personnes. |
|
PROBLÈME |
|
|
Données Dans une pièce,
il y n personnes. Affirmation Il existe
toujours deux personnes qui connaissent le même nombre de personnes (qui ont
le même nombre de connaissances). |
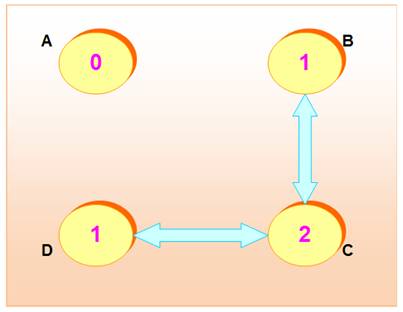
Exemple n
= 4 A ne connaît personne B connaît 1 personne C connaît 2 personnes D connaît 1 personne
|
|
Observation
Il est
nécessaire de visualiser la situation, tant cette affirmation n'est pas
évidente à admettre.
A priori, une personne présente ne
peut connaître que 3 personnes (il se connaît lui-même, mais cela n'est pas,
à proprement parler, une connaissance). Vous observez ici que, si l'une des
personnes ne connaît personne, alors l'une des autres personnes ne peut plus connaître
que deux personnes et non pas trois. |
Illustration (selon le libellé de
l'exemple ci-dessus)
C
a deux connaissances, ce qui implique
naturellement qu'il existe deux personnes qui connaissent C. |
|
Démonstration |
|
|
Nous allons
ranger les gens qui connaissent le même nombre de personnes dans le même
"tiroir". |
Je connais trois
personnes, je vais dans le tiroir
N°3. Je ne connais absolument
personne, je vais dans le tiroir
N°0. |
|
Une personne va
dans le tiroir i si elle connaît i personnes. |
n tiroirs numérotés de 0
à n-1 pour ranger n catégories de personnes. |
||||
|
Si vous vous reportez
à l'illustration, vous pourrez facilement constatez que deux cas sont incompatibles. Si personne ne se
connaît, alors ces gens ne peuvent pas, à la fois, tous se connaître À
l'inverse, s'ils se connaissent tous, alors il n'y a personne pour ne connaître
personne. |
S'il y a quelqu'un en 0,
il n'y a personne en n-1 S'il y a quelqu'un en
n-1, il n'y a personne en 0 Les deux tiroirs sont
exclusifs n - 1 tiroirs
possibles seulement. |
|
Cette constatation
nous amène à déduire qu'il n'y a, de fait, que n-1 tiroirs
disponibles pour ranger nos n catégories de personnes. |
Par le principe des
tiroirs, ayant n catégories de personnes à ranger dans n-1 tiroirs, alors deux personnes, au moins,
sont forcément dans le même tiroir, ou autrement dit deux personnes, au moins, ont le même nombre de
connaissances. |
![]()
|
Suite |
|
|
Voir |
|
|
Aussi |
|
|
Cette page |
http://villemin.gerard.free.fr/aMaths/Denombre/Tiroir/TiroirCo.htm |
![]()