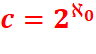|
|||||||||||||||||||||||||||||||||||
![]()
|
COMPTER
OU DÉNOMBRER la quantité des nombres entiers, rationnels ou réels
|
|
|
|||
|
0, 1, 2, 3, 4, …, 456 213, … |
|
Infinité |
|
|
Entiers
pairs 0, 2, 4,
6, …, 64204, … |
|
Infinité |
|
|
Entiers
impairs 1, 2, 3,
5, …, 64203, … |
|
Infinité |
|
|
Entiers
premiers 2, 3, 5,
7, 11, 13, … |
|
Infinité |
|
|
1!, 2!,
3!, … |
|
Infinité |
|
|
1, 3, 6,
10, … |
|
Infinité |
|
|
Etc. |
|
|
|
|
|
|||
|
Entiers |
|
|
|
|
Entiers pairs |
|
|
|
|
Autres |
|
|
|
|
Lorsque les éléments
de deux ensembles peuvent être mis en correspondance terme à terme, on dit
qu'ils sont en bijection.
|
Voir
DicoMots Maths / Bijection
|
|
||
|
|
Infinité |
|
|
|
Infinité Infinité |
|
|
|
|
|
|
|
||
Bilan
|
Il y a une
infinité de nombres entiers et une infinité de nombres rationnels
(fractions). Ce sont deux infinités de même type, dite dénombrable. C'est le plus
petit des ensembles infinis. Sa taille est appelée Aleph
zéro ( C'est le "nombre
infini" des entiers. C'est
le cardinal de l'ensemble C'est
le cardinal de l'ensemble |
Voir
Histoire de la notation / Ensembles
de nombres
Arithmétique
singulière
|
Si on ajoute 1
à une infinité, cela donne une infinité:
Si on ajoute
une infinité à une infinité (les pairs plus
les impairs, par exemple): |
Voir
L'hôtel de Hilbert / Arithmétique avec Aleph
|
|
||
|
Affirmation Il y a plus de nombres réels que de nombres rationnels. Il y en a une
infinité non dénombrable. Principe
de la démonstration |
||
|
|
Infinité |
|
|
|
Encore plus |
|
|
|
|
|
|
Démonstration |
|
|
Hypothèse
Les valeurs données
à droite sont illustratives. |
N1
= 0, 123… N2 = 0, 324… N3 = 0, 567… … Nn = 0, 754…a… … |
|
Formation
d'un nouveau nombre
On peut prendre
n'importe lequel, sauf 1.
|
N
= 0, … N
= 0, 2… N
= 0, 23… N
= 0, 238… N
= 0, 238…b… |
|
Nouveau
nombre
|
N
= Nk |
|
Oui,
mais
|
k
k
k
|
|
Conclusion
|
|
Voir Diagonale de
Cantor
|
Il a au moins
deux niveaux d'infinis:
Quelle est la différence
entre ces deux types d'infinis ? Est-ce qu'il y quelque chose au-delà ? Et, entre les deux ? Quid de |
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()