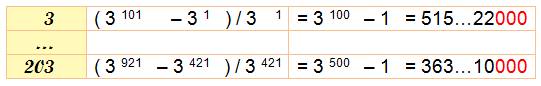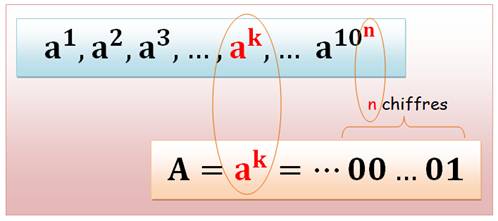
NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 26/12/2016 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique
	Dénombrement
Débutants Général	Principe des TIROIRS			Glossaire Général
INDEX Dénombrement	Débutant	Exemples	Connaissances	Nb en 00 ..01
	Introduction	Divisibilité 10	Divisibilité 2n	Divisibilité n
		Sommaire de cette page >>> Approche >>> Puissances de 10 >>> Généralisation >>> Démonstration >>> Tables des nombres en 00…01

NOMBRES en …00…01

Certains nombres (A) ayant n chiffres finaux en 00…01, sont des puissances entières.

Parmi les puissances A = a^k jusqu'à k = 10ⁿ, il existe toujours un nombre A terminé de n chiffres en 00…01, sauf si a n'est pas premier avec 10ⁿ.

Exemples

3 ²⁰ = 3486784401

57¹⁰⁰ = 3867…3900001

APPROCHE
Mise en place Prenons un nombre a = 3, par exemple, premier avec 10. Ses puissances successives jusqu'à 10. Et les restes de la division par 10 de ces nombres. Remarque fondamentale Le nombre a étant premier avec 10, aucun reste n'est nul. Au plus, il y a 9 types de restes pour les 10 restes que nous cherchons. Par le principe des tiroirs, au moins deux restes sont identiques.
Observations Choisissons deux de ces nombres ayant le même reste lorsque divisé par 10. Leur différence est divisible par 10. Mise en facteur. Or 3 a été choisi étant premier avec 10. c'est donc le deuxième facteur qui est divisible par 10. Et, en effet:

Voir Modulo

Conclusions

Pour tout nombre a premier avec 10,
il existe une puissance de a diminuée de 1 divisible par 10.

Pour tout nombre a premier avec 10ⁿ,
il existe une puissance de a diminuée de 1 divisible par 10ⁿ.

Pour tout nombre a premier avec N,
il existe une puissance de a diminuée de 1 divisible par N.

Si le PGCD de a et N est égal à 1, alors il existe un entier k tel que N divise la puissance k de a.

Exemple avec 13

Le nombre a = 3 est premier avec 13. Nous avons par exemple:
Avec le même reste égal à 3 (3¹⁰ – 3⁷) / 3⁷ = 3³ – 1 = 27 – 1 = 6 = 2 x 13.

Avec le même reste égal à 9 (3⁵ – 3²) / 3² = 3³ – 1 = 27 – 1 = 6 = 2 x 13.

Exemple avec 100

Le nombre a = 3 est premier avec 100. Nous avons par exemple:
3²¹ – 3¹ = 3²⁰ – 1 = 100 x 34 867 844.

Cette puissance 21 étant la plus petite répondant aux critères.

Voir Unités des puissances

Puissances de 10

Avec 3^k et k = 100 = 10^2 Nous recherchons les puissances de 3 qui ont le même reste en les divisant par 100 (colonne jaune). La différence entre ces puissances de même reste est divisée par la puissance commune. Cette puissance diminuée de 1 est divisible par 100. On peut dire aussi que 3^20 est un nombre qui se termine par 01 Avec 3^k et k = 1000 = 10^3 Même principe avec 1000. Voici deux exemples On peut dire aussi que 3^100 est un nombre N qui se termine par 001 avec Compte tenu des valeurs élevées des puissances, seuls quelques nombres en …001 sont atteints par une telle relation.

Généralisation
Affirmation Soit un nombre a premier avec 10^n. Il existe une puissance k de ce nombre égale à 1 modulo 10^n. N =…001 = a^k	Exemples (cf. table ci-dessus) N = 2 401 = 7^4 = 49^2 N = 3 486 784 401 = 9^10 = 3^20 N = 25 937 424 601= 11^10

Démonstration
On considère les puissances successives de a jusqu'a une puissance de 10 choisie.	a, a^2, a^3, …, a^D avec D = 10^n
On divise chacune par 10^n et on ne garde que le reste de la division.	ri = a^i mod 10^n
Or a est premier avec 10^n. Notamment, il n'est pas terminé par 0.	a et ses puissances, divisés par D, la puissance de 10, ne donnent jamais 0 comme reste.
En conséquence, la quantité de restes est égale au total des possibilités moins une.	(10^n – 1) restes possibles pour 10^n nombres.
Selon le principe des tiroirs, ont déduit que deux nombres ont même reste.	a^i et a^j ont même reste lorsque divisés par 10^n
Si deux nombres donnent le même reste lorsqu'ils sont divisés par un nombre, leur différence est divisible par ce nombre.	a^i – a^j est divisible par 10^n On écrit aussi 10^n a^i – a^j
Nous parlons des puissances successives de a. Prenons a^j la plus grande, elle contient a^i comme facteur.	a^j = a^i (a ^j – i – 1)
Divisibilité réécrite.	10^n a^i (a ^j – i – 1)
On sait que a et ses puissances sont premiers avec 10 et ses puissances. Si 10^n ne divise pas l'un des facteurs, il divise l'autre. Soit une nouvelle version de la divisibilité.	10^n (a ^j – i – 1)
L'expression entre parenthèse est égale à un certain nombre de fois 10^n.	a ^j – i – 1 = q . 10^n
Simple changement de côté pour le 1.	a ^j – i = q . 10^n + 1
Les n chiffres de droite de a^j-1 sont des zéros sauf le dernier qui est 1.	a ^j – i = … 000…01

Suite	Tables des nombres en 00…01 Divisibilité par 2n
Voir	Coïncidences Dénombrement et tiroirs Sudoku Exemples d'applications
Aussi	Compter Jeux – Index
Cette page	http://villemin.gerard.free.fr/aMaths/Denombre/Tiroir/TiroirZU.htm