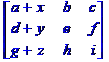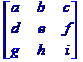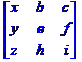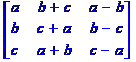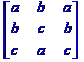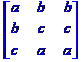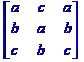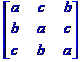|
|||||||||||||||||||||||||||||||||||||||||||||
![]()
|
MATRICES – Déterminants (2/2)
|
Voir Débutants /
Novices
|
|
|||||||||||
|
le
déterminant est la somme des déterminants des matrices obtenues |
Décomposition
en sommes Det = + x.e.i - x.f.h + y.c.h - y.b.i + z.b.f - z.c.e |
||||||||||
|
Exemple de calcul
Détermin Qui est le détermin |
|||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
SUITE |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/aMaths/Outils/Matrice/Determ2.htm |
![]()