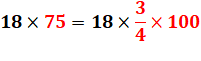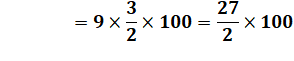|
|||||||||||||||||||||||||||||
![]()
|
Exercices typiques de calculs de niveau école primaire De nombreux élèves
voudraient mieux comprendre la résolution des problèmes qui leur sont présentés.
Ces pages donnent la solution classique (directe) des problèmes, suivies
d'une explication illustrée et détaillée. Le but étant de bien suivre le
mécanisme du raisonnement et de le visualiser pour être capable de
l'appliquer à d'autres problèmes semblables. |
|
|
||
|
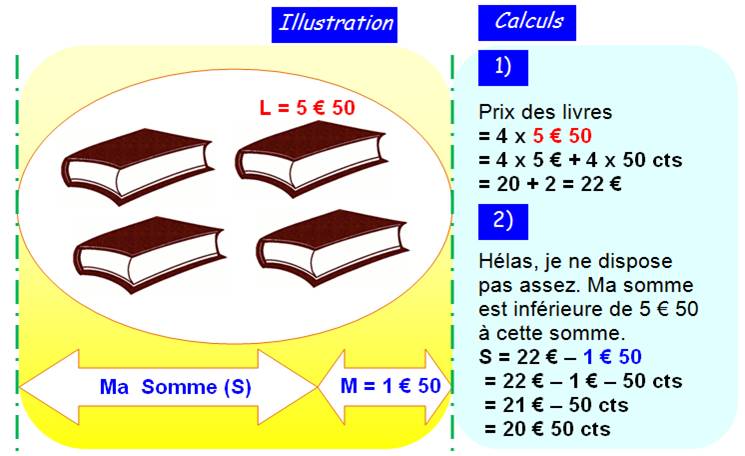
Problème Je dispose d'une certaine
somme. Unité Je me souviens
que 1 € 50 veut dire un euro et cinquante centimes. Je peux
aussi l'écrire: 1,50 euro et le
traiter comme un nombre
décimal (un nombre à virgule). |
Solution directe Ma somme est égale au prix
des quatre livres diminuée de ce qui me manque S = 4 x 5,50 – 1,50 = 22 –
1,5 = 20,5 S = 20 euros et 50 centimes. |
|
|
Solution détaillée et illustrée
|
||
|
|
||
|
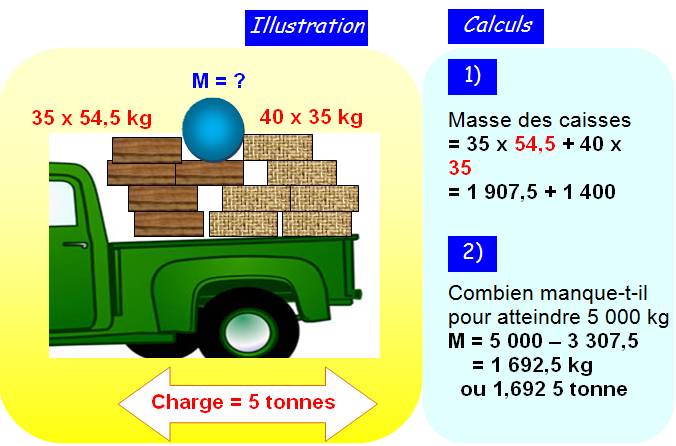
Problème Le chargement d'un camion est composé de 35 caisses
pesant chacune 54,5 kg et de 40 caisses pesant 35 kg. Quelle masse doit-on ajouter
pour que la charge de ce camion atteigne 5 tonnes? Notes sur les unités
|
Solution directe Ici, la charge veut dire la masse (ou dans le langage
populaire, le poids) La charge à ajouter est
égale à la charge demandée diminuée de la masse des caisses déjà mises sur le
camion. M = 5 000 – (35 x 54,5 + 40
x 35) = 5 000 – (1 907,5 + 1 400) = 5 000 – 3 307,5 = 1
692,5 kg |
|
|
Calcul de l'ordre de grandeur Opération mentale nécessaire pour
valider le résultat trouvé.
|
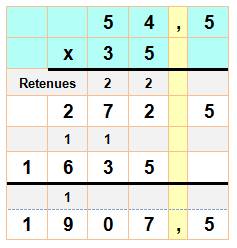
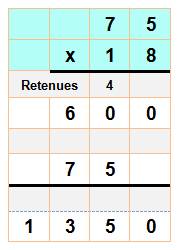
Rappel : comment poser la multiplication
Voir Multiplication |
|
|
Solution détaillée et illustrée
|
||
|
|
||
|
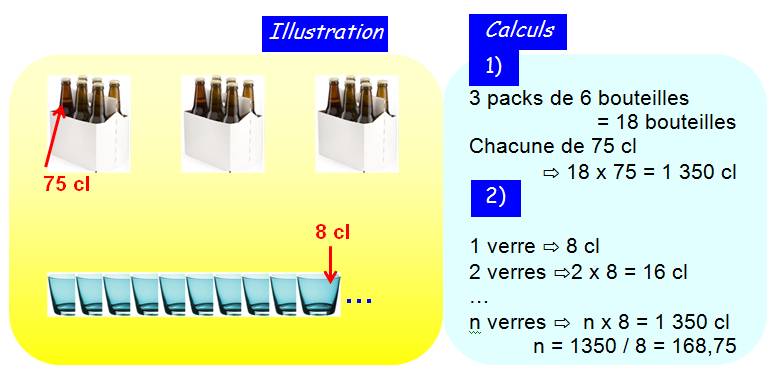
Problème Combien remplira-t-on de verres de 8 cl chacun avec 3 packs
de 6 bouteilles, chaque bouteille contenant 75 cl ? Unité L'abréviation officielle de litre est un petit l, que
l'on peut écrire grand L, pour le rendre plus lisible. Par contre, avec un préfixe,
on maintient le petit l: cl pour centilitre et non cL. |
Solution directe Quantité de liquide: 3 x 6 x 75 = 18 x 75 = 1 350
cl Quantité de verres remplis: 1 350 / 8 = 168,75 verres Soit 168 verres pleins Le suivant est plein aux trois-quarts |
|
|
Multiplication avec astuce (fraction)
Voir
Fraction |
Multiplication posée
|
|
|
Solution détaillée et illustrée
|
||
|
|
||
|
Problème Un cycliste s’entraîne
progressivement. Il fait une petite sortie le
lundi, puis, du mardi au
vendredi, il double chaque jour la distance parcourue la veille. Le samedi, il réduit de
moitié la distance parcourue le vendredi et se repose le dimanche. En une semaine, le cycliste
fait au total 195 km. Quelle distance a-t-il
parcourue le mercredi? |
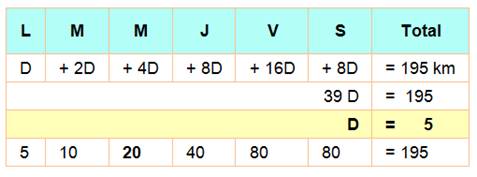
Solution Le lundi il parcourt la
distance L. Mardi: 2L. Etc. Voici le bilan en tableau
Le mercredi, il parcourt 20 km. |
|
![]()
|
Suite |
|
|
Voir |
|
|
Livre |
|
|
Site |
|
|
Cette page |
http://villemin.gerard.free.fr/aMaths/Primaire/Calculs/EXO01.htm |
![]()