|
|||||||||||||||||||||||||||||
![]()
|
Exercices typiques de logique Comment résoudre un problème en faisant des suppositions De nombreux élèves
voudraient mieux comprendre la résolution des problèmes qui leur sont présentés.
Ces pages donnent la solution classique (directe) des problèmes, suivies
d'une explication illustrée et détaillée. Le but étant de bien suivre le
mécanisme du raisonnement et de le visualiser pour être capable de
l'appliquer à d'autres problèmes semblables. |
|
|
||
|
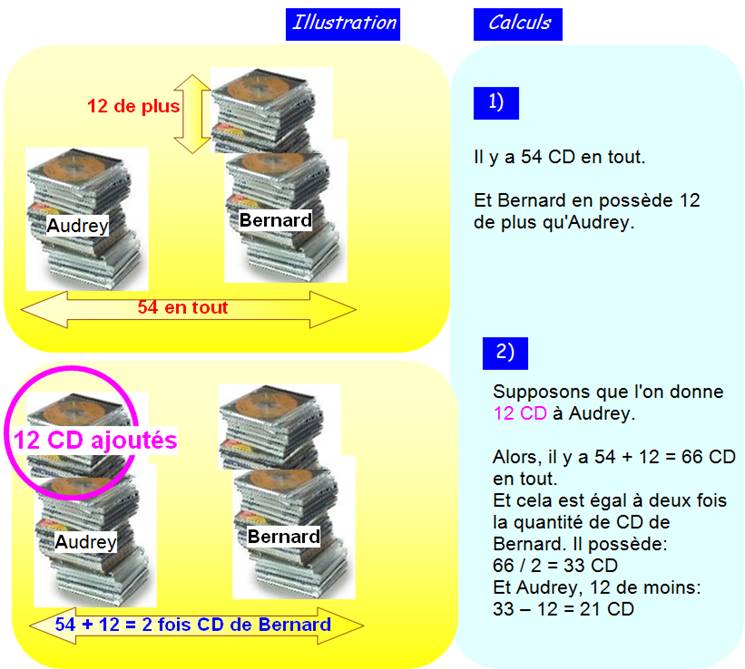
Problème Audrey et Bernard comptent
leurs CD. Ils en ont 54 à eux deux. Audrey en a 12 de moins que
Bernard. Combien possèdent-ils de CD
chacun? Solution par raisonnement (supposition). Si Audrey avait le même
nombre de CD que Bernard, il y en aurait 12 de
plus 54 + 12 = 66 C'est deux fois la quantité
de CD de Bernard 66 / 2 = 33 CD Et Audrey en a 12 de moins: 33 – 12 = 21 CD |
Solution méthodique (équations) Il faut trouver deux nombres
avec une somme de 54. A + B = 54 Bernard a le même nombre de
CD qu'Audrey plus 12. B = A + 12 En mettant les CD de Bernard
dans la somme (on remplace B par sa valeur): A + A + 12 = 54 2A + 12 = 54 Je retire 12 de chaque côté: 2A + 12 – 12
= 54 – 12 2A = 42 A = 21 CD Je calcule B: B = A + 12 = 21 +
12 = 33 CD |
|
|
Solution détaillée et illustrée
|
||
|
|
||
|
Problème Le Petit Poucet s’amuse dans
un escalier. Il a 55 cailloux dans la poche de son pantalon.
Et ainsi de suite… Sur
quelle marche pose-t-il le dernier caillou ? |
Solution par dénombrement (en comptant) La somme des cailloux va
croissant de cette manière: M1: 1 M2: 1 + 2 = 3 M3: 1 + 2 + 3 = 6 M4: 1 + 2 + 3 + 4 = 10 M5: 1 + 2 + 3 + 4 + 5 = 15 M6: 1 + 2 + 3 + …+ 6 = 21 M7: 1 + 2 + 3 + …+ 7 = 28 M8: 1 + 2 + 3 + …+ 8 = 36 M9: 1 + 2 + 3 + …+ 9 = 45 M10: 1 + 2 + 3 + …+ 10 = 55 Voir Somme des nombres de 1 à 100 |
|
|
Solution astucieuse Supposons que pendant que le
Petit Poucet dépose ses cailloux, son frère part du haut des escaliers et
fait la même chose jusqu'en bas. Imaginons qu'il y a 10
marches. Si ce n'est pas cela on recommencera avec un autre nombre. Sur la première marche il y
aura 1 + 10 = 11 cailloux; sur la deuxième, il y aura 2 + 9 = 11 cailloux. En
effet, il y aura la même quantité de cailloux sur les 10 marches. Il y en a 10 x 11 = 110 en tout Comme chaque garçon a déposé
autant de cailloux, Le Petit Poucet en a déposé: 110 / 2 = 55. Bravo! C'est
le nombre cherché. Illustration |
||
![]()
|
Suite |
|
|
Voir |
|
|
Livre |
|
|
Site |
|
|
Cette page |
http://villemin.gerard.free.fr/aMaths/Primaire/Logique/LOEXO01.htm |
![]()