équations débutants

NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 02/08/2019 Orientation générale DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique Brèves de Maths
	Algèbre
Débutants Général	ÉQUATIONS			Glossaire Équations 2^e degré
INDEX Équations Algèbre	Débutants	Généralités	Techniques de base
	Premier degré	Deuxième degré	Troisième degré
	Deux inconnues	Deux équations ou plus
	Page lisible dès 9-10 ans	Sommaire de cette page >>> En équilibre >>> En plus >>> En moins >>> En paquets >>> En résumé >>> Entre parenthèses >>> Français et anglais >>> Amusements

ÉQUATIONS – Débutants

Je vous vois en train de dire:

"Autant dire tout de suite que je me mélange les pinceaux avec les signes, les parenthèses et les côtés de l'équation. Je ne me souviens jamais dans quel ordre il faut faire. C'est du chinois pour moi …"

Voyons cela en partant du début le plus simplement possible. Méthode visuelle qui permet de bien ancrer les principes une fois pour toute. Cette page est abordable comme initiation avant le collège.

Pour commencer voir: Initiations aux Opérations arithmétiques / Tracas de calculs / Cours de 5^e

Devinette

Cette balance est en équilibre.

Quel est le poids d'une seule bouteille d'eau?

En retirant une bouteille de chaque côté, on ne modifie pas l'équilibre.

Donc deux bouteilles pèsent donc 2 kg, et une bouteille pèse 1 kg.

Si vous avez compris cette énigme, vous avez compris comment résoudre les équations!

Voir Énigmes de pesée

EN ÉQUILIBRE

Prenons des objets ayant chacun une masse déterminée:

Cube bleu pèse 10

Cylindre jaune pèse 5

Triangle brun pèse 1

La balance est en équilibre si chacun des plateaux porte la même masse totale.

Résoudre une équation consiste à faire des manipulations avec ces objets en respectant l'équilibre de la balance.

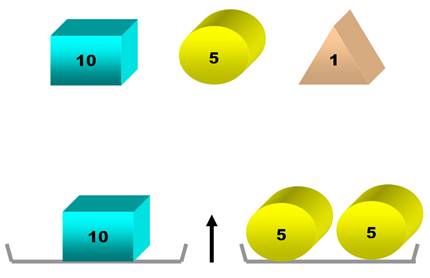
Cette balance montre l'équilibre.

Normal! 10 = 5 + 5

Facile, non? Le reste n'est pas plus compliqué …

EN PLUS

Soit l'équation suivante x + 5 = 10
Traduisons en objets sur les plateaux

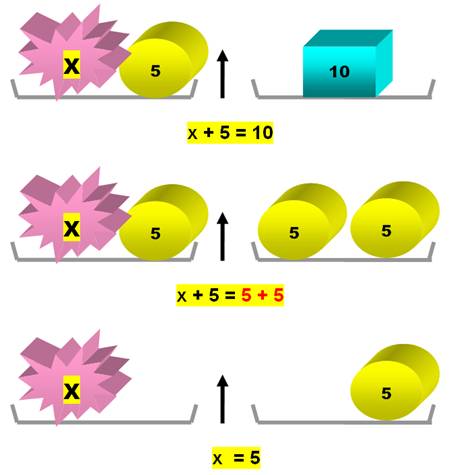
L'objet x est un parfait inconnu.

Nous ne savons ce qu'il pèse!

En se mesurant aux autres, il va se trahir

Vous ne verrez pas d'inconvénient à remplacer la masse 10 par deux masses de 5 chacune. Car 5 + 5 = 10.

La règle des deux mains dit simplement que:

si j'ajoute la même masse de chaque côté l'équilibre est maintenu.

Ou inversement:

si je retire la même masse de chaque côté l'équilibre est maintenu.

Règle des deux mains:

Ce que fait la main gauche, doit aussi être fait par la main droite pour conserver le parfait équilibre.

Avec un peu d'habitude

EN MOINS

Soit l'équation suivante x – 5 = 10.
Traduisons en objets sur les plateaux. Le ballon jaune est tel qu'il tire le plateau gauche vers le haut avec une force de 5

Autrement dit: l'objet X est allégé de 5 sur le plateau.

Appliquons la règle des deux mains en ajoutant 5 sur chaque plateau. L'équilibre est bien sûr maintenu.

Observons le plateau de gauche ci-contre:

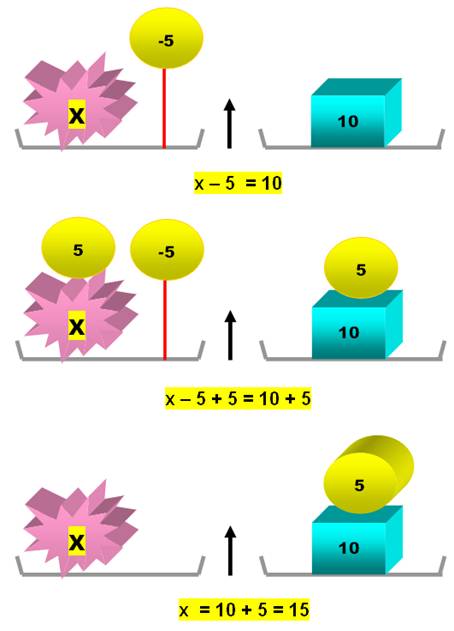
Un objet pèse 5 (vers le bas);

Un autre allège de 5 (vers le haut;

Les deux se neutralisent.

Il est possible de les retirer sans modifier l'équilibre.

Bilan: oubliez le dessin du milieu et observez le premier et le dernier. Le ballon 5 à gauche est devenu une masse de 5 à droite.

- 5 à gauche vaut +5 à droite.

Règle des deux mains:

Ce que fait la main gauche, doit aussi être fait par la main droite pour conserver le parfait équilibre.

Application aux équations:

Un PLUS de gauche se transforme en un MOINS à droite et inversement.

Oui, le signe moins ne doit plus effrayer.

Il se transforme en signe plus en le passant de l'autre côté.

Avec l'habitude

EN PAQUETS

Soit l'équation suivante 4.x = 20.

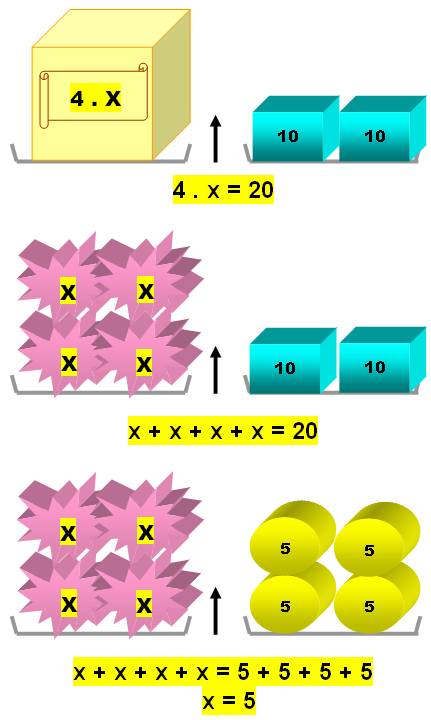
Traduisons en objets sur les plateaux. L'objet 4.x est un paquet. Qu'y a-t-il dans ce paquet?

Vous, vous savez évidemment ce qui est dans ce paquet. Ce sont quatre objets du type x. Ils pèsent quatre fois la masse x sur le plateau.

En bref, le plateau de gauche comporte 4 objets

L'astuce consiste à former autant d'objets de chaque côté. Alors chaque objet d'un côté trouve son équivalent de l'autre côté. Et, bien entendu, chacun pèse la même chose.

Bilan: pour passer de 4 objets à un seul, vous avez sans doute reconnu le principe d'une division par 4.

Note sur la notation

Nous conserverons pour le moment un point pour signifier la multiplication. Le signe X n'est pas utilisé car il se confondrait avec l'inconnue x. Avec de l'habitude, et lorsqu'il n'y a pas de confusion possible le point de la multiplication sera éliminé 4.x deviendra 4x.

Règle des paquets:

Les paquets formés à gauche doivent correspondre aux paquets formés à droite.

Application aux équations:

Éliminer MULTIPLICATION à gauche implique une DIVISION à droite et inversement.

Bien sûr par le même nombre et à condition que ce nombre ne soit pas 0.

Avec l'habitude

EN RÉSUMÉ – Ce que nous avons appris

RÈGLE DES DEUX MAINS

On peut ajouter ou retrancher la même quantité sur chacun des plateaux sans modifier l'équilibre.

RÈGLE DES PAQUETS

Si un équilibre est obtenu par la même quantité de paquets sur chaque plateau de la balance:

L'équilibre demeure si on conserve un seul des paquets de chaque côté (division).

L'équilibre subsiste si on place k fois plus de paquets de chaque côté (multiplication).

On peut ajouter ou retrancher la même quantité de chaque côté de l'équation sans modifier l'égalité

2.x – 6 = 0

2.x – 6 + 6 = 0 + 6

2.x = 6

On peut multiplier ou diviser chaque côté de l'équation par le même facteur sans modifier l'égalité.
Attention: la division par 0 est interdite.

2.x = 6

2.x /2 = 6 /2

x = 3

Anglais: division property of equality: what you divide by on one side of the equal sign you must divide by on the other (in order for the equality to be preserved). If a = b then a/c = b/c (as long as c is not zero).

ENTRE PARENTHÈSES – Colisage

Comment s'y prendre avec cette équation?
Ce qui est entre parenthèse doit être considéré comme un COLIS, comme un tout. Il n'est pas possible de l'ouvrir sans précaution pour conserver son intégrité.

Ici nous avons deux fois le COLIS.

Nous allons utiliser la règle des paquets (multiplication / division) tout en remarquant que 10 est en fait équivalent à 2 paquets de 5

Nous pouvons ouvrir le paquet (enlever les parenthèses) car ce paquet est isolé.

Et finalement, nous pouvons appliquer la règle des deux mains, en ajoutant 2. Le -2 devient +2 de l'autre côté de l'équation.

2 . ( x – 2 )

2 . (x – 2) /2

( x – 2 )

x – 2

x – 2 + 2

= 10

= 2 . 5

= 2 . 5 /2

= 5

= 5 + 2

= 7

Voir Utilisation des parenthèses

Français et anglais

En français, on énonce complètement les propriétés de résolution des équations. Par exemple:

"Une égalité reste vraie si on multiplie ou si on divise ses deux membres

par un même nombre non nul"

Les Anglo-Saxons nomment ces propriétés:

Addition Property of Equality

Subtraction Property of Equality

Multiplication Property of Equality

Division Property of Equality

Substitution Property of Equality

En français, on pourrait utiliser le vocable général:

"Propriété d'égalité dans les équations" pour englober tous les cas.

Les Canadiens ne semblent pas avoir traduit ces termes (selon mes recherches).

Pour mémoire: Al Khawarizmi utilisait le terme al jabr pour l'addition et muqabala pour la soustraction.

Amusements

Panique! On vous embrouille l'esprit …
On trouve ces équations sur Internet et on vous demande de les résoudre; alors si vous y arriver, vous êtes élu au rang des génies. Il s'agit d'une devinette, et il y a une astuce "colossale". Futée, mais qui peut perturber le novice qui cherche à avoir les idées claires quant à la résolution des équations. Les profs jusqu'en classe de troisième le savent. La malice consiste à galvauder le signe égal qui prend, ici, une signification inhabituelle. Pour éviter d'embrouiller l'esprit des plus jeunes, il vaudrait mieux remplacer le signe égal par un symbole comme ou encore mieux qui indique une correspondance. Quelle est l'astuce? Chaque ligne contient une multiplication: 8 x 2 = 16, puis une addition: 8 + 2 = 10, et enfin une soustraction: 8 – 2 = 6 Nombres mis bout à bout (concaténés): 16106. La division était plus difficile à caser!
Dans le même esprit où le signe égal doit être interprété autrement. On devrait dire: *Trouvez une équation avec les nombres (1, 4 et 5); équation qui se répète de la même manière sur les lignes suivantes.* Ici, avec les nombres (a, b et c), l'équation à trouver est:
L'algorithme sur chaque ligne consiste simplement à ajouter les deux nombres et à les multiplier par 3. Exemple (1 et 3) => (1 + 3) x 3 = 12 Solution (4 et 20) => (4 + 20) x 3 = 72.
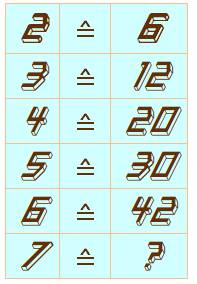
Celle-ci est bien posée avec un symbole "égal avec chapeau" qui veut dire: si 2 correspond à 6, alors 7 correspond à quel nombre? Ici la logique consiste à multiplier le nombre de gauche (n) par son prédécesseur (n-1) pour obtenir le nombre de droite: 2 x 3 = 6; 3 x 4 = 20; etc. Sachant que les nombres de gauche sont incrémentés (+1) à chaque nouvelle ligne. Réponse: 7 x 8 = 56 Bonus: notez que chaque résultat est le carré du nombre suivant moins lui-même: 3² – 3 = 9 – 3 = 6; 6² - 6 = 36 – 6 = 30 ; etc.