|
Édition du: 04/06/2023 |
|
INDEX |
Nombres et théorème de RAMSEY |
|||
|
|
||||
Faites un double-clic pour un retour en haut de page
![]()
|
Nombre de Ramsey R(3,3) = 6 Ce nombre est le
plus simple à déterminer. |
||
|
|
Sommaire de cette page >>> Approche >>> Démonstration avec les graphes >>> Jeux avec papier crayon – Jeu de Sim |
Débutants Glossaire |
|
C'est le nombre le plus facile à déterminer, même
intuitivement. |
R(3, 3) = 6 |
|
|
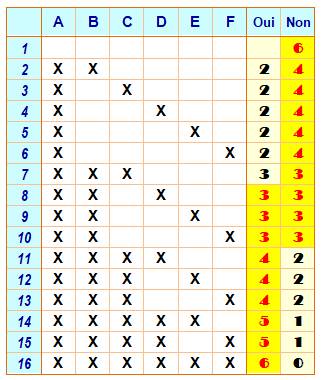
Exemple d'application concret Il faut et il suffit de rassembler six
personnes pour que, au moins, trois
se connaissent ou que trois ne se
connaissent pas. On dit que le nombre de Ramsey est 6 pour ce cas {3, 3}. On note R(3, 3) = 6. Tableau Six personnes A, B, C, D, E et F. Seize cas de connaissances symbolisés par les croix dans les colonnes Les deux dernières colonnes comptabilisent la quantité de connaissances
ou non La couleur jaune foncée montre qu'il existe toujours trois personnes,
ou plus, qui se connaissent ou qui ne se connaissent pas. |
|
|
|
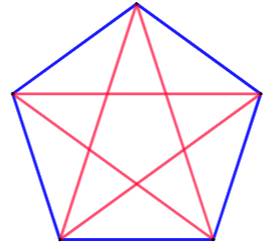
Cinq sommets Le dessin montre qu'il est possible de colorier
le pentagone complet avec deux couleurs sans créer de triangle. Notez bien que les
triangles devraient être construits sur les sommets de l'hexagone. Les
triangles rouges de la figure ne comptent pas. Le nombre de Ramsey est supérieur à 5. |
Existence d'un tracé complet
avec deux couleurs sans formation d'un triangle. |
|
|
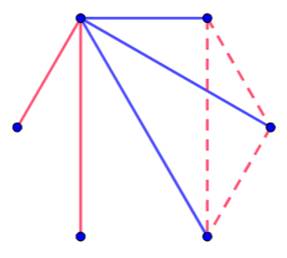
Six sommets Parmi les cinq arêtes issues d'un sommet donné,
et selon le principe des tiroirs, trois sont d'une couleur et deux de
l'autre. La figure donne un exemple. Avec les trois bleus, une arête supplémentaire
(pointillé) doit être rouge pour ne pas créer de triangle bleu. Comme c'est obligatoire pour les trois cas, on forme
nécessairement un triangle rouge. Le raisonnement vaut si on échange les couleurs. En coloriant le graphe complet à six sommets (R6),
on trouve inévitablement un triangle monochrome Le nombre de Ramsey (3, 3), supérieur à 5, est donc 6. En fait, il a été prouvé qu'il existe toujours deux triangles monochromatiques. |
Quelque soit le choix de la
couleur, le tracé en pointillé induit inévitablement un triangle monochrome. |
|
|
|
||
|
Jeux avec six points On peut imaginer un jeu à deux. Six points sont
dessinés en un cercle approximatif. Chaque joueur dessine un trait rouge pour
l'un et bleu pour l'autre. Le premier qui dessine un triangle de sa couleur
a perdu. |
Évidemment, le jeu ne peut pas se terminer par un
match nul car R(3, 3) = 6. |
|
Haut de page (ou
double-clic)
![]()
|
Retour |
|
|
|
Suite |
|
|
|
Voir |
|
|
|
Cette page |
http://villemin.gerard.free.fr/aMaths/Topologi/aaaRamse/R33.htm
|
|