|
Édition du: 03/06/2023 |
|
INDEX |
Nombres et théorème de RAMSEY |
|||
|
|
||||
Faites un double-clic pour un retour en haut de page
![]()
|
Nombre de RAMSEY R(3,5) |
||
|
|
Sommaire de cette page >>> R(3, 5) – Borne inférieure >>> R(3, 5) – Borne supérieure >>> Assemblée |
Débutants Glossaire |
|
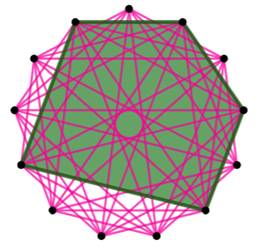
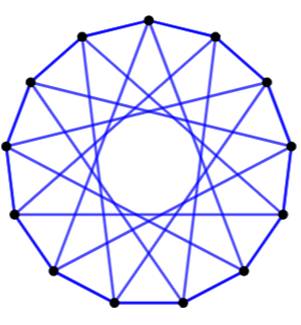
Borne inférieure Avec 13 sommets, il est possible de colorier le
graphe complet avec deux couleurs sans jamais créer un triangle ou un
hexagone complet (cinq sommets et toutes les arêtes possibles). Sur ces deux figures complémentaires:
Le nombre R(3, 5) est plus grand que 13. |
|
|
|
Borne supérieure On se réfère à l'inégalité
des nombres de Ramsey. Voir Table
des valeurs |
R(3, 5) ≤ R(2, 5) + R(3, 4) = 5 + 9 = 14 On a donc: 13<
R(3, 5) ≤ 14 => R(3, 5) = 14
|
||
|
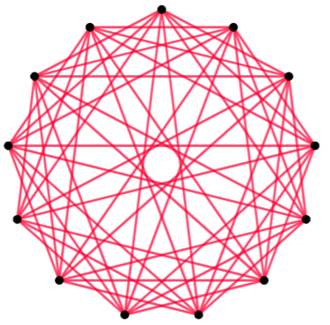
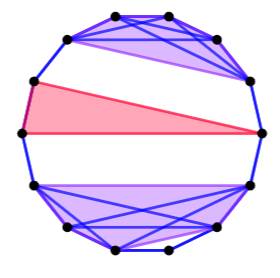
Exemple de tracé Avec 14 sommets, il est possible de créer
plusieurs pentagones complets. Il est même impossible de ne pas en créer un. Tracé inévitable Illustrer l'apparition inévitable d'un pentagone
complet n'est pas simple. |
Exemple de tracé de triangle et
pentagones complets
Quatre
quadrilatères complets. |
||
|
En terme de complémentaire Pour tout graphe d'au moins 14 sommets (R14),
soit G contient un triangle, soit son complémentaire Gc, contient
un hexagone complet (R5). |
En résumé, on dit que:
Rk
est le graphe complet à k sommets |
||
|
Deux à deux Dans une assemblée de 14 personnes,
|
Cas 3, 5 Dans une assemblée de 14 personnes, il est toujours
possible de trouver, au moins:
|
|
Haut de page (ou
double-clic)
![]()
|
Retour |
|
|
|
Suite |
|
|
|
Voir |
|
|
|
Cette page |
http://villemin.gerard.free.fr/aMaths/Topologi/aaaRamse/R53.htm |
|