|
Édition du: 04/06/2023 |
|
INDEX |
Nombres et théorème de RAMSEY |
|||
|
|
||||
Faites un double-clic pour un retour en haut de page
![]()
|
Connaissances et Ramsey Théorème des amis et des étrangers
Il est question
de réunions dans lesquelles les personnes se connaissent ou non. Il s'agit
d'une situation binaire comme on la retrouve dans la coloration des graphes
avec deux couleurs. Il n'est pas étonnant
qu'on y rencontre aussi les nombres de Ramsey. |
||
|
|
Sommaire de cette page >>> Approche >>> Assemblées et graphes >>> Historique >>> Exemples |
Débutants Glossaire |
|
Anniversaire et réunion de famille On connait le fait non intuitif que dans une
classe de 23 élèves, il y a une probabilité de 50 % de trouver deux personnes
ayant le même jour anniversaire. Avec ces anniversaires, il s'agit d'une PROBABILITÉ. Avec les réunions de famille et les nombres de Ramsey, il s'agit d'une CERTITUDE. |
Supposons que six
personnes soient réunies lors d'un dîner. Alors, il y a nécessairement un groupe de trois personnes à la fête qui sont soit toutes des
connaissances communes, soit toutes des étrangers communs. Résulte du fait que: R(3, 3)
= 6. |
|
|
Nombre de Ramsey R(m, n) Ces nombres sont solutions au problème de la
soirée qui cherche à connaitre le nombre minimum d'invités R(m, n) qui
doivent être invités pour qu'au moins m se connaissent ou au moins n ne se
connaissent pas l'un l'autre. |
Réunion à 9 Dans une assemblée de neuf personnes, il y aura
toujours, au moins, quatre personnes qui se connaissent mutuellement ou trois
qui ne se connaissent pas du tout; ou inversement. Résulte du fait que: R(3, 4)
= R(4, 3) = 9. |
|
|
Théorème de Ramsey Soit k ≥ 1. Si n est suffisamment grand,
alors dans tout groupe de n personnes, on peut en trouver k qui sont deux à
deux amies entre elles, ou bien k qui sont deux à deux non-amies entre elles. |
Réunion à 18 Dans une assemblée de 18 personnes, on est
certain de trouver:
Résulte du fait que: R(4, 4)
= 18. |
|
Voir Connaissances
/ Deux
couleurs pour graphe à six nœuds / Principe
des tiroirs
|
Réunion et graphe représentatif Pour avoir une meilleure idée de ce que cela
signifie, considérons un exemple classique, dans lequel les points (les sommets) représentent les
invités à une fête. Colorez le segment (arête) entre deux invités en
rouge s'ils se sont déjà rencontrés et en bleu s'ils ne l'ont pas fait. Graphe complet monochrome ou clique En invitant suffisamment de personnes à la fête,
vous ne pourrez pas éviter d'y trouver un groupe de personnes qui se
connaissent toutes entre elles (une clique) ou d'y rencontrer un
groupe de personnes qui ne se sont jamais rencontrés, ni l'une ni l'autre,
auparavant. Au moins une clique, c'est la
normalité En effet, la chose la plus commune en présence
d'un graphe est qu'il existe une clique monochromatique: une structure
colorée (graphe complet)
d'une seule couleur. |
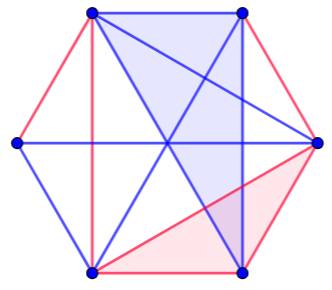
Exemple de deux cliques avec six sommets:
un triangle bleu et un triangle rouge
Avec six sommets, le
polygone complet compte toujours au moins un triangle monochromatique (de
même couleur ou de couleurs différentes). En fait, il s'avère qu'il y
en aura deux. |
|
|
C'est vers
les années 1950 que le problème de la réunion (Party Acquaintance) est apparu
dans la littérature mathématique. Il est publié dans la section des problèmes
de l'American Mathematical Monthly en 1958. Martin Gardner en a parlé à trois reprises dans
ses chroniques. Le défi était: prouvez que dans une fête de six
personnes, soit il y a trois connaissances communes, soit il y a trois
inconnus communs. Paul Erdös
a proposé sa méthode probabiliste pour prouver une généralisation. |
Ce défi est parfois connu sous le nom de théorème de l'amitié, théorème sur les amis et les
étrangers, ou théorème de Ramsey (Friendship Theorem, a Theorem on
Friends and Strangers, or Ramsey's Theorem) Le problème peut être modélisé par un graphe
bicolore. Pour rappel, Rn est la notation
standard pour un graphe complet à n sommets. Supposons que les bords de R6 soient
tous colorés en deux couleurs : rouge ou bleu. Le résultat est équivalent à
l'affirmation que pour toute coloration de ce type, il existe toujours un
triangle monochromatique (un R3). En fait, il a été montré par A. W. Goodman (1959)
que le nombre de triangles monochromatiques est d'au moins 2. |
|
Voir Historique de la
théorie de Ramsey
|
R(3, 3) = 6 |
Dans une assemblée de 6 personnes, on est certain
de trouver
|
|
|
R(4, 4) = 18 |
Dans une assemblée de 18 personnes, on est
certain de trouver
|
|
|
R(5, 5) = {43-48} |
Dans une assemblée de k personnes, on est certain
de trouver
On ne connait pas la valeur de k qui est comprise
entre 43 et 48. |
|
|
R(3, 4) = 9 |
Dans une assemblée de 9 personnes, on est certain
de trouver
Ou l'inverse. |
|
|
R(3, 5) = 14 |
Dans une assemblée de 14 personnes, on est
certain de trouver
Ou l'inverse. |
|
|
R(4, 5) = 25 |
Dans une assemblée de 25 personnes, on est
certain de trouver
Ou l'inverse. Résultat connu publié en 1995. |
|
|
R(3, 3, 3) = 17 |
Chacun de ces 17 étudiants parlent avec chacun
des autres. Chaque couple d'étudiants discute d'un des trois sujets. Alors, inévitablement, trois étudiants parlent du
même sujet entre eux. |
|
Haut de page (ou
double-clic)
![]()
|
Retour |
|
|
|
Suite |
|
|
|
Voir |
|
|
|
Cette page |
http://villemin.gerard.free.fr/aMaths/Topologi/aaaRamse/Assemble.htm
|
|