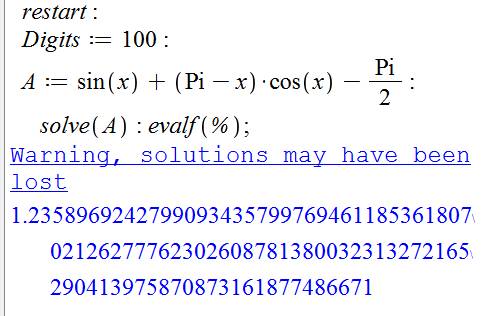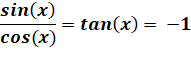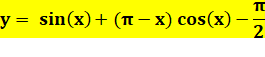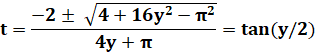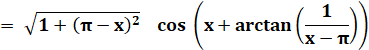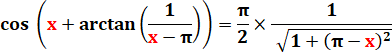NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 01/03/2024 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Trigonométrie
Débutants Trigonométrie	CALCULS AVANCÉS				Glossaire FORMULES
INDEX Trigonométrie Calculs	Introduction	Exercices 01	Exercices 02	Exercices 03
	Calculs simples	Angles triangle	Exercice 04
	Bissectrice (1 ± cosa + i.sina)		Citerne au quart remplie
		Sommaire de cette page >>> Résolution par dichotomie >>> Résolution avec logiciel de calcul Exploration >>> Approche – Formule simple >>> Ajout d'un terme constant >>> Ajout d'un coefficient >>> L'équation demandée – Allure du graphe >>> L'équation demandée – Résolution >>> Méthode additive >>> Bilan

Calculs en trigonométrie – 03

Résoudre

Cette équation est rencontrée dans le problème de la chèvre qui broute dans un champ circulaire.

C'est une équation trigonométrique qui multiplie les difficultés. Elle présente à la fois un terme constant (Pi/2) et un coefficient (Pi –x) qui contient l'inconnu en clair et non sous la forme d'une ligne trigonométrique.

C'est une équation transcendantale. Ce qui veut dire qu'elle ne peut pas être résolue algébriquement, qu'elle n'a pas de solution analytique. Seule une résolution graphique ou par calculs itératifs permet d'approcher la solution par approximations successives.

Après avoir montré comment trouver la solution, nous allons apprivoiser cette équation en observant son graphe. Nous tenterons de la formuler d'une autre manière, sachant que la tentative est vaine, mais cet exercice permettra de manipuler quelques propriétés des lignes trigonométriques.

Formule texte: sin(x)+(pi-x)*cos(x)=pi/2

Résolution par dichotomie sur tableur
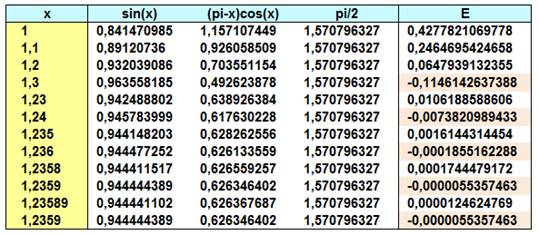
La formule est implantée sur tableur. Ici, on a montré le calcul terme par terme. Le résultat (E) doit être nul. Pour chaque nouvelle décimale de la solution, on cherche les deux chiffres qui encadrent la solution; l'une donnant une valeur positive, l'autre négative. Avec ce tableau, on trouve une solution à cinq décimales: x = 1,23589…	Tableau de calcul avec objectif: écart E = 0 Formules utilisées

Résolution avec logiciel de calcul
Solution avec un logiciel de calcul comme Maple. Ici, nous avons demandé un calcul avec 100 chiffres. L'instruction "solve" (résoudre en anglais) conduit a des réponses multiples et le logiciel nous prévient qu'il a peut être perdu des solutions en route. Néanmoins, avec evalf (évaluation en flottant), la valeur principale avec 100 chiffres nous est donnée.

Voir Programmation – Index

Bilan

Les équations transcendantales se résolvent par méthodes graphique ou par méthodes itératives: dichotomie ou méthode de Newton en utilisant une calculette ou un tableur.

Exploration – Allure du graphe et tentatives de calculs trigonométrique

Approche sans terme constant
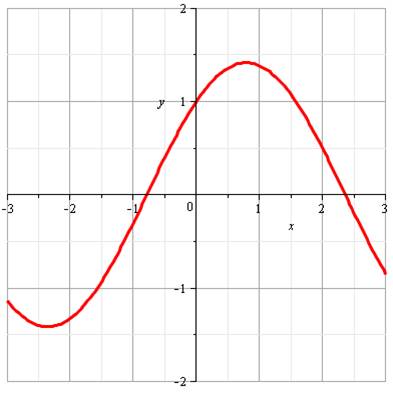
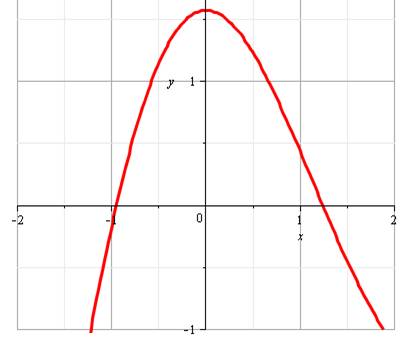
Allure du graphe de
Résolution de x = -1/4 + k i = - 0,7853981635 + k Effectivement, pour x = 45°, sinus et cosinus son égaux à . Notons: x = 0; y = 1

Avec un terme constant
La courbe est translatée de Pi/2 vers le bas et elle ne coupe plus l'axe des x, l'équation n'a pas de solution. On a bien pour x = 0, y = 1 – Pi /2 = -0,57079…

Avec un coefficient
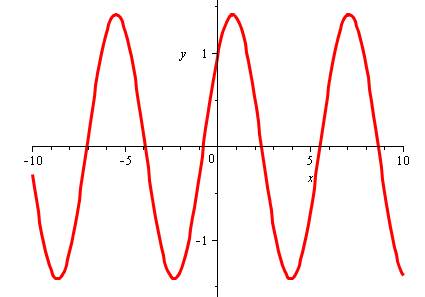
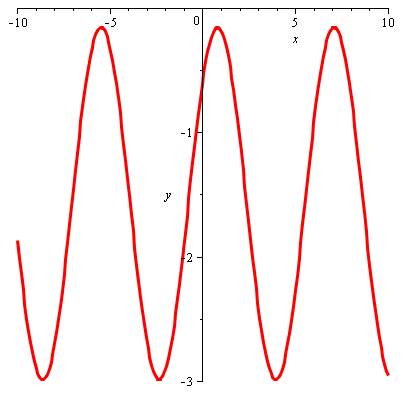
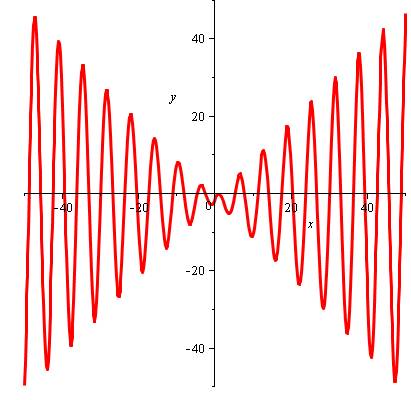
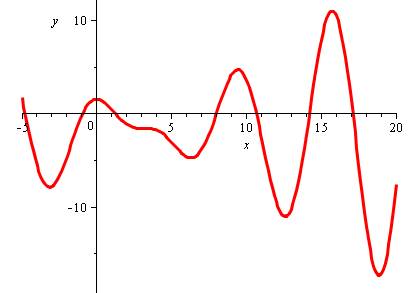
Le graphe montre une courbe oscillante, amortie au passage au zéro. La modulation est due au coefficient en x qui éteint le cosinus au voisinage du zéro.
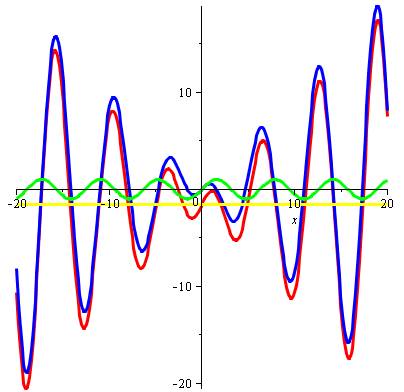
Contribution de chaque terme: · Bleu: graphe complet · Rouge: x cos(x) · Vert: sinus(x) · Jaune: - Pi / 2
Zoom au voisinage de 0. x = 5,203247732 x = -2,553845 x = 0; y = Pi/2

L'équation demandée
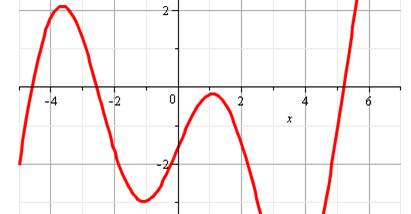
Le graphe montre une courbe oscillante, amortie au passage au zéro du même style que la précédente
Zoom autour de zéro
Deux solutions autour de zéro: x = – 0,9487368040 x = 1,235896924 x = 0 ; y = Pi /2

Résolution par la méthode des tangentes
Changement de variable x = 2y + Pi pour éliminer le Pi devant cos(x) et avec 2y pour pouvoir utiliser les formules en tangentes. Utilisation d'un calculateur pour résoudre les équations.
Équation demandée
x = 2y + pi
Avec les tangentes t = tan(y/2)
1 + t² >0
Résolution en t
Résolution en y	y1 = -2,045164729 y2= - 0,9528478647 y3 = - 3,963193805 y4 = 5,523693468
x = y + pi	x1 = - 0,948736804 x2 = 1,235896925 x3 = - 4,784794956 x4 = 14,18897959

Résolution par la méthode additive
Cette méthode consiste à transformer une somme sinus plus cosinus en un simple cosinus. Elle est très pratique, mais, ici l'angle dans le coefficient reste gênant.
Équation demandée:
Banalisation des coefficients et égalisation à un cosinus.
Or le cosinus se développe en:
En identifiant les parties identiques:
Soit la valeur de a en divisant, puis en revenant à notre exemple.
En ajoutant les carrés de a et b.
Somme sin + cos devient:
Et l'équation de départ:
Une des solutions (pas facile à trouver sans ordinateur).	x = 1,235896925…
Vérification	a = 1,9… b = 1 r = 2,15 … k = -0,48… r (cos(x + k) = 1,570 … = Pi /2 (Pi – x) cos (x) = 0,626 … sin(x) = 0,944 … Somme = 1,570 … = Pi /2

Bilan

Vous noterez en comparant au graphe que nous n'avons pas toutes les solutions; elles sont en nombre infini.

Les deux méthodes utilisées débouchent chacune sur la résolution d'une nouvelle équation problématique.

Si l'on souhaite résoudre cette équation avec un logiciel, alors, inutile de faire tous ces calculs. Maple résout aussi bien l'équation de départ, comme vu en entrée de cette page.

Retour	· Calculs simples – Pente · Exercices de trigonométrie 02
Suite	· Problème de la chèvre dans un champ circulaire · Citerne au quart remplie
Voir	· Trigonométrie – Débutant · Trigonométrie – Calculs simples · Trigonométrie – Formules
Aussi	· Angle et cercle trigonométrique
Cette page	http://villemin.gerard.free.fr/aMaths/Trigonom/CalcAv03.htm