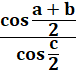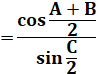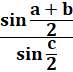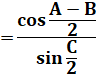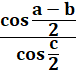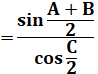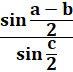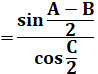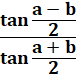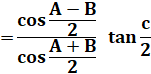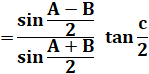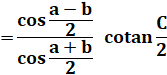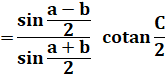NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 16/01/2022 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Trigonométrie
Débutants Trigonométrie	IDENTITÉS – FORMULES					Glossaire Général
INDEX Outils de trigo Trigonométrie Analyse Identités	Identités générales		Angles multiples		Addition d'angles
	Linéarisation		Euler–Moivre		Formules avancées
			Angles A, B et C		Sphérique
	Démonstrations des identités			Calculs particuliers
		Sommaire de cette page >>> Formules de Gauss >>> Formules de Neper

RELATIONS en TRIGONOMÉTRIQUE

sphérique

Formule de Gauss et de Neper

Notion avancée: formules trigonométriques en (a + b) / 2

impliquant les distances sphériques.

Voir Table des valeurs trigonométriques / Les angles particuliers un par un

Angles: A, B et C

Distances sphériques d'un triangle sphérique: a, b et c

Formules des cosinus et des sinus

Formules de Gauss

Formules de Neper

Bases	Trigonométrie – Débutant Trigonométrie – Tables Relations dans le triangle quelconque Relations dans le triangle rectangle
Voir	Angles et informations concernant un angle particulier Faire le tour du cercle (relations de base) Sinus et aire du triangle isocèle Calculs en trigonométrie (simples) Calculs en trigonométrie (avancés) Formulaires – Index Linéarisation: puissances des fonctions trigonométriques Relations trigonométriques dans le triangle quelconque
Aussi	Triangle Pentagone Identités remarquables
Sites	Trigonométrie sphérique – Wikipédia La trigonométrie sphérique, simplifiée dans ses formules et démonstrations – Cornélius Keogh et V.-A. Lebesgue
Cette page	http://villemin.gerard.free.fr/aMaths/Trigonom/aaaBases/Reldemi.htm