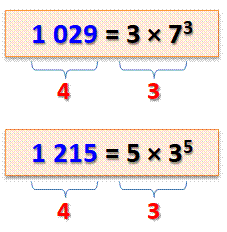|
Édition du: 18/09/2021 |
|
INDEX |
Types de Nombres – Motifs |
|||
![]()
|
NOMBRES FRUGAUX ou ÉCONOMES |
||
|
|
Sommaire de cette page >>> Approche et définition >>> Nombres modestes – Listes >>> Nombres modestes au sens étendu – Records |
Débutants Glossaire |
Anglais: frugal numbers or
economical numbers
|
Prenons le nombre 512 = 29
Moins de chiffres pour écrire la factorisation que pour l'écrire
lui-même: le nombre est frugal ou économe. |
|
|
|
Définition Un nombre n est frugal si la quantité de chiffres de sa
factorisation, y compris les exposants (hors 1) est inférieure à la quantité
de ses propres chiffres. Avec la même quantité, le nombre n est équidigital. Avec plus, il est prodigue. |
#Chiffres(N) > #Chiffres(factorisation) |
|
|
Nombres frugaux jusqu'à 20 000 125, 128, 243, 256,
343,
512,
625,
729, 1024,
1029, 1215, 1250, 1280, 1331, 1369, 1458, 1536, 1681, 1701, 1715, 1792, 1849,
1875, 2048, 2187, 2197, 2209, 2401, 2560, 2809, 3125, 3481, 3584, 3645, 3721,
4096, 4374, 4375, 4489, 4802, 4913, 5041, 5103, 5329, 6241, 6250, 6561, 6859,
6889, 7203, 7921, 8192, 9375, 9409, 10000, 10082, 10112, 10125, 10201, 10206,
10240, 10368, 10375, 10443, 10449, 10496, 10609, 10624, 10625, 10633, 10658,
10752, 10935, 10976, 10985, 11008, 11045, 11125, 11163, 11392, 11421, 11449,
11664, 11767, 11776, 11875, 11881, 11907, 12005, 12032, 12125, 12167, 12288,
12393, 12416, 12482, 12500, 12544, 12691, 12769, 12800, 12879, 12943, 13122,
13125, 13467, 13568, 13718, 13778, 13824, 13851, 14045, 14063, 14336, 14337,
14375, 14406, 14641, 14739, 14749, 14823, 14848, 15104, 15123, 15309, 15379,
15463, 15552, 15616, 15625, 15842, 15872, 15987, 16000, 16121, 16129, 16281,
16384, 16767, 16807, 16875, 17152, 17161, 17253, 17405, 17496, 17739, 17920,
18125, 18176, 18179, 18225, 18605, 18688, 18723, 18750, 18769, 18818, 18944,
19197, 19208, 19321, 19375, 19663, 19683, 20000. Nombres frugaux jusqu'à 2048 avec
leur factorisation [125, 5^3],
[128, 2^7], [243, 3^5], [256, 2^8], [343, 7^3], [512, 2^9], [625, 5^4], [729, 3^6], [1024, 2^10], [1029, 3×7^3], [1215, 5×3^5], [1250, 2×5^4], [1280, 5×2^8], [1331, 11^3], [1369, 37^2], [1458, 2×3^6], [1536, 3×2^9], [1681, 41^2], [1701, 7×3^5], [1715, 5×7^3], [1792, 7×2^8], [1849, 43^2], [1875, 3×5^4], [2048, 2^11]. |
|
|
Nombres
équidigitaux jusqu'à 1000 (ils sont 273) 1, 2, 3, 5, 7, 10, 11, 13, 14, 15, 16, 17, 19,
21, 23, 25, 27, 29, 31, 32, 35, 37, 41, 43, 47, 49, 53, 59, 61, 64, 67, 71, 73,
79, 81, 83, 89, 97, 101, 103, 105, 106, 107, 109, 111, 112, 113, 115, 118,
119, 121, 122, 123, 127, 129, 131, 133, 134, 135, 137, 139, 141, 142, 145,
146, 147, 149, 151, 155, 157, 158, 159, 160, 161, 162, 163, 166, 167, 169,
173, 175, 177, 178, 179, 181, 183, 185, 189, 191, 192, 193, 194, 197, 199,
201, 203, 205, 211, 213, 215, 217, 219, 223, 224, 227, 229, 233, 235, 237,
239, 241, 245, 249, 250, 251, 257, 259, 263, 265, 267, 269, 271, 277, 281,
283, 287, 289, 291, 293, 295, 301, 305, 307, 311, 313, 317, 320, 329, 331,
335, 337, 347, 349, 353, 355, 359, 361, 365, 367, 371, 373, 375, 379, 383,
384, 389, 395, 397, 401, 405, 409, 413, 415, 419, 421, 427, 431, 433, 439,
443, 445, 448, 449, 457, 461, 463, 467, 469, 479, 485, 486, 487, 491, 497,
499, 503, 509, 511, 521, 523, 529, 541, 547, 553, 557, 563, 567, 569, 571,
577, 581, 587, 593, 599, 601, 607, 613, 617, 619, 623, 631, 640, 641, 643,
647, 653, 659, 661, 673, 677, 679, 683, 686, 691, 701, 709, 719, 727, 733,
739, 743, 751, 757, 761, 768, 769, 773, 787, 797, 809, 811, 821, 823, 827,
829, 839, 841, 853, 857, 859, 863, 875, 877, 881, 883, 887, 896, 907, 911,
919, 929, 937, 941, 947, 953, 961, 967, 971, 977, 983, 991, 997, 1000. Dont nombres équidigitaux composés
(ils sont 105), car tous les premiers sont équidigitaux 1, 10, 14, 15, 16, 21, 25, 27, 32, 35, 49, 64,
81, 105, 106, 111, 112, 115, 118, 119, 121, 122, 123, 129, 133, 134, 135,
141, 142, 145, 146, 147, 155, 158, 159, 160, 161, 162, 166, 169, 175, 177,
178, 183, 185, 189, 192, 194, 201, 203, 205, 213, 215, 217, 219, 224, 235,
237, 245, 249, 250, 259, 265, 267, 287, 289, 291, 295, 301, 305, 320, 329,
335, 355, 361, 365, 371, 375, 384, 395, 405, 413, 415, 427, 445, 448, 469,
485, 486, 497, 511,
529,
553, 567, 581, 623, 640, 679, 686, 768, 841, 875, 896, 961, 1000 Leurs facteurs [1, 1], [10, 2×5], [14, 2×7], [15, 3×5], [16,
2^4], [21, 3×7], [25, 5^2], [27, 3^3], [32, 2^5], [35, 5×7], [49, 7^2], [64,
2^6], [81, 3^4], [105, 7×(3×5)], [106, 2×53], [111, 3×37], [112, 7×2^4],
[115, 5×23], [118, 2×59], [119, 7×17], [121, 11^2], [122, 2×61], [123, 3×41],
[129, 3×43], [133, 7×19], [134, 2×67], [135, 5×3^3], [141, 3×47], [142,
2×71], [145, 5×29], [146, 2×73], [147, 3×7^2], [155, 5×31], [158, 2×79],
[159, 3×53], [160, 5×2^5], [161, 7×23], [162, 2×3^4], [166, 2×83], [169,
13^2], [175, 7×5^2], [177, 3×59], [178, 2×89], [183, 3×61], [185, 5×37],
[189, 7×3^3], [192, 3×2^6], [194, 2×97], [201, 3×67], [203, 7×29], [205,
5×41], [213, 3×71], [215, 5×43], [217, 7×31], [219, 3×73], [224, 7×2^5],
[235, 5×47], [237, 3×79], [245, 5×7^2], [249, 3×83], [250, 2×5^3], [259,
7×37], [265, 5×53], [267, 3×89], [287, 7×41], [289, 17^2], [291, 3×97], [295,
5×59], [301, 7×43], [305, 5×61], [320, 5×2^6], [329, 7×47], [335, 5×67],
[355, 5×71], [361, 19^2], [365, 5×73], [371, 7×53], [375, 3×5^3], [384,
3×2^7], [395, 5×79], [405, 5×3^4], [413, 7×59], [415, 5×83], [427, 7×61],
[445, 5×89], [448, 7×2^6], [469, 7×67], [485, 5×97], [486, 2×3^5], [497,
7×71], [511, 7×73], [529, 23^2], [553, 7×79], [567, 7×3^4], [581, 7×83],
[623, 7×89], [640, 5×2^7], [679, 7×97], [686, 2×7^3], [768, 3×2^8], [841,
29^2], [875, 7×5^3], [896, 7×2^7], [961, 31^2], [1000, 2^3×5^3] |
|
![]()
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |