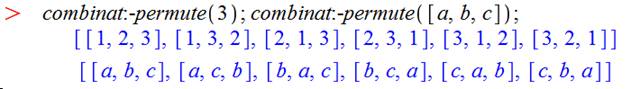|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
PERMUTATIONS Algorithmes et leurs performances Il existe plusieurs méthodes pour produire
toutes les permutations d'un ensemble d'objets. On rappelle qu'une liste de n éléments engendre n! (factorielle
n) cas de permutations. Par exemple, 3 628 800 cas pour n = 10. Même avec les
moyens actuels, il est impossible de dresser toutes les permutations au-delà
de n = 15. Si le calcul pour n = 10 dure une seconde pour n = 15, il faudrait
100 heures soit un peu plus de 4 jours et, surtout, une grande quantité de
pages pour les écrire. Avec l'arrivée des ordinateurs, les
mathématiciens et les informaticiens ont étudié les meilleurs algorithmes pour minimiser le
temps d'exécution. Les plus rapides sont ceux qui occasionnent un seul
mouvement de permutation par itération. C'est le cas pour l'algorithme de
Heap et l'algorithme de Steinhaus-Jonhson-Trotter. Le premier (Heap) est sans
doute plus simple à implémenter. Compte tenu de l'usage des permutations, la
vitesse de calcul n'est pas d'une grande importance. La recherche
d'améliorations est cependant un excellent moyen de faire progresser la
science de l'algorithmique. |
|
La
majorité des logiciels mathématiques incorpore la fonction permutation.
Exemple avec Maple:
|
|
Les
algorithmes les plus simples produisent les permutations classiques par ordre
lexicographique (alphabétique et nombres croissants). Le logiciel de
permutation Maple utilise ce procédé. Exemple: n = 4 avec chiffres [1,
2, 3, 4], [1, 2, 4, 3], [1, 3, 2, 4], [1, 3, 4, 2], [1, 4, 2, 3], [1, 4, 3,
2], [2, 1, 3, 4], [2, 1, 4, 3], [2, 3, 1, 4], [2, 3, 4, 1], [2, 4, 1, 3], [2,
4, 3, 1], [3, 1, 2, 4], [3, 1, 4, 2], [3, 2, 1, 4], [3, 2, 4, 1], [3, 4, 1,
2], [3, 4, 2, 1], [4, 1, 2, 3], [4, 1, 3, 2], [4, 2, 1, 3], [4, 2, 3, 1], [4,
3, 1, 2], [4, 3, 2, 1] Exemple: n = 3 avec mots [Riri,
Fifi, Loulou], [Riri, Loulou, Fifi], [Fifi, Riri, Loulou], [Fifi, Loulou,
Riri], [Loulou, Riri, Fifi], [Loulou, Fifi, Riri] |
Suite et programmation expliquée en détail en Récursivité
Voir Permutations des lettres
dans un mot (calcul des permutations et arrangements)
![]()
Méthodes plus
sophistiquées et plus rapides
|
|
||
|
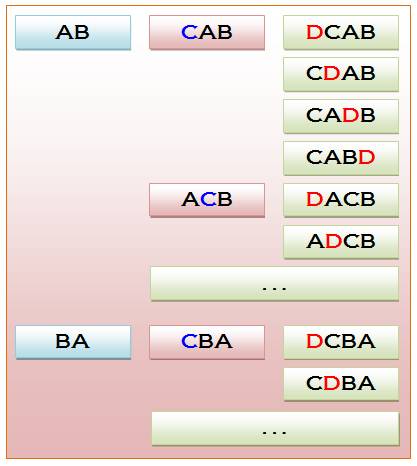
Une première idée de production des
permutations Les deux
premiers éléments (noirs) sont permutés. L'élément
suivant (bleu puis rouge) est inséré entre chaque espace entre les éléments
déjà placés. Définition récursive: 1)
trouvez toutes des permutations avec n – 1 éléments; et 2)
insérez les éléments restants dans tous les espaces possibles des éléments de
la permutation n – 1. |
|
|
|
|
|||
|
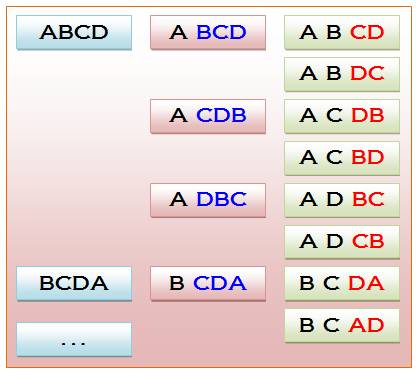
Principe
de l'algorithme de Heap On fixe
le premier élément A et on permute le reste
(BCD). Pour
permuter le reste, on fixe le premier élément (B) et on permute le reste
(CD). Etc. Méthode, comme on le voit récursive (méthode qui fait appel à
elle-même) Méthode à modification minimale, puisque chaque permutation est obtenu
à partir de la précédente avec une simple permutation de deux éléments. |
|
||
|
En
pratique L'algorithme
de Heap est souvent présenté dans l'autre sens (plus pratique pour sa
programmation). Les
éléments fixes sont à droite et on permute ce qui reste à gauche. |
123 213 312 132 231 321 |
Départ. Le
3 est fixe, permutation des deux premiers. Permutation
des deux extrémités. Le
2 est fixe, permutation des deux premiers. Permutation
des deux extrémités. Le
1 est fixee, permutation des deux premiers. |
|
|
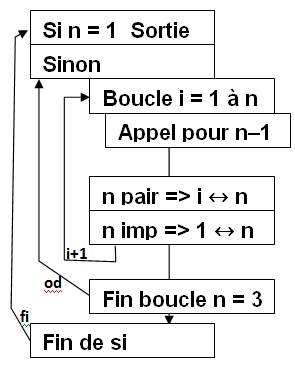
Permutation d'une chaîne comptant n éléments L'algorithme (procédure) engendre les (n – 1)! permutations des n – 1
premiers éléments. Le dernier élément étant fixé. La procédure fait appel à elle-même, en cascade pour n de plus en plus
petit (procédure récursive). Si n = 1, la récursivité de ce
niveau est atteinte et le programme délivre une des permutations. Sinon, la procédure s'appelle elle-même pour le n immédiatement
inférieur (n – 1). Après travail aux niveaux inférieurs, le programme est de retour à ce
niveau de récursivité, le programme opère la permutation magique de Heap
|
|
|
Programmation
de l'algorithme de Heap Méthode
récursive |
Vous reconnaissez exactement l'algorithme indiqué. Son implémentation
sous Maple est assez simple;
de même que sous bien d'autres logiciels. Le secret du fonctionnement tient
dans la distinction en local et global. Faute de le faire, vous allez vous
arracher les cheveux à la mise au point! La chaine à permuter (ici AA) doit être déclarée en GLOBAL (et non en
local). Sinon Le programme en remontant une étape de récursion, oublie la
permutation qu'il a effectuée. Il reprend la permutation qu'il a mémorisée en
local, c'est-à dire au niveau k de la récursivité et non aux niveaux plus
profonds où il a travaillé. Note: ce programme retourne la liste des permutations
avec lprint en 5e ligne. Je n'ai pas trouvé l'astuce qui
permettrait de retourner une liste avec return. Si quelqu'un
sait je suis preneur! |
|
|
En rouge, programme demandant la permutation de 5 éléments. N est la quantité d'éléments obtenue par nops(A). On aurait tout aussi
bien pu l'écrire directement. En bleu, le début de la liste des 120 permutations. Note aux programmeurs: vous trouverez
ce même code sur divers sites Internet. Aucun ne marche
correctement sans adaptation au langage utilisé. Pour une raison qui m'est inconnue, Wikipedia (anglais) ajoute un
extra appel à la procédure. |
Voir Programmation – Index
|
|
|||
|
Algorithme classique
de permutations |
Algorithme SJT de permutations |
||
|
Les algorithmes
classiques délivrent les permutations à partir d'un ordre lexicographique
(alphabétique ou croissants pour les nombres). Ces algorithmes
fonctionnent par propagation. |
Cet
algorithme (comme Heap) délivre une
permutation à chaque opération et dans un ordre particulier. Cet algorithme
fonctionne par cheminement direct parmi toutes les permutations. |
||
|
1 2 3 1 3 2 2 1 3 2 3 1 3 1 2 3 2 1 |
1 2 3 1 3 2 3 1 2 3 2 1 2 3 1 2 1 3 |
Découvert indépendamment par Johnson et Trotter vers 1960 et même
avant sous une certaine forme par Steinhaus. >>> |
|
|
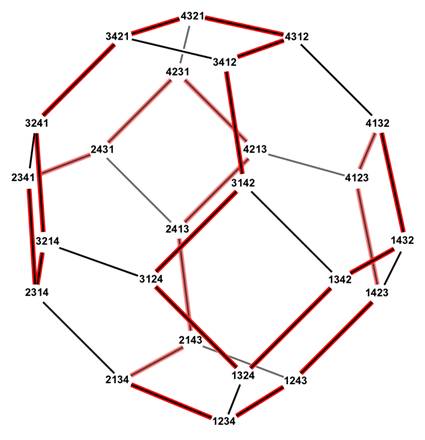
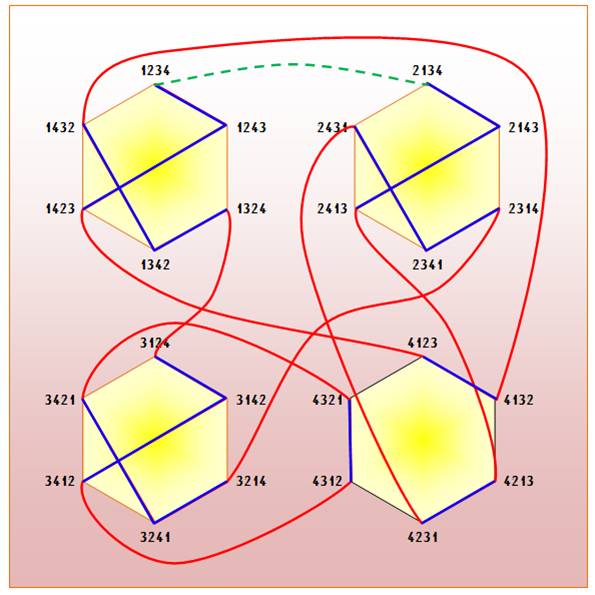
Principe
de l'algorithme SJT Le graphe de
toutes les permutations forme un polyèdre.
L'astuce consiste à parcourir un chemin
hamiltonien entre les sommets (chemin qui passe une fois et une seule par
tous les sommets). |
Cela rappelle le code
binaire Gray qui change un seul bit pour passer d'un nombre binaire à un
autre. |
|
On commence par
écrire tous les éléments dans l'ordre croissants |
1 2 3 (exemple) |
|
On donne une direction identique à chaque élément au départ |
|
|
Un nombre est mobile si le nombre pointé est plus petit. Les nombres aux
extrémités et pointant vers l'extérieur ne sont pas mobiles. |
Ci-dessus les
nombres 2 et 3 sont mobiles |
|
1) Prendre
l'élément mobile le plus grand et permuter avec le voisin pointé. |
|
|
2) Vérifier s'il
existe des plus grands mobiles. Si oui, changer leur direction |
ici, non |
|
3) Sinon,
poursuivre avec le plus grand en cours de traitement (3). |
|
|
Cet élément est
en bout de course, alors, reprendre l'étape 1. |
|
|
Y'a-t-il un plus
grand que le 2, oui le 3, alors on inverse le sens. |
|
|
Ce nombre 3
redevient le plus grand mobile. |
|
|
Nouvelle
possibilité de permutation. |
|
|
Aucun n'est
mobile. |
Fin |
Algorithme STJ générique
|
Mettre
les éléments dans l'ordre croissant. Tant
qu'il existe un élément mobile:
|
|
STJ avec
quatre nombres Les 24 étapes de
permutation avec configuration et explications. Le sens associé à
chaque nombre est symbolisé par un point. |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Permutohedron Nom donné par Guilbaud
& Rosenstiehl en 1963. Schoute fut le premier
à étudier ces polyèdres en 1911. |
Source image: Wikipédia |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Cheminement
à travers le graphe des permutations classiques (simple exercice)
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Une belle histoire du XVIIe siècle en Angleterre
|
Un
groupe de personnes forme un cercle. Chacun doit faire sonner une grosse
cloche à l'aide d'une corde. Pour éviter la monotonie de la mélodie, la
séquence doit être régulièrement changée. Or, chaque cloche tinte durant un
bon moment et ne peut pas être relancée trop rapidement. Par exemple, la
cloche actuellement en 3e position ne pourra jouer qu'en 2e
ou en 4e. Le passage d'une
permutation à la suivante avec une seule permutation était donc déjà connue à
cette époque. |
|
|
||
|
Définitions Complexité
en O (n! . n). Si une opération
dure t secondes, il faudra faire n! manipulations pour le n! permutations fois
n manipulations pour les n éléments de la chaine à permuter. La durée
d'exécution sera : n! . n . t secondes. C'est celle
valeur qui est souvent donnée pour l'exécution des algorithmes classiques Complexité
en O (n!). Impossible de
réduire la quantité d'opération à moins que la quantité de permutations (n!). C'est cette
valeur qui est donné pour l'exécution de l'algorithme SJT. |
Étude de
Youssef Bassil (2012) Alors que les
algorithmes se valent jusqu'à une longueur de n =6 éléments à permuter, l'algorithme
SJT supplante nettement les valeurs de n supérieures. C'est le cas également
avec l'algorithme de Heap L'auteur donne
pour une longueur 10:
Un rapport égal à
5 qui croit encore avec la longueur à permuter. Voir
Référence |
|
|
Nouveautés Ces algorithmes
sont régulièrement améliorés et d'autres voient le jour comme:
|
Malgré une certaine complexité
du codage, il est vrai que l'algorithme SJT et l'algorithme de Heap sont les
seuls à produire une configuration à partir de la précédente avec une seule
permutation de deux éléments adjacents. Les permutations
obtenues sont également sans symétrie: une moitié ne
contient aucune réflexion d'une configuration appartenant à l'autre moitié. |
|
|
|
|
|
Keywords: Permutation, algorithms, brute force, divide and conquer. Permutation is the different arrangements that can be made with a given number
of things taking some or all of them at a time. The notation P(n,r) is used
to denote the number of permutations of n things taken r at a time.
Permutation is used in various fields such as mathematics, group theory,
statistics, and computing, to solve several combinatorial
problems such as the job assignment problem and the traveling salesman problem.
Bottom-Up,
Lexicography, and Johnson-Trotter are three of the most popular permutation algorithms that emerged
during the past decades. Generally speaking, the Johnson-Trotter
algorithm checks to see whether a mobile number exists or not, if yes
the algorithm performs the following:
|
|
![]()
|
Suite |
|
|
Voir |
|
|
|
|
|
Cette page |
![]()