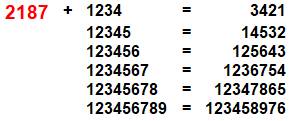|
|||||||||||||||||||||||||||||||||||||||||
PN:
Pannumériques
![]()
|
NOMBRES SEMI-PANNUMÉRIQUES ou SEMI-PANDIGITAUX Nombre formé avec les chiffres un, deux,
trois quatre et cinq. Leurs permutations et leur factorisation. Divisibilité par 3 et par 9 des
pannumériques partiels. |
Propriété remarquable du nombre
2 187
|
|
Martin Gardner |
|
|
|
|
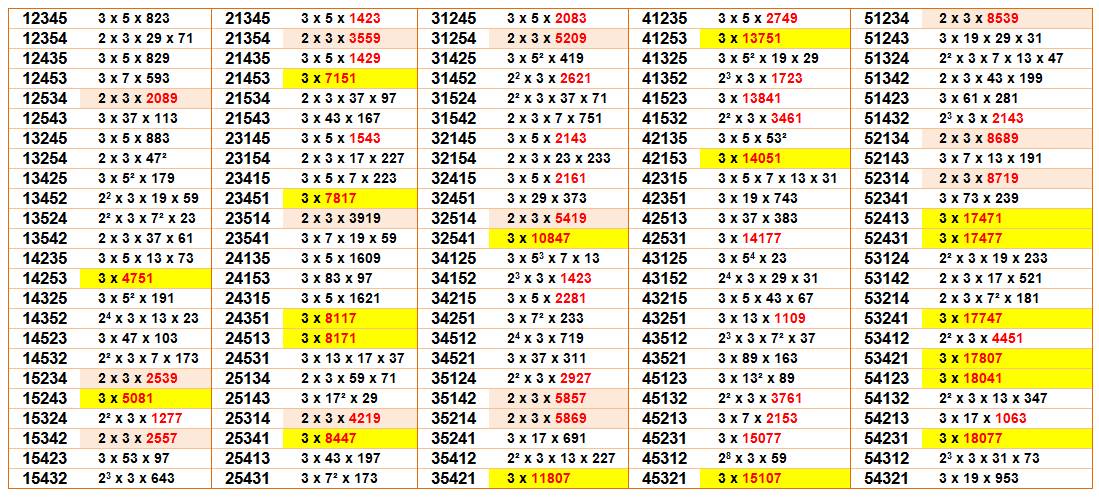
Exemples
de lecture Le nombre 12543 est divisible par 6 (couleur ocre) et
l'un des facteur est supérieur à 1000 (en rouge) Le nombre 14253 ne possède que deux facteurs
(jaune): 3 et un nombre supérieur à
1000
|
|
|
|
|
|
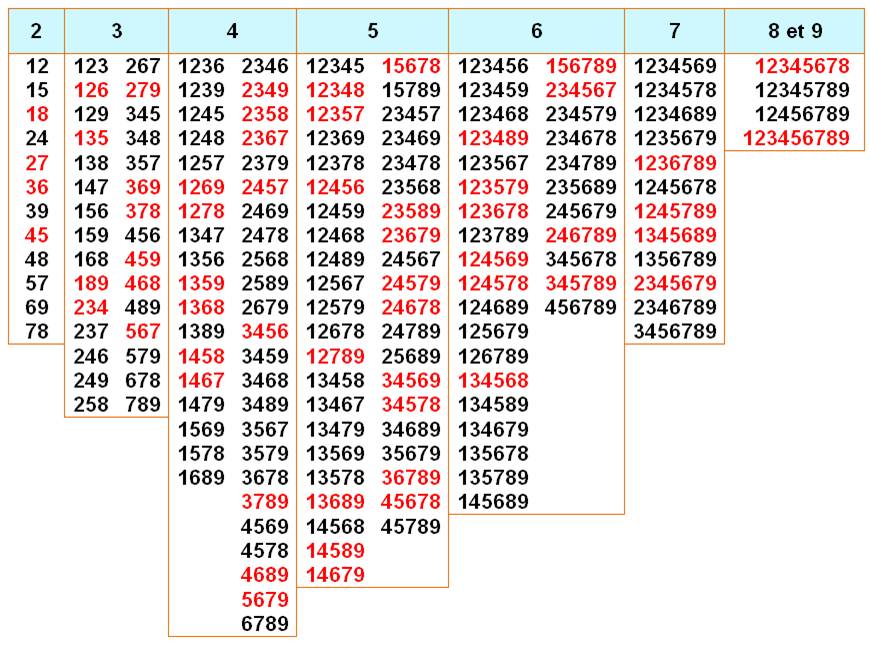
Exemples
de lecture Le nombre 18 et sa permutation 81 est divisible par 9
(rouge). Le nombre 123 et ses permutations (123, 132, 213, 231,
312, 321) sont divisibles par 3. Le nombre 267 et ses permutations (267, 276, 627, 672,
726, 762) sont divisibles par 3. |
|
|
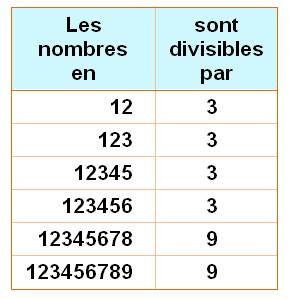
Toutes
les permutations du nombre pannumérique 123456789 sont divisibles par 9. Toutes
les permutations des nombres semi-pannumériques 12345 et 45789 (par exemple)
sont divisibles par 3. Mais le 56789 n'est pas divisible par 3. En
prenant les pannumériques partiels de plus en plus grands:
|
Voir Divisibilité par 9 des pannumériques
|
|
||
|
xxxxxyyyyyzzzzz |
5 fois trois chiffres identiques. |
|
|
Quantité de permutations de ce nombre. |
756 756 = Q = 15! / (5! x 5! x 5!) |
|
|
Conditions pour éliminer les
pairs tous en conservant les nombres à petits facteurs.
|
||
|
111112222233333 777778888899999 |
504 504 =
2Q / 3 |
|
|
222223333344444 444445555566666 666667777788888 |
252 252 =
Q / 3 |
|
|
333334444455555 555556666677777 |
504 504 =
2Q / 3 |
|
![]()
|
Suite |
|
|
Aussi |
|
|
Cette
page |
![]()