|
|||||||||||||||||||||||||||||||||||
![]()
|
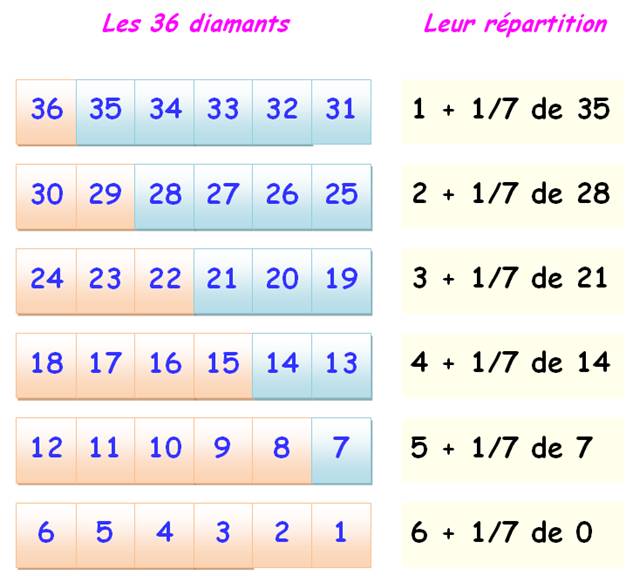
Énigme des diamants Qui débouche sur une propriété générale des carrés. |
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
Énigme
Solution
Exemple de
calcul: comment obtenir 28?
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
36 = (1 + 5) + (2 + 4) + (3 + 3) + (4 + 2) + (5 + 1) + (6 + 0)
= (1 + 35/7) + (2 + 28/7) + (3 + 21/7) + (4 + 14/7) + (5 + 7/7) + (6 +
0/7) |
|
|
|
|
|
Un carré est la
somme de deux nombres
triangulaires consécutifs.
Exemple avec 25 = 5² Le premier reçoit:
1 diamant + 1/6 de 25 – 1 = 1/6 de 24 = 4 Total 5 diamants;
reste 25 – 5 = 20 Le deuxième: 2
diamants + 1/6 de 20 – 2 = 1/6 de 18 = 3 Total 5 diamants;
reste 20 – 5 = 15 Le troisième: 3 diamants
+ 1/6 de 15 – 3 = 1/6 de 12 = 2 Total 5 diamants;
reste 15 – 5 = 10 Le quatrième: 4
diamants + 1/6 de 10 – 4 = 1/6 de 6 = 1 Total 5 diamants;
reste 10 – 5 = 5 Le cinquième: 5
diamants + 1/6 de 5 – 5 = 1/6 de 0 = 0 Total 5 diamants;
reste 5 – 5 = 0. Exemple avec C = c² de
3 à 10, avec F part fixe, V
part variable et R le reste à chaque fois F V R F V R F V R F V R 1 2 6 1 3 12 1 4 20 1 5 30 2 1 3 2 2 8 2 3 15 2 4 24 3 0 0 3 1 4 3 2 10 3 3 18 4 0 0 4 1 5 4 2 12 5 0 0 5 1 6 6 0 0 F V R F V R F V R F V R 1 6 42 1 7 56 1 8 72 1 9 90 2 5 35 2 6 48 2 7 63 2 8 80 3 4 28 3 5 40 3 6 54 3 7 70 4 3 21 4 4 32 4 5 45 4 6 60 5 2 14 5 3 24 5 4 36 5 5 50 6 1 7 6 2 16 6 3 27 6 4 40 7 0 0 7 1 8 7 2 18 7 3 30 8 0 0 8 1 9 8 2 20 9 0 0 9 1 10 10 0 0 |
|
|
|
|
|
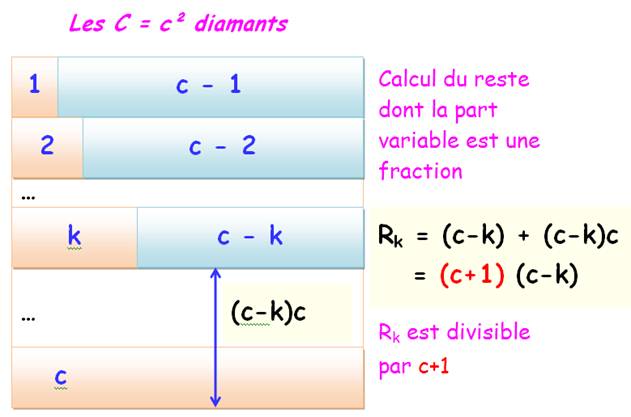
La flèche
indique que l'aire sous-jacente vaut: largeur (c-k) fois longueur (c). Bilan Un carré C = c² peut
se partitionner en une somme de c termes dont chacun est la somme de deux
termes: k et c – k. Au rang k, le reste à partitionner est divisible par c +
1. |
|
![]()
|
Retour |
|
|
Voir |
|
|
DicoNombre |
|
|
Cette page |
![]()