|
|||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Nombres triangulaires = double d'un triangulaire: Tn
= = 2Tm Nombres
triangulaires = nombre pronique: Tn = a(a+1)
6, 210,
7140, 242556, 8239770, 279909630, 9508687656, 323015470680, 10973017315470,
372759573255306, 12662852473364940, 430164224521152660, 14612920781245825506,
496409142337836914550, 16863297918705209269200, … Les
six seuls nombres triangulaires, produit de trois nombres consécutifs: Tn = a (a + 1) (a
+ 2)
Nombres
triangulaires = x! / y! 6, 120,
210, 990, 7140, 185136, 242556, 2162160, 8239770, 258474216, 279909630,
9508687656, 323015470680, 10973017315470, 372759573255306, 12662852473364940,
430164224521152660, 14612920781245825506, 496409142337836914550, … Exemples:
120 = 5! = 6! / 3! 210 = 7!
/ 4! 990
= 11! / 8! Cas triviaux: 7 = 7! /
6! n = n! / (n-1)! Cas spécial: 120 est à la fois le produit de trois et de
quatre nombres consécutifs. C'est le seul cas pour quatre consécutifs. Commentaires: si la différence entre les deux
factorielles est 3, on retrouve la propriété précédente: 120 = 6! / 3! = 6 x
5 x 4. |
|||||||||||||||||||||||||||||||||||||||||||||
Voir Nombres carrés / Nombres pentagonaux / Fonctions
génératrices des polygonaux
![]()
|
n |
Tn = ½ n ( n + 1 ) |
T10
= ½
10 (10+1) = 5 x 11 = 55 |
|
|
|
|||
|
n n+1 |
Tn = Tn–1
+ n |
T11 = 55 + 11 = 66 |
|
|
|
|||
![]()
|
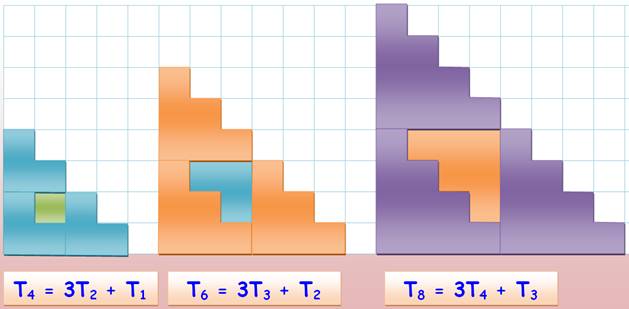
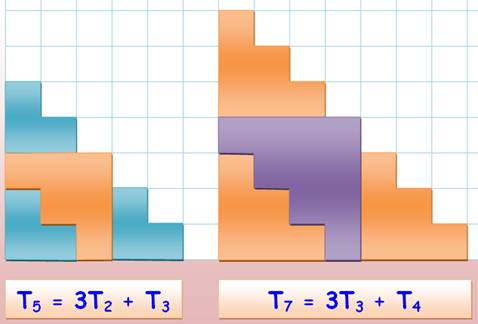
2n |
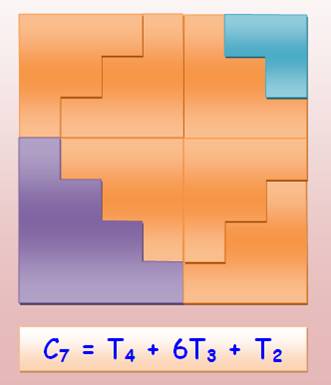
T2n = 3Tn + Tn–1 |
T6 = 3 x T3 + T2 = 3 x 6 + 3 = 21 |
|
Démonstration 2 { 3Tn + Tn-1 } = 3n (n + 1) + (n – 1)n = 3n² + 3n + n² –
n = 4n² + 2n = 2n (2n+1) = T2n |
||
Autres propriétés des triangulaires
|
N |
N = Ta + Tb + Tc |
5 =
3 + 1 + 1 12
= 10 + 1 + 1 83
= 45 + 28 + 10 |
|
|
||
![]()
|
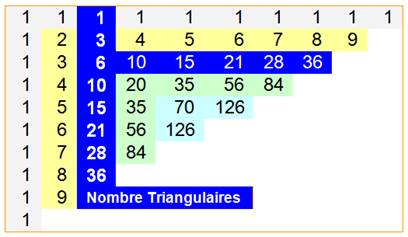
Pascal |
|
|
|
|
|
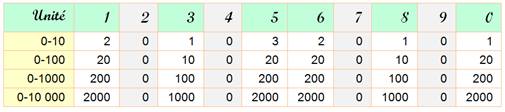
Unité |
Quantité de fois
l'unité selon la puissance de 10
Exemple:
parmi tous les nombres triangulaires pour n de 0 à 100, il y en a 20 qui se
terminent par 1. |
|
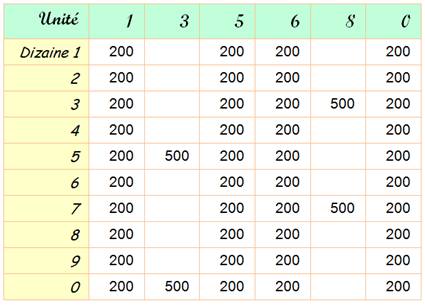
Dizaine |
Quantité de fois la
dizaine selon l'unité pour n de 0 à 10 000
Exemple:
parmi tous les nombres triangulaires pour n de 0 à 10 000, il y en a 500 qui
se terminent par 35 et 500 par 03. |
![]()
|
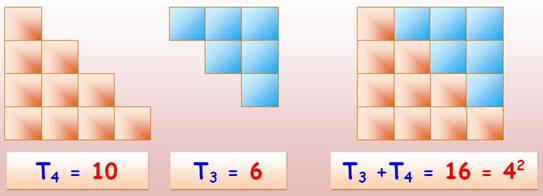
N2 |
N²
= Tn + Tn-1 |
1
+ 3 = 4 = 2² 3
+ 6 = 9 = 3² 6
+ 10 = 16 = 4² |
|
|
Voir Nombres
triangulaires carrés
&
Démonstration Tn + Tn-1= ½ n (n + 1)
+ ½ (n – 1) = ½ (n² + n + n² –
n) = 2 n² / 2 = n² Exemples de
partition d'un carré 100
= 10 ² = T10
+ T9 = 55 + 45 144
= 12 ² = T12
+ T11 = 78 + 66 Illustration
géométrique 16 = 4² = T4
+ T3 = 10 + 6
|
|||
|
N2 |
N² = 8 T + 1 (2n + 1)² = 8Tn + 1 |
8
x 1 + 1 = 9 = 3² 8
x 3 + 1 = 25 = 5² 8
x 6 + 1 = 49 = 7² |
|
Illustration
|
||
|
N2 |
(2n + 1)² = 8Tn + 1 = Tn-1 + 6Tn
+ Tn+1 |
7²
= (2x3+1)² = 8x6 – 1 = 49 = 3 +
6x6 + 10 = 49 |
|
|
||
|
N3 |
N3 = Tn² – Tn-1²
|
3² – 1² =
8 = 23 6² – 3² = 27 = 33 10²
– 6² = 64 = 43 |
|
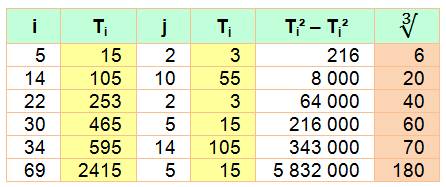
Démonstration Tn² - Tn-1² = [ 1/2 n
(n+1)]² – [ 1/2 (n-1) n]² = 1/4 n²
[(n+1)² – (n-1)²] = 1/4 n² x 4n = n3 Exemples
Note: seules quelques Ti²
– Tj² avec i et j non consécutifs sont des cubes:
|
||
|
N3 |
Nn3 - Nn-13 = 6 Tn-1 + 1 |
83
– 73 = 512 – 343 =
6 x T7 + 1 =
6 x 28 + 1 =168 + 1 =
169 |
|
Démonstration Nn
3 – Nn-1 3
= N3 – (N – 1)3 = N3 – (N3
– 3N² + 3N – 1) = 3N² – 3N + 1 = 3 (N² – N) + 1 = 6Tn + 1 |
||
|
Autres formules
montrant la divisibilité avec les cubes
Voir Divisibilité par 6 |
||
![]()
|
N4 |
N4
= TN (N – 1) – 1 + TN (N + 1) – 1 |
44
= 256 = T4x3 - 1 + T4x5 -1 = T11 + T19 = 66 + 190 = 256 |
|
Exemples
|
||
|
T² |
Tn2
+ Tn-12 = Tn²
|
6² + 3² = 45 10²
+ 6² = 136 |
|
|
Tn+12 – Tn2
= (n + 1)3 |
10²
– 6² = 64 = 43 |
||
Bilan
|
Un nombre triangulaire est le demi-produit de deux nombres consécutifs. Ils sont tous dans la deuxième colonne du triangle de Pascal. Ils sont toujours terminés par 0, 1, 3, 5, 6 ou 8. Les nombres triangulaires, du fait de leur "géométrie", se prêtent à de nombreuses combinaisons. On retiendra:
|
![]()
|
Suite Nombres
triangles |
|
|
Voir Nombres géométriques |
|
|
Voir |
|
|
DicoNombre |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Geometri/NbTrianC.htm |
![]()