|
||||||||||||||||||||||||||||||||||||||||
![]()
|
Nombre
45 Examen
des nombres divisibles par 45 ou par 5 et par 9. Combine ? |
|
Retour Pages
complètes sur le nombre 45
|
|
||
|
Une
énigme classique consiste à demander combien de nombres sont divisibles à la
fois par 5 et par 9 dans une plage donnée de nombres. Par
exemple, combien pour les nombres commençant par 123 et comportant trois
autres chiffres à droite ? |
Divisibilités
Exemple: 123
120, 123 930 |
|
Voir Divisibilité
par 5 / Divisibilité
par 9
Nombres aa..abb…b
divisibles par 45

Voir
Énigme
relative à de tels nombres / Brève
153
|
|
||||
|
Deux chiffres |
2 |
45 et 90 |
||
|
Trois chiffres |
20 |
En noir les nombres dont la somme des chiffres
est 9 et en rouge ceux avec la somme 18. Tableau suivant, en bleu les sommes 27. |
|
|
|
Quatre chiffres |
200 |
|
||
|
|
|||
|
Méthode directe Elle consiste à compter
combien de fois il y a d'intervalles de 45 dans la plage considérée.
Autrement-dit, faire la division. |
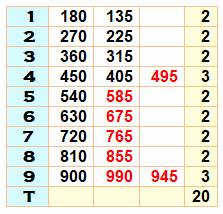
Exemple: Sur la plage des nombres de 1 à 1000, il ya a 22
fois un intervalle de 45. Ce résultat confirme le décompte vu plus haut: 2
nombres à deux chiffres et 20 à trois chiffres, soit un total de 22. Note: le nombre zéro est divisible par 45, non compté
ci-dessus. |
|
|
|
Méthode par raisonnement On peut également chercher
via la divisibilité. |
Exemple simple De 100 à 999, il y a 90 nombres qui se terminent
par 0. Pour obtenir la divisibilité par 9, les deux
premiers chiffres doivent totaliser 9: 1+8, 2+7, etc. soit 9 additions; ou
18: 9 + 9. Ce qui donne un total de 10 additions. De 100 à 999, il y a 90 nombres qui se terminent
par 5. Pour obtenir la divisibilité par 9, les deux
premiers chiffres doivent totaliser 4 ou 13. Ce qui donne 10 additions. Total: 10 + 10 = 20 multiples de 45 dans la plage
100 à 900. Exemple plus risqué Pour la plage 1000 à 9999, vous observerez que le
tableau ci-dessus montre deux intrus en bleu à droite. Pas si évident à
détecter sans faire un bilan minutieux |
||
|
Formulation |
Quantité de nombres divisibles par 5 et par 9
dans la plage des 10k:
Exemple: de 1000 à 9999
=> Q = 2x102 = 200 Quantité à partir de 0:
Exemple: de 1 à 9999
=> Q = 222 |
||
|
Énigme 1 avec 123 À
123 on ajoute trois chiffres à droite (123xyz). Combine de tels nombres sont
divisible par 5 et par 9. Solution Cas
où z = 0, alors x+y = 3 ou 12 => 030, 120, 210, 300, 390, 480, 570, 660,
750, 840, 930 => 11 cas Cas
où z = 5, alors x+y = 7 ou 16 => 075, 165, 255, 345, 435, 525, 615, 705,
795, 885, 975 => 11 cas Total 22 cas Énigme 2 avec 126 (somme 9) On
dénombre la même quantité de cas, avec un cas supplémentaire car 1 + 2 + 6 =
6 => 126000 est divisible par 45 Total 23 cas Énigme 3 avec 130 (somme 9 avec le 5 des unités) Cas
particulier en plus: 130005. Avec
z = 0 => xy = (05, 14, 23, 32, 41, 50, 59, 68,
77, 86, 95) = >11 cas Avec
z = 5 => xy = (00,
09, 18, 27, 36, 45, 54, 63, 72, 81, 90, 99) = > 12 cas Total 23 cas Quelques cas (100 => 22, 103
=> 23, 108 => 23, 111 => 22, 222 => 22, 333 =>23, 999 =>
23) |
|
|
||
|
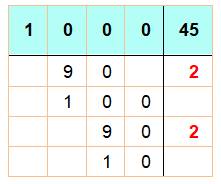
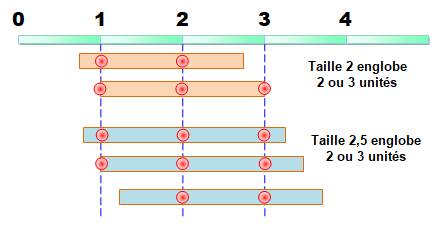
Avec un
intervalle de D fois u (l'intervalle unitaire), on englobe k ou k+1
intervalle unitaire selon que varie de D = ku
compris à (k – 1)u non compris. Dit-autrement
pas de déductions trop hâtives. |
|
|
|
|
||
|
Dans la plage des
nombres de 1 à 10n, il y a exactement Q nombres divisibles par k,
avec: Q = quotient de 10n / k sauf lorsque le
reste est nul alors, il y en a un de moins. |
Exemples Pour la plage 1 à 999, avec k
de 123 à 126
|
|
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
|
|
|
Cette Page |
![]()