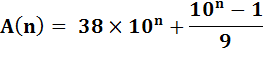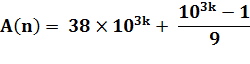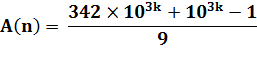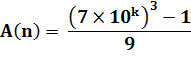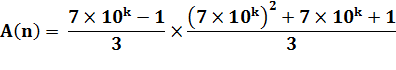Nombre 38 et les suites en 381 3811 38111 etc

NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 27/03/2016 Orientation générale DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique
	Nombres
Débutants Nombre	Insolites / Divers				Glossaire Nombre
INDEX Nombre Formes et motifs	Nombre 33	Nombres 37 et 38	Nombre 42	Nombre 100
	Terminale S	Sommaire de cette page >>> Approche >>> Formulation >>> Propriétés utilisées >>> Suite en 371 – Démonstration >>> Suite en 381 – Démonstration >>> Point et généralisation – Suites en Nddd… >>> English corner

Nombres 37 & 38

et suites infinies

de nombres composés

Les nombres 37 et 38 suivis de "1" sont tous composés quelle que soit la quantité de "1". La suite en 371 … est la plus petite avec des "1".

Il existe aussi une infinité de telles suites ayant une autre racine (R) que 37 ou 38 et ayant une terminaison (d) autre que 1. Alors d vaut {1, 3, ou 9} ou, d peut être un nombre à plusieurs chiffres.

Retour DicoNombre: Nombre 37 / Nombre 38

Tilt!

Le nombre 37 est bien connu comme facteur de

111 = 3 x 37.

Approche – Suite en A(1) = 371 et A(1) = 381

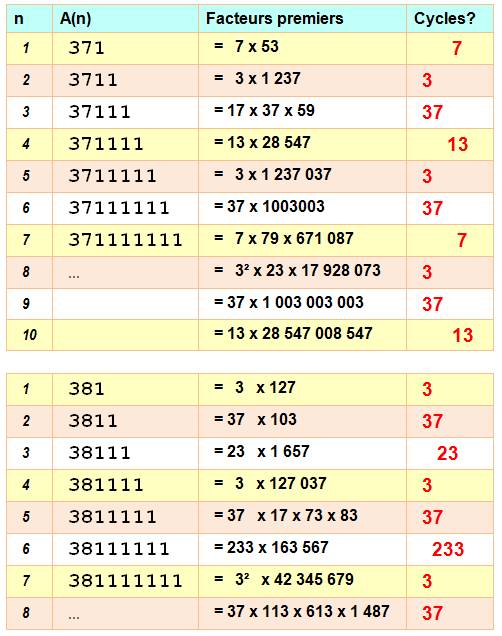
Avant toute tentative de démonstration, nous faisons une petite exploration numérique pour savoir où nous mettons les pieds.

Observations

Le tableau donne les valeurs de A(n) et de ses facteurs.

Tous ces nombres en 371 et en 381 sont composés.

Dans la colonne de droite on tente de déceler un cycle de répétition des facteurs les plus petits.

Pour la suite en 371, le cycle tournerait sur six valeurs:
{7, 3, 37, 13, 3, 37}.

Pour la suite en 381, le cycle tournerait sur trois valeurs:
{3, 37, x}.

Un tiers des valeurs ont un facteur x qui semble suivre le motif 23, 233 …

Formulation
D'abord, on peut écrire A(n) sous la forme d'une suite récurrente.	A(0) = 38 A(n+1) = 10 A(n) + 1
Ce qui donne effectivement:	38, 381, 3811, 38111 …
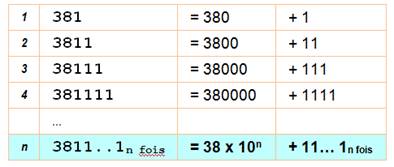
Ou, en décomposant les nombres en deux parties.
Il peut être utile de formuler aussi la partie en 111… (repunit) en observant que, par exemple: 111 = 999 / 9

Propriétés utilisées

Divisibilité par 3 si la somme des chiffres est divisible par 3.

Repunits: 111 = 3 x 37 et 111 111 = 7 x 15 873

Calcul de congruence (modulo ou restes de division)

Suite en 371 – Démonstration
La suite:
Selon nos observations, nous conjecturons que tous ces nombres sont divisibles par	{3, 7, 13 ou 37}
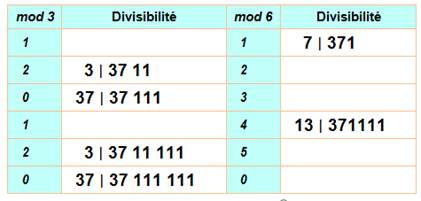
Divisibilité par 3 lorsque n = 3p + 2 Propriété: 111 = 3 x 37 0 mod 3	Ex: 3711 = 3 x 1 237 3711 111 = 3 x 1 237 037 En effet la somme des chiffres est divisible par 3. Démo en mod 3 A(n) est divisible par 3 pour n = 3p + 2
Divisibilité par 37 lorsque n = 3p Propriété: 111 = 3 x 37 0 mod 3	Ex: 37111 = 37 x 1003 37111 111 = 37 x 1 003 003 Démo en mod 37 A(n) est divisible par 37 pour n = 3p
Divisibilité par 7 lorsque n = 6p + 1 Propriétés 111 111 = 7 x 15 873 371 = 7 x 53	Ex: 371= 7 x 53 371 111111 = 7 x 53 015 873 Démo en mod 6 A(n) est divisible par 7 pour n = 6p +1
Divisibilité par 13 lorsque n = 6p + 4 Propriétés 111 111 = 13 x 8 547 371 111 = 13 x 28 547	Ex: 371111 = 13 x 28 547 371111 111111 = 13 x 28 547 008 547 Démo en mod 6 A(n) est divisible par 13 pour n = 6p +4
Bilan Avec l'analyse de ces quatre cas, nous couvrons toutes les possibilités (cf. Tableau). Tous les nombres en 371, 3711 … sont composés.

Suite en 381 – Démonstration
La suite:
Selon nos observations, nous conjecturons que tous ces nombres sont divisibles par	{3, 37 ou un nombre en 23, 233 …}
Divisibilité par 3 lorsque n = 3p + 1	Ex: 381 = 3 x 127 381 111 = 3 x 127 037 En effet la somme des chiffres est divisible par 3. Démo en mod 3 A(n) est divisible par 3 pour n = 3p + 2
Divisibilité par 37 lorsque n = 3p + 2 0 mod 3	Ex: 3811 = 37 x 103 3811 111 = 37 x 103 003 Démo en mod 37 A(n) est divisible par 37 pour n = 3p + 2
Divisibilité par x lorsque n = 3p avec x = {23, 233, …} ? La tactique consiste à trouver une mise en facteurs de nombres entiers Propriété: (X³ – 1) = (X – 1) (X² + X + 1 )
Les deux facteurs sont bien des entiers car le numérateur est divisible par 3.	F₁ = 7 x 10^k – 1 1x1 – 1 = 0 mod 3 F₂ = (7 x 10^k)² + 7 x 10^k + 1 1 + 1 + 1 = 0 mod 3
Bilan Avec l'analyse de ces trois cas, nous couvrons toutes les possibilités. Tous les nombres en 381, 3811 … sont composés.	Note Les facteurs en F₁ sont bien (7 x 10 – 1) / 3 = 69 / 3 = 23 (7 x 10² – 1) / 3 = 699 / 3 = 233 etc.

Point et généralisation – Suites en Nddd…
En 2011, Lenny Jones donne une démonstration générale de cette propriété en prouvant que 37 est la plus petite valeur. Pour cela, il a recourt à des mathématiques avancées, et, malheureusement sans rendre publique sa démonstration (du moins, elle est payante) >>> Il me semble qu'il commence par faire appel au théorème des restes chinois, et ensuite …?		Il a montré que: 37 suivi de 1 forme une suite de nombres composés; 37 n'est pas la seule racine, mais elle est la plus petite (avec des "1"); il existe de nombreuses autres suites A = Rdddd… avec d = {3, 7 et 9} et telles que R et d sont premiers entre eux. Exemple 891 777 … (la démonstration est possible; elle est due à TD Noe)
John Grantham et al. ont généralisé cette propriété.		Ils démontrent que: d peut être un nombre à plusieurs chiffres; il y en a une infinité.
Exemples donnés par Stan Wagon.	4070333…. le plus petit avec 3; 891777…. le plus petit avec 7 (à confirmer); 10175999…. le plus petit avec 9 (à confirmer).
La démonstration pour un cas donné n'est pas toujours trouvée, voire faisable. Les amateurs de ce genre de suite sont contraints à l'exploration par ordinateurs.			Exemples Pour 851 77 … a été éliminé en trouvant un contre-exemple premier avec un nombre de 28899 chiffres

Notes

Pourquoi premiers entre eux? Parce que, sinon, la suite devient triviale.

357 = 350 + 7 = 7 x 50 + 7 = 7 x 51

3577 = 350 + 77 = 7 x 500 + 7 x 11 = 7 x 511

etc.

Pourquoi d n'est pas 2, 5, 6 ou 8? Du fait de la trivialité.

Les nombres terminés par ces chiffres sont tous divisibles par 2 ou par 5.

English corner

Jones proves that 38 is the smallest composite number that produces only composite numbers when 1 is repeatedly appended to it.

Jones asked about integers that yield only composites when a sequence of the same base-ten digit is appended to the right. He showed that 37 is the smallest number with this property when appending the digit d = 1. For each digit d {3, 7, 9} he also found numbers coprime to d that yield only composites upon appending d's.

Grantham et al. prove that: There are infinitely many positive integers k with gcd (k, 2.5.7.9) = 1, such that for any base-ten digit d, appending any number of d's to k yields a composite number.

Source: voir référence in fine

Merci à Bernard G. pour avoir contribué à mettre à jour cette page

Suite	Suite de nombres composés consécutifs Autres pages de découvertes sur les nombres insolites
Voir	Cent avec tous les chiffres Factorielle Puissance Puzzles – Index Nombres en 4 fois 4 – Énigme des quatre 4 Nombre 33 sur la calculette
DicoNombre	Nombre 37 Nombre 38 Nombre 42
Sites	When Does Appending the Same Digit Repeatedly on the Right of a Positive Integer Generate a Sequence of Composite Integers? – Lenny Jones – Accès payant Repeatedly Appending Any Digit to Generate Composite Numbers – Jon Grantham, Witold Jarnicki, John Rickert, and Stan Wagon – May 2014 OEIS A187078 Puzzle 614. Always composite by insertion – The prime puzzles and problems connection
Cette Page	http://villemin.gerard.free.fr/aNombre/Nb0a1000/N38.htm