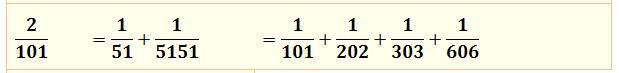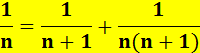|
|||||||||||||||||||||||||||||||||||
![]()
|
Nombre
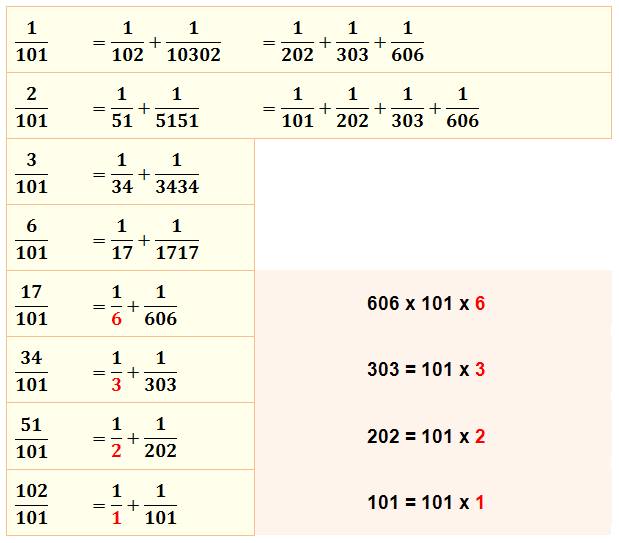
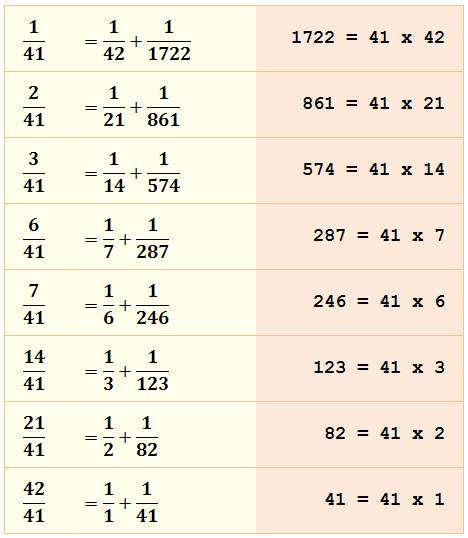
101 – Curiosités 1) Somme de
fractions à motifs esthétiques. Explication de la mécanique de construction
de tels motifs. >>> 2) Le nombre 101
est le seul de la forme 101010… à être premier. >>> |
|
|
|
|
(6 + 3 + 2 + 1) / 606 = 12/606 = 2/101.
|
|
|
|
|
|
Observations
|
|
|
|
|
|
17 = 1/2 + 33/2 = 1/3 + 50/3 = 1/4 +
67/4 = 1/5 + 84/5 = 1/6 + 101/6 = 1/7 + 118/7 = 1/8 + 135/8 = 1/9 + 152/9 =
1/10 + 169/10 = … |
|
|
|
|
|
|
|
|
|
|
|
|
|
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Cette page |
![]()