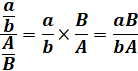Orientation Glossaire	Atlas / Nombres / Arithmétique / Opérations / Division Règle de trois / Pourcentage
Débutant DicoMot DicoNombre	FRACTION / RAPPORT

Index fractions >>>

Amusant, non?

Suite >>>

Histoire

Les fractions étaient appelées nombres rompus (Moyen Âge en Europe).

Définition

Division, partie d'un tout, portion.

Division de deux entiers a et b, notée a/b ou avec b non nul.

a et b sont les termes de la fraction.

a est le numérateur et b le dénominateur.

Se souvenir!

A	Numérateur	Nombre de parts
B	Dénominateur	Dénomination de la fraction: quantité totale de parts

Exemple: parmi les fractions en tiers (dénomination), je prends (un nombre de) deux parts; la fraction est 2/3, et 3 est le dénominateur et 2 le numérateur.

Voir Mnémotechnique

Langue

Fractionnaire: qui a la forme d'une fraction. Le quark a une charge électrique fractionnaire. Un exposant fractionnaire témoigne d'une racine.

Fractionnel: qui vise à la désunion d'un groupe, d'un parti, d'un syndicat.

Le rapport d'une grandeur à une autre est la fraction de l'un par l'autre. Ex: le rapport entre le mètre est le kilomètre est gal à 1/1000.

Fondement

On se propose de mesurer les longueurs de A et de B avec C:

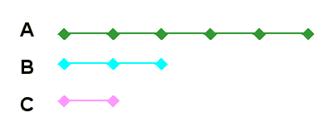
- Avec l'unité de mesure C

A vaut 5 C

B vaut 2 C

- On s'intéresse à ce que vaut A par rapport à B.

A	=	5C
B		2C

On énonce que A est les cinq demi de B.
sous-entendu avec l'unité de mesure commune C.

On écrit: A = 5/2 B.

Et aussi B est les deux cinquièmes de A.

On écrit: B = 2/5 A.

Nombres rationnels

Un nombre rationnel (ration = portion = fraction) est un nombre défini par une fraction. Exemples: 1/2 = 0,5 ; 2/3 = 0,666 … Ce nombre peut être périodique. Exemple: 1/7 = 0,142857 142857 …

Équivalence (Égalité)

Fractions égales ou (mieux) équivalentes. Pour que deux fractions a/b et c/d soient équivalentes il faut et il suffit que a.d = b.c On note a/b = c/d. Deux fractions équivalentes représentent le même nombre rationnel. Exemples: 0,5 = 1/2 = 2/4 Une fraction reste équivalente à elle-même si on multiplie numérateur et dénominateur par le même entier. Exemples: 2/3 = 4/6 = 6/9 = … Une fraction reste équivalente à elle-même si on divise numérateur et dénominateur par le même entier d, à condition que d soit un diviseur commun de a et b. Exemples: 25/100 = 5/20 = ¼

Irréductible Simplification	Si a et b sont premiers entre eux, la fraction a/b est irréductible. On ne peut plus la simplifier (ou la réduire). Le plus grand commun diviseur de a et b est alors 1. Exemples: 154/231 = 22/33 = 2/3
Dénominateur commun	On peut toujours trouver des fractions équivalentes ayant le même dénominateur à deux (ou plus) fractions. Ce dénominateur est le plus petit commun multiple des dénominateurs des fractions considérées Exemple: 1/20 & 1/12 PPCM (20,12) = 60 Fractions équivalentes avec même dénominateur: 3/60 & 5/60

Addition	Pour additionner (ou soustraire) deux fractions, il faut les réduire au même dénominateur et ajouter les numérateurs ainsi obtenus Somme des deux fractions ci-dessus: 8/60 = 2/15 D'une manière générale: a/b + c/d = (ad + bc) / bd
Multiplication	Pour multiplier deux fractions, on multiple numérateurs et dénominateurs Exemples: 3/20 x 5/12 = 15/240 = 16 D'une manière générale: a/b x c/d = ac / bd
Puissance	Pour élever une fraction à une puissance on élève numérateur et dénominateur à cette puissance D'une manière générale: (a/b)^n = a^n / b^n Toute puissance d'une fraction irréductible est une fraction irréductible
Division	Pour diviser une fraction par une autre on la multiple par la fraction inverse Exemple: 11/15 : 3/5 = 11/15 x 5/3 = 55/45 =11/9 D'une manière générale: a/b : c/d = a/b x d/c = ad / bc

Réduite	Une réduite est la fraction la plus proche d'un nombre réel, compte tenu du nombre de chiffres du dénominateur Exemple:355/113 Voir liens ci-dessous
Fraction généralisée ou Fraction à étage	Pour le numérateur, comme pour le dénominateur, on peut utiliser des fractions pour former une fraction généralisée. (a/b) / A/B) est une fraction généralisée ou fraction à étage. Une variété particulièrement importante de celles-ci est la fraction continue.	Exemple
Fraction décimale	Lorsque le dénominateur est une puissance de 10, il s'agit d'une fraction décimale. Exemples: 1/10 ; 1/1000000; 1/10^10
Convention	L'écriture a/1 représente l'entier a. La fraction 0/b représente le nombre 0. Par définition le cas a/0 est exclu. On peut écrire a/b = a.b^-1
Ensemble	Les fractions forment un corps. Q est le corps des fractions de Z dans R.

Anglais

Fraction a/b The number a is the numerator; the number b is the denominator. It is a proper fraction if a < b; and an improper fraction if a > b. Any number can be expressed as c + d/e, where c is an integer and d/e a proper fraction. This form c + d/ e is called a mixed fraction. Exemple: 7/2 = 3 + 1/2

FRACTIONS - Liens vers les pages de ce site

Généralités	Fractions – Développements Fractions – Débutants Fractions – Débutants avec briques Fractions – Découverte junior – Diaporama Fractions – Pour comprendre une fois pou toute avec la métaphore des bêtes à pattes - Diaporama Fractions en 6^e Fractions en 5^e Fractions avec les chiffres de 1 à 9, leurs sommes SOS - Je suis débutant – Général Division – Définition et propriétés de la division
Fractions Thèmes généraux	Classement des fractions Compter les fractions Développement décimal d'une fraction Multiplication des fractions Nombre fractionnaire ou rationnel Nombres irrationnel et fractions Nombres périodiques ou cycliques Nombres périodiques – THÉORIE Opérations sur les fractions – Exemples Quantité de fractions – Totient d'Euler
Type de fractions	Fractions continues Fractions de Stern-Brocot Fractions égyptiennes Fractions égyptiennes de somme 1 Fractions généralisées ou à étages Fractions irréductibles Fractions unitaires Fractions zigzag Série Harmonique Suites de Farey

Calculs	1/81= 0,0123456 … Nombre de Carroll 1/49 = 0,0204081632 … 1/7 = 0,142857 … Bœufs d'Hélios – Résolution Calcul de la fraction donnant 0,65 Calcul de Pi / 5 Comparaison entre fractions usuelles Énigmes avec des partages Extraction des chiffres de la période Fractions à étages Fractions avec les impairs consécutifs (= 1/3) Fractions et découpes successives Méthode de la fausse position Opérations sur les fractions – Exemples Réduction au même dénominateur Réduite d'un nombre irrationnel Règle de trois Simplification Somme d'inverses avec 101, 1001 … Somme d'inverses: 1/n = 1/(n+1) … Sommes d'inverses Sommes d'inverses quelconques Taux d'intérêts
Tables	Développement décimal des fractions – Période Fractions avec les nombres de 1 à 10 Fractions avec les nombres de 1 à 100 Fractions de somme 1 Fractions ordonnées en 1/k avec k de 2 à 18 Table des fractions égyptiennes
Construction	Partition en somme d'inverses Partition du cercle Théorème de Dirichlet: comment approcher un nombre irrationnel Distance entre 1/3 et 1/2 Fractions 1/2, 1/3, 1/4 …
Approximations par fractions	Année en fractions Développement p-adique Fractions donnant "e" Fractions donnant "Pi" Fractions donnant 1 avec les inverses des chiffres Fractions et nombre d'or

Fractions En savoir plus

Inverses et leurs sommes Série 1 + 2x + 3x² + ... Somme de deux inverses Sommes des inverses Suite aliquote Suite Harmonique Triangle de Leibniz

Fractions: Curiosités et Jeux

Un avec la plus petite fraction Faire 100 avec les chiffres de 1 à 9 en fractions Fractions pannumériques réduites en petites fractions Fractions en x /81 Fraction 2 avec carrés Fractions amusantes Fractions pannumériques minimales Fractions pannumériques qui donnent 100 Fractions qui engendrent les nombres successifs Fractions scandaleuses ou simplification illicite Autres fractions avec les chiffres du nombre Somme pannumérique de fractions Fractions et calendriers Produit de fractions (n-1) / n Distance entre 1/3 et 1/2

Fractions & Philosophie	La fraction américaine vue par Jacques Attali
Jeux	Don de Thot (Horus) => Partages de toutes sortes Partage du cercle

Cette page

http://villemin.gerard.free.fr/Referenc/Vocabula/GlosF/Fraction.htm