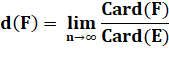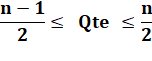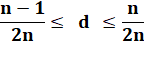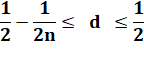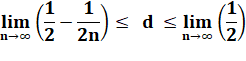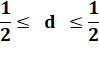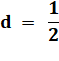|
Édition du: 16/11/2022 |
|
INDEX |
Notion d'INFINI |
||
Faites un double-clic pour un retour en haut de page
![]()
|
Densité naturelle ou asymptotique d'un ensemble Densité: rapport entre
la quantité d'éléments choisis dans un ensemble et la quantité totale des éléments de
l'ensemble. Densité asymptotique: valeur
de ce rapport quand la quantité d'éléments tend vers l'infini. Par exemple: la densité asymptotique de
l'ensemble des nombres pairs (ou des nombres impairs) est égale à 1/2. Notion qui
appartient à la théorie probabiliste des nombres. Basée sur les axiomes de Kolmogorov, fondements de la
théorie des probabilités
(1933). On dit aussi: densité naturelle ou densité arithmétique. |
||
|
|
Sommaire de cette page >>> Densité asymptotique >>> Exemple de calcul – Nombres pairs >>> Quelques ensembles >>> Historique
|
Débutants Glossaire |
|
Approche Définie intuitivement, la densité est toute quantité conçue pour décrire
la manière dont les éléments d'un ensemble sont répartis dans un ensemble de
référence. Nous nous intéressons ici à la densité d'ensembles d'entiers positifs
par rapport à l'ensemble de tous les entiers positifs. Il existe diverses mesures de densité de suites entières. Nous
abordons le cas de la densité asymptotique. |
||
|
Densité naturelle Possibilités de mesurer la taille d'un
sous-ensemble de l'ensemble des nombres naturels. Idée de la concentration de certains nombres
lorsqu'on se dirige vers l'infini. Définition Définition analogue à celle d'une probabilité: Si on choisit un nombre k dans l'ensemble E = {1
à n}, la probabilité qu'il appartienne aussi au sous-ensemble F est le
rapport entre le nombre d'éléments de F dans {1, n} au nombre total
d'éléments dans {1, n}. Pour n tendant vers l'infini, si la probabilité
tend vers une certaine limite cette limite est appelée la densité asymptotique de F. |
Exemple On remarque qu'il y a plus d'entiers positifs que
de carrés
parfaits entre 1 et n. Pourtant, il y a bien une infinité de chaque type
jusqu'à l'infini. Les deux ensembles – entiers et carrés – sont infinis et dénombrables
et peuvent donc être mis en correspondance biunivoque. Cependant, il y a de moins en moins de carrés
lorsque n est de plus en plus grand. La limite de cette densité tend vers 0. |
|
|
Valeurs Par définition un ensemble contient un seul
représentant de chaque élément (sinon c'est une liste). Si E comme F n'ont pas de répétitions, alors le
rapport des quantités d'éléments est toujours inférieur ou égal à 1. |
Limite du ratio des cardinaux
Note: pour les
experts, se reporter aux définitions et explications plus précises. |
|
|
Existence Une suite possède une densité asymptotique si et
seulement sa somme avec la densité de la suite complémentaires vaut 1. |
Condition d'existence: d(F) + d(F)C = 1 |
|
|
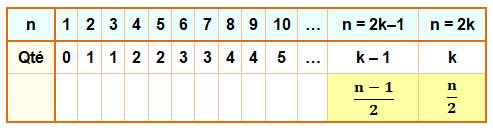
Prenons l'ensemble des nombres entiers. Et notons la quantité de nombres pairs en dessous
de chaque nombre. |
|
||
|
Cette quantité est cadrée: valeur minimale et
valeur maximale. En prenant le ratio par rapport à n, en fait, la
densité. |
|
||
|
Puis le passage à la limite, en fait, la densité
asymptotique. |
|
||
|
Soit sa valeur limite. |
|
||
|
Nombres entiers (de 1 à l'infini) |
d = 1 |
|
|
Nombres entiers de 1 à 1000 (ou autre nombre) Cas de tous les sous-ensembles finis |
d = 0 |
|
|
Nombres pairs
ou impairs |
d = ½ |
|
|
Nombres multiples
(m fois) d'une suite de densité D |
d = D / m |
|
|
Nombres d'une suite arithmétique
de raison r |
d = 1/r |
|
|
Nombres non membres d'une suite arithmétique de
raison r Propriété générale pour les ensembles
complémentaires |
d = 1 –
1/r |
|
|
Nombres d'une suite géométrique |
d = 0 |
|
|
Nombres carrés, cube, … |
d = 0 |
|
|
Nombres premiers |
d = 0 |
|
|
Nombres abondants |
0,2474
< d < 0,2480 |
|
|
Nombres sans facteurs
carrés |
d = 6 /
π² |
|
|
Nombre dont le développement
décimal commence par 1 |
d indéfini
entre 1/9 et 5/9 |
|
|
Nombres entiers qui, écrits en binaire,
ont un nombre pair de chiffres |
d
n'existe pas |
|
|
Au début du XXe siècle, Lev Genrichovitch Schnirelmann
(mathématicien russe) s'intéresse à la théorie générale de la densité des
suites numériques. Il introduit une mesure formelle de la densité des
nombres. Vers 1930, Paul Erdös (mathématicien hongrois) travaille sur les
nombres abondants et s'intéresse à l'étude de la densité asymptotique de
nombreuses suites. Il est suivi par H. Davenport, A. Besicovitch, F. Berhend,
S. Chawla, et bien d'autres. Ils étudient notamment: les multiples, les
suites primitives et les nombres à facteurs particuliers (k-free integers). En 1964, Niven et Zuckerman calculent la densité asymptotique d'une
suite arithmétique. En 1967, Ralph Alexander présente une technique de calcul qui se
révèle performante. En 1972 – Gustave C. Pekara publie The
asymptotic density of certain integer sequences. |
Haut de page (ou
double-clic)
![]()
|
Retour |
|
|
Suite |
|
|
Livre |
|
|
Sites |
|
|
Cette page |