NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 14/11/2022 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Nombres
Débutants Nombres	INFINI – Général				Glossaire Nombres
INDEX Nombres	Index infini		Introduction	Dénombrable
	Débutant		Types	Densité
	Historique		Transfinis
		Sommaire de cette page >>> Nombres >>> Escalier >>> Demi-cercle >>> Cercles >>> Boules

Il faut imaginer Sisyphe heureux.

Albert Camus – Le mythe de Sisyphe

Sisyphe refuse de mourir. Il s'oppose eux dieux dont Thanatos. Il en sera puni et condamné à pousser un rocher sur une colline. Lorsqu'il approche du sommet, le rocher se met à redescende, et cela éternellement.

Odyssée - Homère

Voir Pensées & humour

INFINI – Approche

Tout nombre possède un successeur et cela aussi loin que je puisse l'imaginer, ou pas! Tellement l'infini ne se laisse pas facilement appréhender.

Le symbole pour représenter l'infini est un 8 couché:

Maths bien curieuses! Après de nombreuses leçons et exemples pour faire comprendre à un étudiant que: formule => Pour vérifier qu'elle a bien compris, je lui donne un autre exemple. Voyez le résultat: formule =>

Voir Pensées & humour / Expressions avec "infini"

APPROCHE de l'INFINI – NOMBRES
Nous savons que les nombres entiers sont en nombre infini. En effet, il en existe toujours un plus grand que les autres. Chacun des nombres entiers possède un carré. Les nombres carrés sont donc, eux-aussi, en nombre infini. Mais chacun est plus grand que le nombre dont il est le carré. Il y aurait plus de nombres carrés que de nombres entiers? Non! La même chose une infinité. >>> En mathématiques de l'infini, il faut bien admettre que les comparaisons sont délicates.	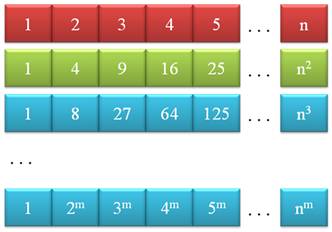Il y une infinité de nombres entiers, une infinité de carrés, une infinité de cubes, une infinité de puissances m. La même infinité.

APPROCHE de l'INFINI – L'ESCALIER
Quelle est la distance la plus courte pour aller de A à C ? le chemin ABC; le chemin en escalier; le chemin comprenant un grand nombre d'escaliers; le chemin comprenant une infinité d'escaliers; ou la diagonale AC. Oui ! Paradoxe qui semble montrer que la diagonale est égale à la somme de la longueur et de la largeur. Le seul moyen de lever le paradoxe est d'admettre différents niveaux d'infinis. Il y plus de points sur la diagonale que dans le nombre d'escaliers que l'on peut faire pour approcher la diagonale.	Parcours possibles
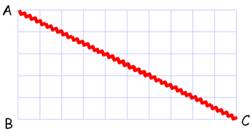
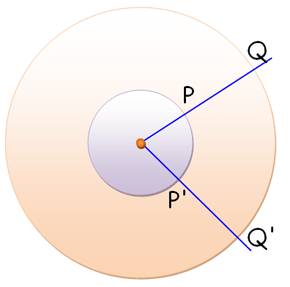
Soit la conclusion suivante: L'infini des nombres entiers est "moins riche " que l'infini de la quantité de points sur une droite.

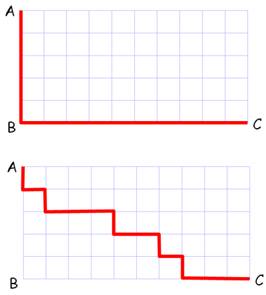
Voir Périmètre de l'escalier / Fractions en zigzag / Diagonale de Cantor / Marche de l'ivrogne

Cas du demi-cercle

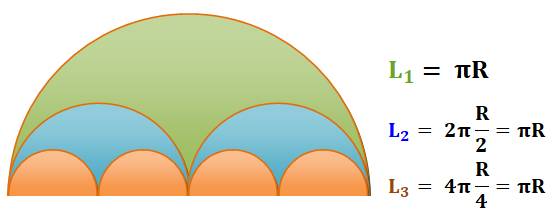
Les trois courbes ont même longueur. Et, ce serait le cas pour les courbes suivantes, en divisant à chaque fois le rayon par 2. À la limite, cette courge se rapproche du diamètre. On aurait donc D = 2R = 3,14 R, ce qui est absurde. Encore un paradoxe qui montre que le passage à la limite n'est pas licite. Les petits ponts se comptent en nombre entiers: 1, 2, 4, 16, … 2^k …, mais cela reste un nombre entier même à l'infini. Alors que la mesure du diamètre est en nombres réels. Et, il y a beaucoup plus de réels que d'entiers. Le paradoxe: l'un des infinis est plus grand que l'autre. Ce sont pourtant des infinis.

APPROCHE de l'INFINI – LE CERCLE
À première vue, le plus grand cercle (circonférence) devrait contenir plus de points que le petit. Or à chaque point P ou Q, il est possible d'associer un point P' ou un point Q': Il y a donc la même quantité de points sur les deux cercles. Et si le petit cercle était réduit à un point et le grand à un cercle de rayon infini ?

Voir Quantité infinie de points sur une droite

APPROCHE de l'INFINI – LES BOULES
Une expérience qui part dans une infinité de directions ! Une boule est tirée et elle est remise dans la boite en ajoutant une boule de la même couleur. Après un certain nombre de tirages on obtient une proportion de boules rouges et de boules bleues qui converge vers une valeur fixe. Cependant cette valeur est nouvelle à chaque fois que l'expérience est renouvelée.
Interprétation Le nombre de boules augmentant, la variance du nombre aléatoire qu'est la fréquence au coup suivant, connaissant la fréquence actuelle, diminue. L'amplitude du changement de la fréquence d'un coup à l'autre, peu à peu, s'amenuise. Il y a donc nécessairement convergence. Par contre, l'aboutissement est totalement imprévisible. La possibilité d'une valeur entre 0 et 1 est équiprobable.

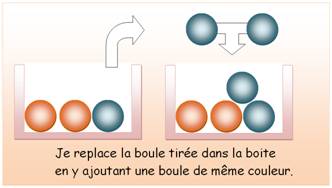
Voir Jeux / Statistiques

Suite	Types d'infinis Voir en haut de page
Voir	Arithmétique Finis et infinis Géométrie – Index
Cette page	http://villemin.gerard.free.fr/aNombre/NbInfini/Intro.htm