|
|||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Définition |
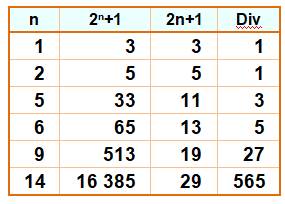
Nombres
de Curzon :
nombre n tel que: 2n + 1 est divisible par 2n + 1 |
|
Exemples |
|
|
Général |
Nom
donné par James J. Tattersall, Dans son livre: Elementary Number Theory in Nine Chapters,
Second Edition, Cambridge University Press. |
|
|
|
|
Ils sont 1 141
jusqu'à 10 000 1, 2, 5, 6, 9, 14, 18, 21, 26, 29, 30, 33, 41, 50, 53,
54, 65, 69, 74, 78, 81, 86, 89, 90, 98, 105, 113, 114, 125, 134, 138, 141,
146, 153, 158, 165, 173, 174, 186, 189, 194, 198, 209, 210, 221, 230, 233,
245, 249, 254, 261, 270, 273, 278, 281, 285, 293, 306, 309, 321, 326, 329,
330, 338, 341, 345, 350, 354, 366, 369, 378, 386, 393, 398, 405, 410, 413,
414, 426, 429, 438, 441, 453, 470, 473, 485, 498, 506, 509, 510, 525, 530,
534, 545, 546, 554, 558, 561, 581, 585, 590, 593, 606, 614, 618, 629, 638,
641, 645, 650, 653, 686, 690, 713, 714, 725, 726, 729, 741, 746, 749, 761,
765, 774, 785, 789, 798, 806, 809, 810, 813, 818, 833, 834, 846, 849, 854,
861, 866, 870, 873, 893, 894, 905, 930, 933, 938, 950, 953, 965, 966, 974,
986, 989, 993, 998, 1001, 1005, 1013, 1014, 1026, 1034, 1041, 1049, 1065,
1070, 1089, 1101, 1106, 1110, 1118, 1121, 1125, 1133, 1134, 1146, 1154, 1166,
1169, 1170, 1173, 1178, 1185, 1190, 1194, 1205, 1218, 1229, 1233, 1238, 1265,
1269, 1274, 1278, 1289, 1310, 1329, 1338, 1341, 1346, 1349, 1353, 1365, 1370,
1374, 1394, 1398, 1401, 1409, 1418, 1421, 1425, 1430, 1454, 1458, 1469, 1478,
1481, 1485, 1505, 1509, 1518, 1530, 1533, 1541, 1554, 1581, 1590, 1593, 1601,
1610, 1614, 1625, 1626, 1629, 1638, 1649, 1650, 1653, 1661, 1665, 1673, 1685,
1686, 1694, 1706, 1730, 1733, 1734, 1745, 1749, 1758, 1766, 1769, 1770, 1773,
1778, 1785, 1790, 1806, 1818, 1821, 1829, 1838, 1845, 1850, 1854, 1866, 1869,
1889, 1898, 1901, 1910, 1925, 1926, 1938, 1953, 1958, 1961, 1965, 1973, 1994,
2001, 2006, 2009, 2010, 2013, 2025, 2045, 2046, 2049, 2066, 2069, 2078, 2105,
2109, 2114, 2121, 2126, 2129, 2130, 2141, 2169, 2174, 2178, 2181, 2186, 2198,
2210, 2225, 2241, 2246, 2253, 2258, 2261, 2273, 2274, 2298, 2301, 2310, 2318,
2321, 2325, 2345, 2361, 2366, 2393, 2394, 2406, 2430, 2438, 2454, 2465, 2466,
2478, 2486, 2493, 2501, 2505, 2510, 2525, 2529, 2538, 2549, 2550, 2553, 2573,
2585, 2589, 2594, 2598, 2613, 2618, 2630, 2654, 2661, 2666, 2673, 2690, 2693,
2706, 2709, 2718, 2721, 2738, 2741, 2750, 2753, 2765, 2778, 2781, 2786, 2790,
2825, 2826, 2829, 2834, 2841, 2846, 2850, 2858, 2870, 2874, 2889, 2906, 2910,
2913, 2921, 2925, 2930, 2933, 2934, 2961, 2969, 2990, 2993, 3005, 3014, 3018,
3021, 3026, 3033, 3045, 3050, 3065, 3066, 3081, 3086, 3098, 3101, 3105, 3110,
3114, 3134, 3138, 3149, 3150, 3158, 3161, 3186, 3189, 3194, 3198, 3210, 3213,
3225, 3234, 3245, 3273, 3281, 3285, 3290, 3309, 3318, 3326, 3329, 3330, 3345,
3350, 3354, 3366, 3381, 3389, 3390, 3401, 3413, 3414, 3434, 3441, 3449, 3453,
3458, 3473, 3474, 3485, 3498, 3506, 3509, 3513, 3521, 3534, 3554, 3593, 3605,
3606, 3609, 3614, 3618, 3621, 3626, 3641, 3653, 3654, 3665, 3666, 3674, 3705,
3725, 3729, 3738, 3749, 3753, 3758, 3761, 3770, 3773, 3774, 3786, 3794, 3801,
3810, 3821, 3834, 3845, 3849, 3858, 3861, 3870, 3878, 3894, 3914, 3926, 3933,
3938, 3941, 3950, 3953, 3966, 3974, 3981, 4005, 4026, 4029, 4034, 4046, 4050,
4058, 4061, 4073, 4085, 4089, 4109, 4110, 4118, 4121, 4134, 4145, 4146, 4158,
4181, 4193, 4194, 4209, 4214, 4221, 4230, 4233, 4250, 4269, 4281, 4286, 4290,
4298, 4313, 4314, 4334, 4338, 4346, 4349, 4353, 4365, 4370, 4373, 4389, 4401,
4409, 4410, 4418, 4430, 4433, 4446, 4461, 4466, 4470, 4481, 4485, 4505, 4506,
4514, 4521, 4529, 4533, 4545, 4554, 4566, 4578, 4586, 4590, 4593, 4601, 4610,
4613, 4638, 4641, 4646, 4661, 4670, 4674, 4685, 4698, 4701, 4706, 4709, 4710,
4718, 4730, 4733, 4745, 4766, 4769, 4773, 4793, 4806, 4809, 4814, 4821, 4830,
4838, 4866, 4869, 4874, 4890, 4893, 4901, 4905, 4914, 4925, 4929, 4941, 4950,
4953, 4961, 4965, 4970, 4974, 4986, 5018, 5030, 5033, 5034, 5045, 5046, 5049,
5066, 5069, 5070, 5081, 5090, 5105, 5121, 5126, 5129, 5133, 5150, 5165, 5166,
5178, 5213, 5214, 5226, 5229, 5238, 5249, 5250, 5265, 5294, 5298, 5306, 5313,
5325, 5333, 5345, 5354, 5361, 5366, 5369, 5385, 5390, 5394, 5418, 5426, 5429,
5430, 5433, 5441, 5445, 5454, 5469, 5474, 5478, 5486, 5489, 5493, 5501, 5513,
5529, 5534, 5541, 5546, 5558, 5565, 5574, 5585, 5586, 5598, 5606, 5621, 5625,
5630, 5649, 5658, 5705, 5718, 5721, 5733, 5741, 5745, 5774, 5789, 5793, 5798,
5810, 5838, 5849, 5850, 5858, 5865, 5889, 5894, 5906, 5910, 5913, 5933, 5954,
5961, 5966, 5969, 5970, 5985, 5990, 5993, 6005, 6018, 6021, 6050, 6053, 6054,
6074, 6078, 6081, 6098, 6101, 6105, 6113, 6125, 6126, 6134, 6138, 6150, 6161,
6173, 6186, 6189, 6206, 6210, 6218, 6225, 6245, 6258, 6269, 6270, 6273, 6294,
6305, 6306, 6309, 6318, 6326, 6329, 6369, 6378, 6381, 6390, 6410, 6414, 6426,
6446, 6449, 6453, 6458, 6461, 6470, 6486, 6489, 6501, 6518, 6521, 6546, 6549,
6554, 6573, 6581, 6585, 6593, 6609, 6614, 6629, 6633, 6645, 6654, 6665, 6669,
6690, 6698, 6705, 6710, 6725, 6734, 6738, 6749, 6761, 6798, 6806, 6809, 6813,
6834, 6845, 6846, 6854, 6861, 6878, 6881, 6890, 6894, 6914, 6929, 6938, 6941,
6950, 6953, 6965, 6966, 6981, 6998, 7005, 7014, 7025, 7041, 7053, 7074, 7086,
7098, 7110, 7121, 7125, 7146, 7161, 7170, 7173, 7193, 7194, 7205, 7209, 7218,
7230, 7266, 7274, 7278, 7281, 7310, 7313, 7314, 7326, 7334, 7341, 7349, 7358,
7361, 7365, 7370, 7373, 7385, 7389, 7398, 7406, 7410, 7413, 7421, 7425, 7433,
7434, 7445, 7461, 7469, 7473, 7478, 7506, 7526, 7530, 7538, 7541, 7545, 7550,
7553, 7565, 7569, 7574, 7586, 7593, 7613, 7629, 7634, 7638, 7649, 7653, 7665,
7674, 7686, 7706, 7713, 7721, 7725, 7730, 7733, 7746, 7770, 7790, 7809, 7814,
7821, 7830, 7833, 7841, 7865, 7866, 7869, 7874, 7886, 7893, 7898, 7901, 7929,
7938, 7950, 7953, 7961, 7985, 7986, 8030, 8033, 8034, 8045, 8069, 8070, 8093,
8094, 8114, 8126, 8133, 8150, 8166, 8169, 8174, 8181, 8190, 8205, 8210, 8213,
8225, 8226, 8238, 8246, 8273, 8286, 8301, 8309, 8325, 8330, 8345, 8346, 8349,
8370, 8373, 8381, 8393, 8405, 8414, 8421, 8441, 8450, 8465, 8481, 8489, 8490,
8493, 8505, 8510, 8513, 8514, 8526, 8538, 8546, 8549, 8553, 8558, 8561, 8594,
8601, 8645, 8646, 8649, 8658, 8666, 8670, 8693, 8694, 8709, 8721, 8733, 8738,
8741, 8745, 8754, 8769, 8786, 8789, 8790, 8798, 8813, 8829, 8834, 8841, 8853,
8873, 8874, 8894, 8913, 8918, 8925, 8945, 8954, 8961, 8969, 8978, 8985, 8990,
8993, 8994, 9006, 9021, 9029, 9030, 9038, 9065, 9066, 9074, 9090, 9105, 9114,
9125, 9126, 9134, 9150, 9153, 9170, 9185, 9189, 9198, 9206, 9213, 9221, 9225,
9230, 9246, 9258, 9261, 9269, 9270, 9293, 9318, 9330, 9345, 9350, 9365, 9374,
9378, 9386, 9393, 9398, 9401, 9429, 9434, 9449, 9458, 9473, 9486, 9489, 9506,
9518, 9525, 9534, 9569, 9570, 9578, 9581, 9590, 9605, 9606, 9609, 9618, 9629,
9633, 9650, 9654, 9666, 9686, 9689, 9690, 9693, 9701, 9710, 9713, 9714, 9734,
9738, 9741, 9750, 9753, 9765, 9770, 9785, 9798, 9801, 9830, 9849, 9854, 9858,
9869, 9881, 9906, 9909, 9921, 9926, 9930, 9933, 9945, 9974, 9981, 9986, 9989,
9998 |
|
|
Anglais |
|
![]()
|
Voir |
|
|
Sites |
|
|
Cette
page |
![]()