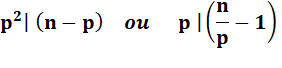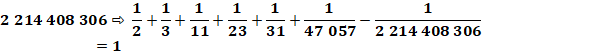NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 19/08/2020 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Types de Nombres
Débutants Général	Selon leurs diviseurs				Glossaire Général
INDEX Types de nombres	Parfaits	Semi-parfaits (SP)	SP Primitifs	SP Primaire
	Refactorisables	Pratiques	Abondant primitifs	Giuga
	Facteurs-Diviseurs	Intouchables	Curzon
		Sommaire de cette page >>> Nombre de Giuga >>> Propriétés >>> Liste

Famille	Nombre / Division / Diviseurs
Définition	Nombres de Giuga : nombre composé tel que la somme des inverses des facteurs diminuée de leur produit est égale à un nombre entier. Pour les douze nombres de Giuga connus, le nombre entier est 1.
Exemples	30 = 2 x 3 x 5

Propriétés

Général

Les nombres de Giuga ont été développés pour résoudre la conjecture de Giuseppe Guiga relativité à la primalité des nombres. Un nombre de Giuga est caractérisé par cette propriété: Pour chaque facteur p: Exemple avec 30: 2² divise 30 – 2 = 28 ou 2 divise 30/2 – 1 = 16 3² divise 30 – 3 = 27 ou 3 divise 30/3 – 1 = 9 5² divise 30 – 5 = 25 ou 5 divise 30/5 – 1 = 5

Liste des 12 nombres de Giuga connus
30, 858, 1 722, 66 198, 2 214 408 306, 24 423 128 562, 432 749 205 173 838, 14 737 133 470 010 574, 550 843 391 309 130 318, 244 197 000 982 499 715 087 866 346, 554 079 914 617 070 801 288 578 559 178, 1 910 667 181 420 507 984 555 759 916 338 506.
Formule développée

Anglais

Giuga numbers A composite number n such that each of its distinct prime factors p, we have p divides (n/p – 1).

Voir	Nombres refactorisables Diviseurs Factorielles Dénombrement – Combinatoire Compter les sous-ensembles Énigmes de pesées
Sites	Nombre de Giuga – Wikipédia Giuga numbers – Wolfram MathWorld OEIS A007850 – Giuga numbers: composite numbers n such that p divides n/p - 1 for every prime divisor p of n.
Cette page	http://villemin.gerard.free.fr/aNombre/TYPDIVIS/Giuga.htm