|
||||||||||||||||||||
![]()
|
NOMBRES PREMIERS Définition de paires de premiers consécutifs selon la
distance qui les sépare: jumeaux (2), cousins (4) et sexys (6). |
|
|
|
|
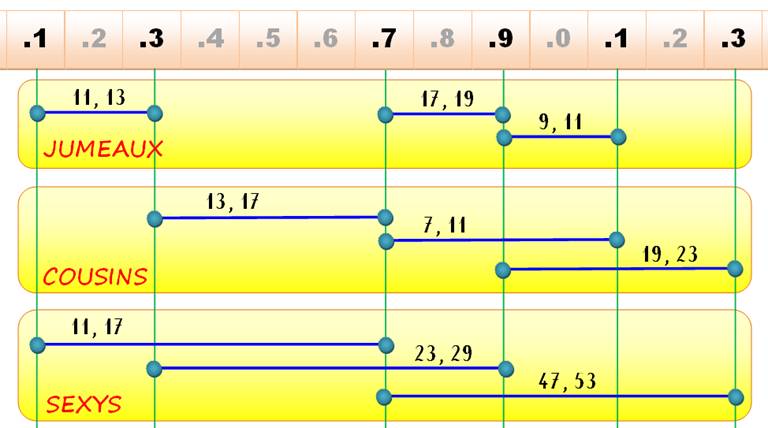
La figure montre les trois
configurations possibles pour les jumeaux
(distance 2), les cousins (distance 4) et les sexys (distance 6). Note: Contrairement à cette figure de principe, deux premiers ne sont
cousins ou sexys que s'ils sont premiers consécutifs;
il n'existe aucun autre nombre premier dans l'intervalle.
NB. La
barre des nombres (rose) montre les unités des nombres. On exclut le cas
particuliers des nombres de 1 à 10 (avec 2 et 5 qui sont premiers). Les
paires de nombres indiquées sont des exemples. Remarques utiles pour l'analyse de la succession des nombres premiers:
Conclusion: que les
paires soient jumelles, cousines ou sexies, au mieux seules trois paires (quadruplets) peuvent se
succéder, paires successives ou non. Suite >>> Démonstration: Pourquoi pas plus de trois
jumeaux d'affilé, au mieux. Un nombre premier
est en n + 1 o u 6n – 1. S'il est 6n + 1, les suivants sexys sont en 6n + 3,
celui-ci est divisible par 3 et n'est pas premier. S'il est 6n – 1, les suivants sexys sont en 6n + 1, 6n
+ 3, qui n'est pas premier. Pourquoi pas plus de trois
cousins d'affilé, au mieux. S'il est 6n + 1, les suivants sexys sont en 6n + 5, 6n
+ 9 celui-ci est divisible par 3 et n'est pas premier. S'il est 6n – 1, les suivants sexys sont en 6n + 3, qui
n'est pas premier. Voir Tableau >>> |
|
|
|
|
|
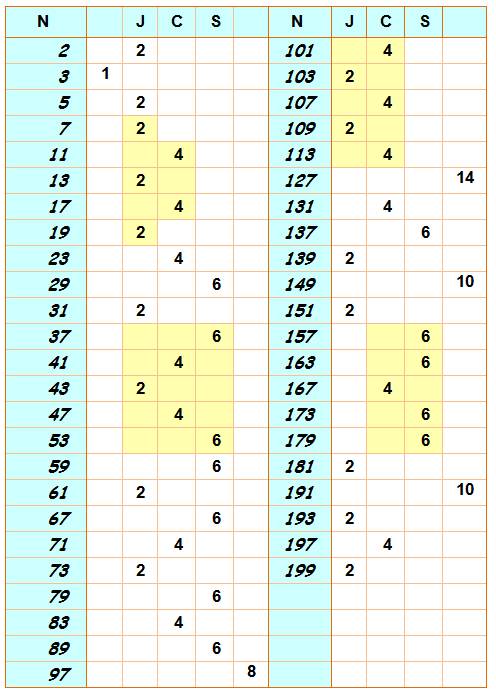
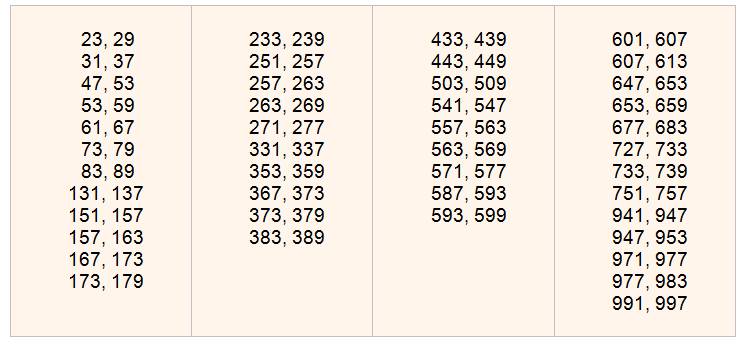
Le tableau donne les distances au précédent
nombre premier. De sorte que, par exemple, 29 est sexy avec
23.
|
|
En jaune, configurations sympathiques
Voir Barre magique des nombres premiers
|
|
||
|
|
Commentaire Initialisation. Préparation de trois listes pour
les jumeaux, cousins et sexys. Le premier nombre premier est initialisé à 2 et pp servira à conserver la mémoire du précédent
premier traité. Boucle d'exploration avec i comme numéro de
boucle. On stoppe la boucle (break) lorsque les nombres premiers dépassent 200. Calcul du prochain premier avec nextprime. Selon la distance (2, 4 ou 6), on remplit la
liste correspondante. Avec Maple, une liste est complétée en ouvrant
une liste J:= [
], en replaçant dedans la liste déjà connue op(J), et en précisant le nombre à ajouter p. À chaque itération, pp conserve la mémoire du
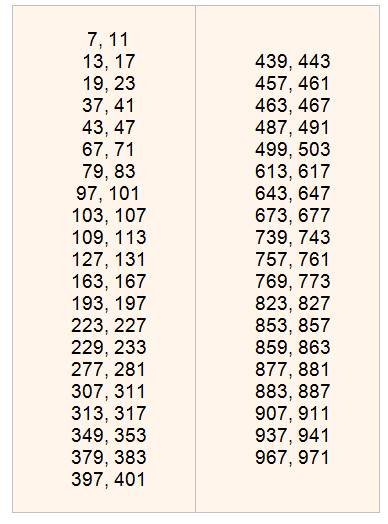
nombre premier p. En fin de travail, impression des trois listes. En bleu, les trois listes donnant le plus petits
des nombres jumeaux, cousins set sexys jusqu'à 200. |
|
Voir Programmation – Index
![]()
|
|
||
|
F |
Nombre / Diviseurs / Multiplicatif /
Premiers / … … / Quadruplet / Constellation |
|
|
Approche |
Soit trois cas: 1 et 3; 7 et 9 ; 9 et 1. |
|
|
Définition |
NOMBRES PREMIERS JUMEAUX
|
|
|
Propriétés |
du
moins, on le conjecture,
ce n'est pas prouvé.
|
|
|
Angl |
|
|
|
Voir |
||
|
|
|
|
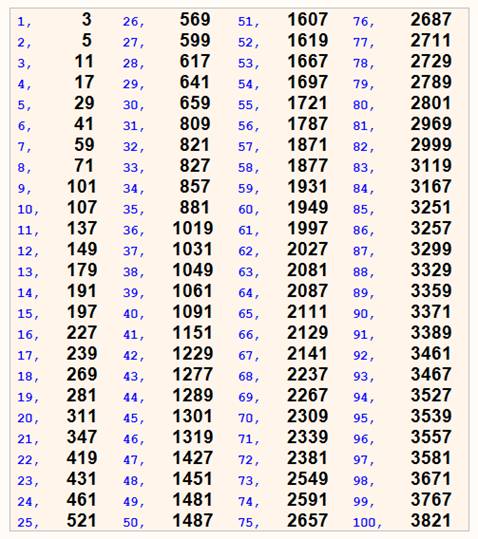
Les
200 du début de liste. On
donne le premier de la liste; le second est égal au premier +2 En
bleu, le rang de la paire.
|
|
|
|
||
|
Définition |
NOMBRES PREMIERS COUSINS
|
|
|
Rem |
7, 11 13, 17 19, 23 etc. |
|
|
Angl |
|
|
|
|
||
|
Définition |
NOMBRES PREMIERS SEXYS
(5,11), (7,13), (11,17), (13,19), (17,23),
(23,29), (31,37),
(37,43), (41,47), (47,53), (53,59), (61,67),
(67,73), (73,79), (83,89), (97,103), (101,107) … Note:
Certains
auteurs ne font pas cette distinction. |
|
|
Anglais |
|
|
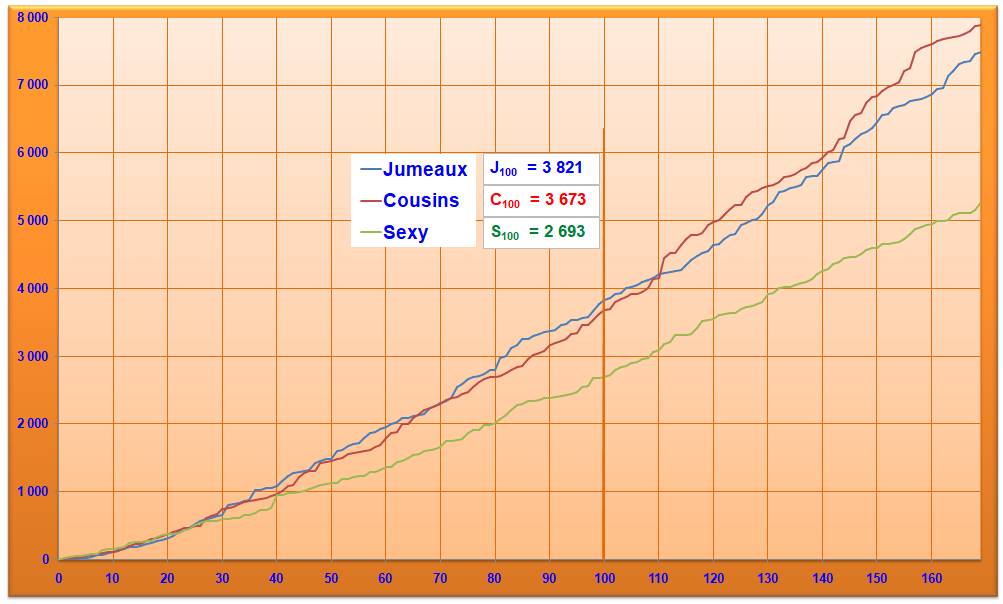
Rang des
nombres jumeaux, cousins et sexy
Avec exemple pour le
centième nombre de tête pour chaque famille
Quantité
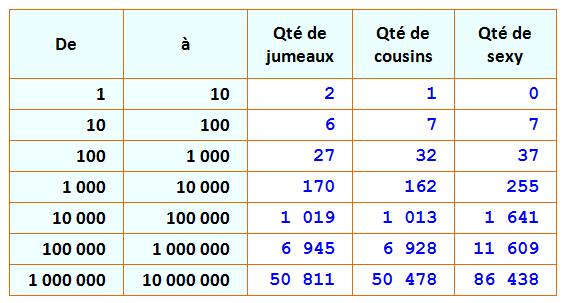
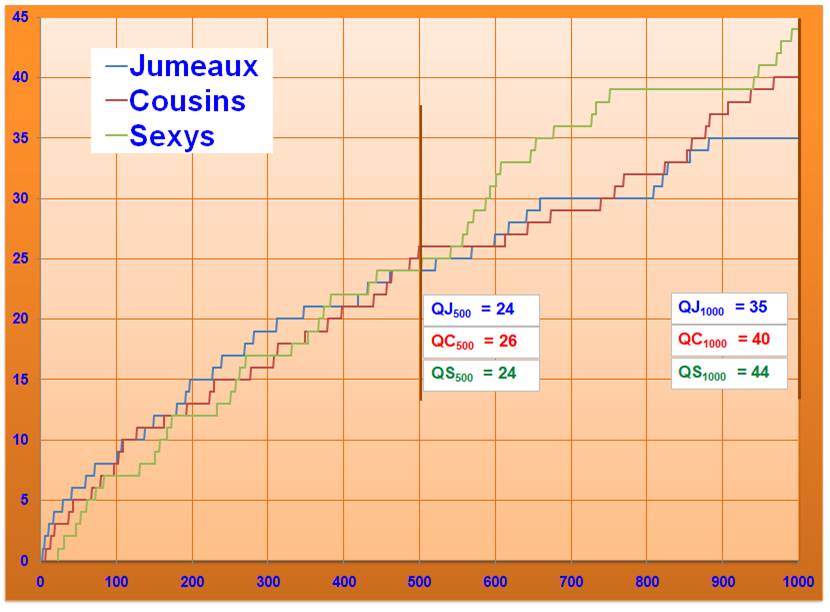
de nombres jumeaux, cousins et sexy jusqu'à n
Avec exemple pour n =
500 et n = 1000
Par exemple, il y a 44
nombre sexys jusqu'à 1000
![]()
|
Voir |
|
|
Cette page |
http://villemin.gerard.free.fr/aNombre/TYPMULTI/Premjume.htm
|
![]()