|
||||||||||||||||||||||||||||||||||||||||
![]()
|
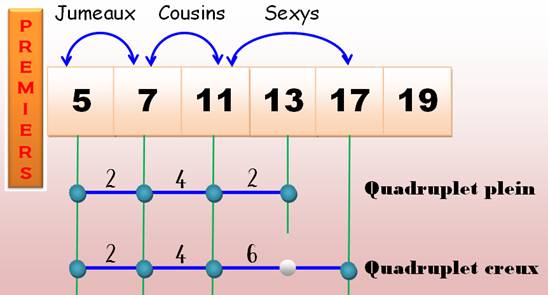
Nombres PREMIERS en CONSTELLATIONS Triplets et quadruplets On s'intéresse aux nombres premiers successifs pris par groupe de 3 ou 4. Quelles sont les configurations
possibles entre jumeaux,
cousins et sexys? Exemple: le
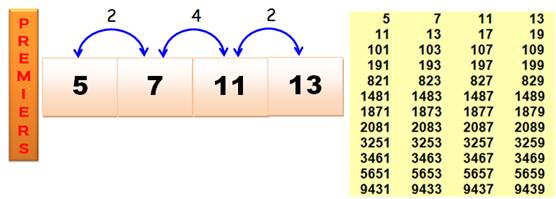
quadruplet: 101, 103, 107, 109 avec un espacement de 2, 4, 2 est de la forme
jumeaux, cousins, jumeaux. Conjecture des premiers
k-uples ou des constellations de premiers: émise par G. H. Hardy and J. E.
Littlewood en 1923 qui donne une estimation de la quantité de fois qu'une constellation de premiers se produit. |
|
|
|
|
Les nombres premiers pris par paires peuvent être jumeaux, cousins ou sexys selon leur éloignement. Voir les pages qui leurs sont
consacrées. Par famille, ils peuvent être en triplets, quadruplets, quintuplets, sextuplets …
On distingue les n-uplets pleins lorsque
tous les premiers sont présents et les n-uplets creux
lorsqu'il en manque. Exemple
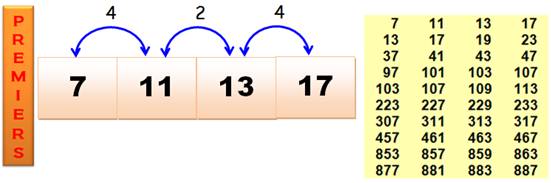
Deux notations pour un n-uplet, avec l'exemple du
quadruplet plein de la figure:
|
|
Voir Jumeaux, cousins, sexys –
Illustration
|
|
|
|
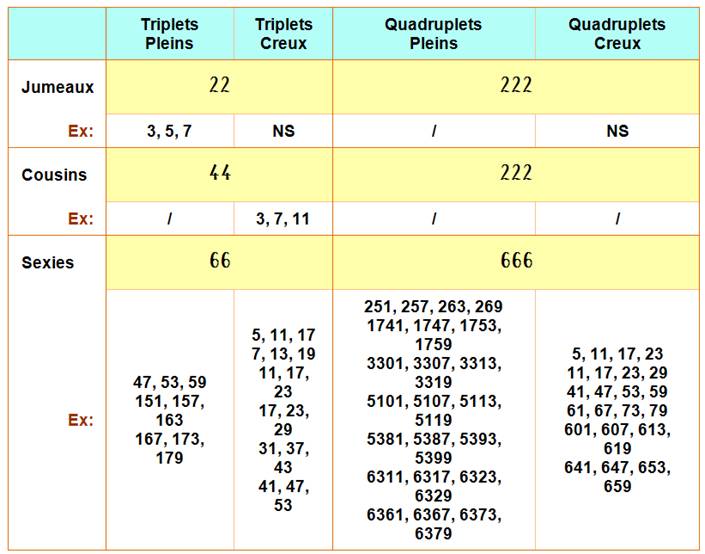
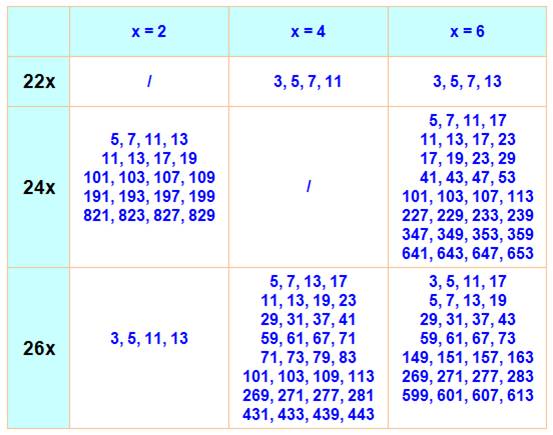
Ce que nous savons:
parmi les paires de nombres premiers jumelles, cousines ou sexies, seules
trois paires (quadruplets), au mieux,
peuvent se succéder, que se soient des paires successives ou non. Aucun que
l'on veut pour les sexys. Voilà le tableau récapitulatif des configurations pures possibles et impossibles.
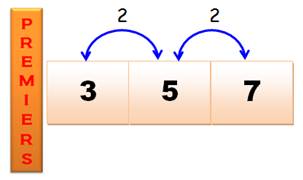
Par exemple: 3, 5, 7
sont les seuls trois (triplet) jumeaux se succédant (triplet plein). Pour le
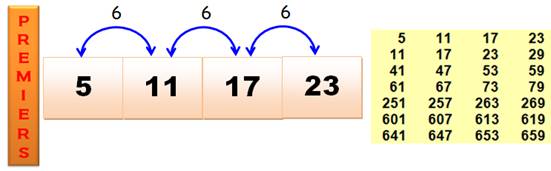
quadruplet 251, 257, 263, 269, l'espace entre les premiers est égal à 6 et
aucun premier n'est présent dans ces espaces. Le quadruplet
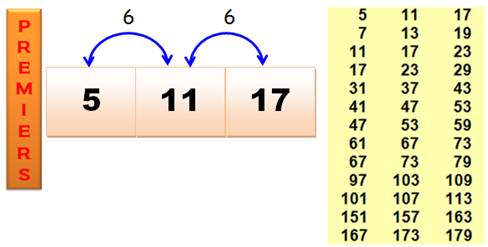
est plein. Pour le quadruplet 5, 11, 17, 23, l'espacement
est bien de 6, mais au milieu il existe des nombres premiers comme 7, 13 et
19. Le quadruplet est creux Le seul quintuplet avec écart de 6666 est 5, 11, 17, 23, 29
et il est creux (par exemple le 13 est au milieu). Maintenant
examinons les panachages entre jumeaux, cousins et sexys. |
|
|
|
||
|
Triplets
de jumeaux P, P+2, P+4 |
|
|
|
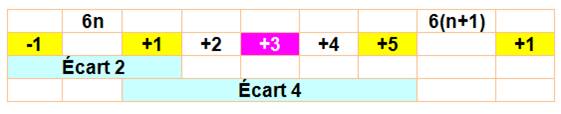
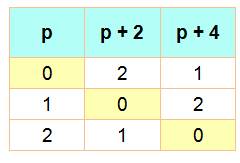
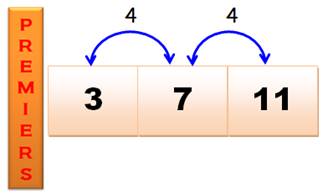
Unicité Tous les nombres premiers supérieurs à 3 sont de la
forme 6n – 1 ou 6n + 1.
Les seuls écarts possibles entre nombres premiers sont
2 puis 4. Mais jamais 2 puis 2. Il est donc impossible de trouver deux
premiers triplés. Configuration des
nombres premiers (En jaune position où un nombre peut être premier)
La position + 3 est impossible. Impossible de trouver
des triplets de jumeaux autre que 3, 5 et 7. Voir Illustration Preuve d'unicité de 3,
5 et 7 Si
p, p + 2 et p + 4 sont premiers, alors P = 3. Démontrez.
Voyons
ce qui se passe dans chacun des trois cas: Le
tableau montre que, quelle que soit la valeur du reste pour p, alors un des trois nombres
est divisible par 3, donc pas premier. Aucune
configuration, autre que p = 3, n'est compatible avec nos hypothèses. |
||
|
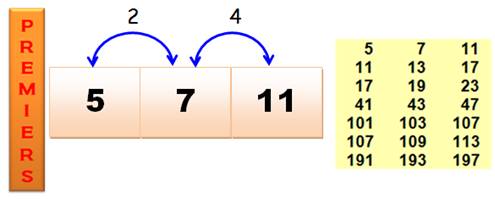
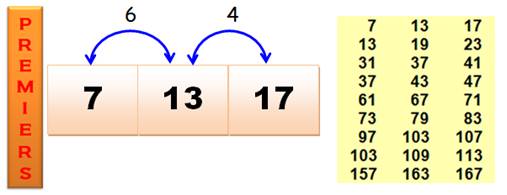
Triplets
de jumeau et cousin P, P+2, P+6 |
Liste pour n jusqu'à10 000 5, 11, 17, 41, 101, 107, 191, 227, 311, 347, 461,
641, 821, 857, 881, 1091, 1277, 1301, 1427, 1481, 1487, 1607, 1871, 1997,
2081, 2237, 2267, 2657, 2687, 3251, 3461, 3527, 3671, 3917, 4001, 4127, 4517,
4637, 4787, 4931, 4967, 5231, 5477, 5501, 5651, 6197, 6827, 7877, 8087, 8231,
8291, 8537, 8861, 9431, 9461. |
|
|
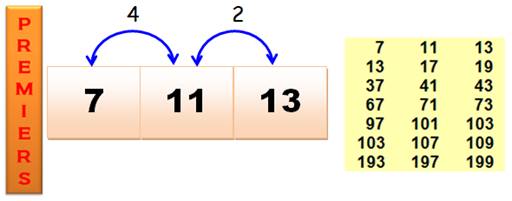
P, P+4, P+6 |
Liste pour n jusqu'à10 000 7, 13, 37, 67, 97, 103, 193, 223, 277, 307, 457,
613, 823, 853, 877, 1087, 1297, 1423, 1447, 1483, 1663, 1693, 1783, 1867,
1873, 1993, 2083, 2137, 2377, 2683, 2707, 2797, 3163, 3253, 3457, 3463, 3847,
4153, 4513, 4783, 5227, 5413, 5437, 5647, 5653, 5737, 6547, 6823, 7207, 7753,
7873, 8287, 8623, 9007, 9277, 9337, 9433. |
|
|
|
||
|
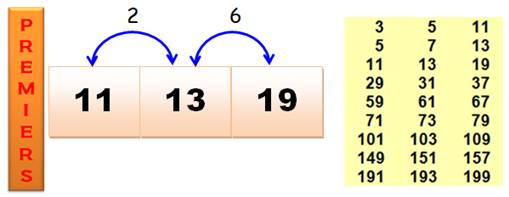
Triplets
de jumeaux et sexys P, P+2, P+8 |
Attention:
Les premiers ne sont pas consécutifs. Liste pour n jusqu'à10 000 3, 5, 11, 29, 59, 71, 101, 149, 191, 269, 431,
569, 599, 821, 1031, 1061, 1229, 1289, 1319, 1451, 1481, 1619, 1871, 2081,
2129, 2339, 2381, 2549, 2711, 2789, 3251, 3299, 3461, 3539, 4019, 4049, 4091,
4649, 4721, 5099, 5441, 5519, 5639, 5651, 5741, 5849, 6269, 6359, 6569, 6701,
6959, 7211, 8009, 8999, 9041, 9341, 9431. |
|
|
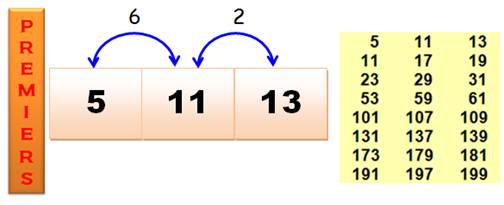
P, P+6, P+8 |
Liste pour n jusqu'à10 000 5, 11, 23, 53, 101, 131, 173, 191, 233, 263, 563,
593, 653, 821, 1013, 1223, 1283, 1481, 1601, 1613, 1871, 2081, 2333, 2543, 2963,
3251, 3323, 3461, 3533, 3761, 3911, 3923, 4013, 4211, 4253, 4643, 4793, 5003,
5273, 5471, 5651, 5843, 5861, 6263, 6353, 6563, 6653, 6863, 7121, 7451, 7481,
7541, 7583, 8081, 8423, 8831, 8963, 9413, 9431, 9623, 9851, 9923. |
|
|
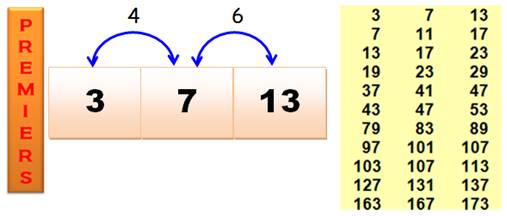
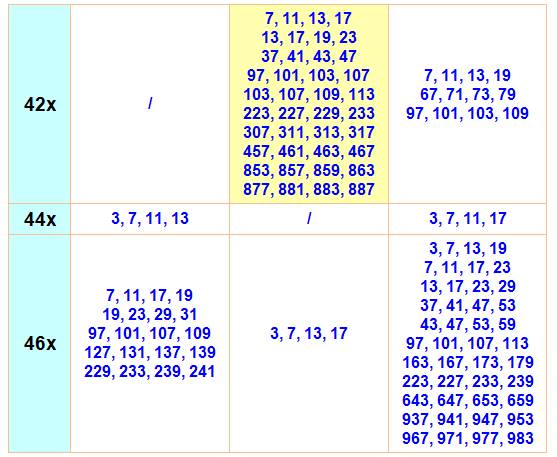
Triplets
de cousins et sexys P, P+4, P+10 |
Liste pour n jusqu'à10 000 3, 7, 13, 19, 37, 43, 79, 97, 103, 127, 163, 223,
229, 307, 349, 379, 439, 457, 499, 643, 673, 853, 877, 937, 967, 1009, 1087,
1093, 1213, 1279, 1297, 1423, 1429, 1483, 1489, 1549, 1597, 1609, 1867, 1993,
2203, 2347, 2389, 2437, 2539, 2683, 2689, 2833, 2953, 3079, 3319, 3457, 3529,
3613, 3793, 3907, 3919, 4003, 4129, 4447, 4513, 4639, 4783, 4789, 4933, 4999,
5077, 5227, 5647, 5839, 5857, 6043, 6823, 6907, 6967, 7243, 7477, 7537, 7573,
7639, 7873, 8233, 8287, 8419, 8689, 8737, 9199, 9463, 9619, 9739, 9829. |
|
|
P, P+6, P+10 |
Liste pour n jusqu'à10 000 7, 13, 31, 37, 61, 73, 97, 103, 157, 223, 271,
307, 373, 433, 457, 607, 733, 751, 853, 877, 1087, 1291, 1297, 1423, 1483,
1543, 1657, 1777, 1861, 1867, 1987, 1993, 2131, 2287, 2341, 2371, 2383, 2467,
2677, 2683, 2791, 2851, 3181, 3313, 3457, 3607, 3691, 4441, 4507, 4513, 4723,
4783, 4993, 5227, 5407, 5431, 5521, 5563, 5641, 5647, 5683, 5851, 6037, 6211,
6571, 6823, 6961, 6991, 7237, 7681, 7717, 7867, 7873, 7927, 8161, 8263, 8287,
8731, 8923, 9001, 9127, 9151, 9613, 9733, 9781. |
|
|
Triplets
de cousins P, P+4, P+8 |
|
|
|
Triplets
de sexys P, P+6, P+12 |
Liste pour n jusqu'à10 000 5, 7, 11, 17, 31, 41, 47, 61, 67, 97, 101, 151,
167, 227, 251, 257, 271, 347, 367, 557, 587, 601, 607, 641, 647, 727, 941,
971, 1091, 1097, 1117, 1181, 1217, 1277, 1291, 1361, 1427, 1447, 1481, 1487,
1601, 1607, 1657, 1741, 1747, 1777, 1861, 1867, 1901, 1987, 2131, 2281, 2371,
2377, 2411, 2671, 2677, 2687, 2707, 2791, 2897, 2957, 3301, 3307, 3457, 3527,
3631, 3727, 3911, 3917, 4001, 4007, 4127, 4451, 4507, 4591, 4637, 4651, 4787,
4931, 4987, 5101, 5107, 5297, 5381, 5387, 5407, 5431, 5437, 5471, 5557, 5641,
5647, 5737, 5801, 6067, 6257, 6311, 6317, 6361, 6367, 6857, 6971, 7207, 7517,
7577, 7817, 7867, 8081, 8111, 8231, 8707, 8741, 9001, 9337, 9391, 9461, 9467. |
|
|
|
||
|
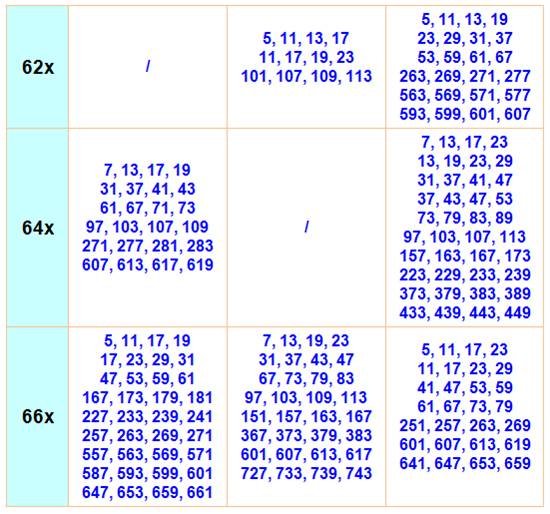
Quadruplets
P, P+2, P+6, P+8 |
|
|
|
Quadruplés ou
bijumeaux: deux paires de jumeaux successives. Les
deux nombres premiers du centre sont cousins (écart 4). Mis à part le premier quadruplé, les unités de tous les
autres sont de la forme: 1, 3, 7, 9 Il y a 11 quadruplés (plus un non générique) inférieurs
à dix mille. La somme des inverses des quadruplés converge vers 0,
87058 83800, la constante de Brun des
quadruplés. Ils sont tous de la forme: 30n + 11,
30n + 13, 30n + 17, 30n + 19 |
||
|
Quadruplets
(forme
inversée) P, P+4, P+6, P+10 |
Liste pour n jusqu'à10 000 7, 13, 37, 97, 103, 223, 307, 457, 853, 877,
1087, 1297, 1423, 1483, 1867, 1993, 2683, 3457, 4513, 4783, 5227, 5647, 6823,
7873, 8287. |
|
|
|
||
|
P, P+6 P+12, P+18 |
Aucun
en jumeaux et en cousins. Liste pour n jusqu'à10 000 5, 11, 41, 61, 251, 601, 641, 1091, 1481, 1601,
1741, 1861, 2371, 2671, 3301, 3911, 4001, 5101, 5381, 5431, 5641, 6311, 6361,
9461. |
|
|
Tous
les quadruplets jusqu'à 1000
|
||
|
|
||
|
Quadruplet en [1, 3, 7, 9] Quadruplets
qui apparaissent dans la même dizaine. Il
y en a une infinité. Programme Maple
Commentaires Le
principe consiste à tenir à jour un ensemble de quatre nombres premiers qui
se suivent. Pour
détecter la dizaine, on calcule d, la dizaine du premier dans la quadruplet,
et e, la dizaine pour le dernier. Voir Programmation – Index |
Les 39 jusqu'à 100 000 {2, 3, 5, 7} {11, 13, 17, 19} {101,
103, 107, 109} {191,
193, 197, 199} {821,
823, 827, 829} {1481, 1483, 1487, 1489} {1871, 1873, 1877, 1879} {2081, 2083, 2087, 2089} {3251, 3253, 3257, 3259} {3461, 3463, 3467, 3469} {5651, 5653, 5657, 5659} {9431, 9433, 9437, 9439} {13001, 13003, 13007, 13009} {15641, 15643, 15647, 15649} {15731, 15733, 15737, 15739} {16061, 16063, 16067, 16069} {18041, 18043, 18047, 18049} {18911, 18913, 18917, 18919} {19421, 19423, 19427, 19429} {21011, 21013, 21017, 21019} {22271, 22273, 22277, 22279} {25301, 25303, 25307, 25309} {31721, 31723, 31727, 31729} {34841, 34843, 34847, 34849} {43781, 43783, 43787, 43789} {51341, 51343, 51347, 51349} {55331, 55333, 55337, 55339} {62981, 62983, 62987, 62989} {67211, 67213, 67217, 67219} {69491, 69493, 69497, 69499} {72221, 72223, 72227, 72229} {77261, 77263, 77267, 77269} {79691, 79693, 79697, 79699} {81041, 81043, 81047, 81049} {82721, 82723, 82727, 82729} {88811, 88813, 88817, 88819} {97841, 97843, 97847, 97849} {99131,
99133, 99137, 99139} {101111, 101113, 101117, 101119} |
|
![]()
|
Suite |
|
|
Voir |
|
|
Aussi |
|
|
DicoNombre |
|
|
Sites |
|
|
Cette page |
![]()