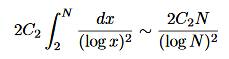NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 31/10/2022 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Nombres PREMIERS
Débutants Nombres Premiers	Constellations				Glossaire Nombres Premiers
INDEX Premiers Types de premiers	Jumeaux	Cousins	Sexy …	Conj. de Polignac
	Records	Triplets, quadruplets	Quintuplets	Sextuplets
	Écarts	Conjecture des premiers jumeaux
		Sommaire de cette page >>> Jumeaux >>> Au départ >>> Liste >>> Premiers jumeaux et somme des chiffres >>> Propriétés >>> Somme des inverses – Constante de Brun >>> Propriétés (suite) >>> Pentium >>> Situation en 2014

Nombres PREMIERS JUMEAUX

Les nombres premiers les plus proches diffèrent de deux unités. On les nomme: nombres premiers jumeaux.

Sont-ils nombreux ? On conjecture qu'ils sont une infinité.

Il y en 16 parmi les 50 premiers nombres premiers.

Le plus grand couple en 2002

318032361 x 2¹⁰⁷⁰⁰¹ + 1 & idem –1

32 220 chiffres

David Underbakke and Phil Carmody

Records

Pour une introduction ludique voir barre magique des nombres premiers

Monsieur et madame veulent divorcer. Ils attendent l'arrivée du deuxième enfant pour se séparer équitablement. Arrivent des jumeaux! Bien embarrassés!

Félicitations, tu as eu des jumeaux. Filles ou garçons?

Je ne sais plus très bien: un garçon et une fille, je crois;

à moins que ce ne soit le contraire.

Gérard et Gilbert sont frères. Ils sont nés le même jour sans être jumeaux. Est-ce possible? Oui! Ils ont un troisième frère. Ils sont triplés.

La blonde accouche de jumeaux. Elle pleure. Pourquoi? Elle se lamente car elle ne sait pas qui est le père du deuxième.

Voir Pensées & humour

NOMBRES PREMIERS JUMEAUX

Définition et commentaires Les nombres premiers jumeaux sont deux nombres premiers dont la différence est égale à 2. Un seul nombre composé les séparent. Normal, un nombre sur deux est pair, donc composé. Mis à part les nombres 2 et 3, il est impossible de trouver deux nombres premiers ne différant que d'une unité. Conjecture des nombres premiers jumeaux: ils sont en quantité infinie. La somme de deux nombres jumeaux est divisible par 12 (situés de part et d'autre de la barre magique des premiers, l'un vaut 6k+1 et l'autre 6k-1, et la somme vaut 12k).

Au départ de la série des jumeaux
Seul 2 et 3 sont séparés d'une unité. Le chiffre 5, comme le 3, est cité deux fois en tant que jumeaux. Tous les jumeaux suivants sont terminés par 1, 3, 7 ou 9	Les quatre nombres premiers 2 3 3 5 5 7 Jumeaux > 5, terminés par 1, 3 7, 9 9, 1

LISTE des premiers jumeaux jusqu'à 1 100
3 5 5 7 11 13 17 19 29 31 41 43 59 61 71 73 101 103 107 109 137 139 149 151 179 181 191 193 197 199 227 229 239 241 269 271 281 283 311 313 347 349 419 421 431 433 461 463 521 523 569 571 599 601 617 619 641 643 659 661	809 811 821 823 827 829 857 859 881 883 1019 1021 1031 1033 1049 1051 1061 1063 1091 1093 De 99 000 à 100 000 99131 99133 99137 99139 99257 99259 99347 99349 99527 99529 99707 99709 99719 99721 99989 99991 De 100 000 à 101 000 100151 100153 100361 100363 100391 100393 100517 100519 100547 100549 100799 100801

Voir Liste de20 000 premiers jumeaux

Nombres sommes de premiers jumeaux

Tous les nombres sauf ceux de cette liste sont somme de paires de premiers jumeaux:

2, 4, 94, 96, 98, 400, 402, 404, 514, 516, 518, 784, 786, 788, 904, 906, 908, 1114, 1116, 1118, 1144, 1146, 1148, 1264, 1266, 1268, 1354, 1356, 1358, 3244, 3246, 3248, 4204, 4206, 4208. OEIS A007534

Prouver que cette liste est finie prouverait la conjecture des nombres premiers.

Premiers jumeaux et somme des chiffres

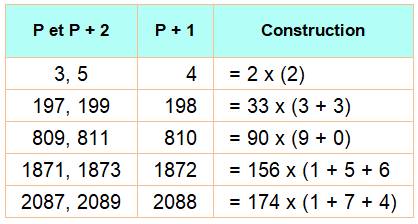
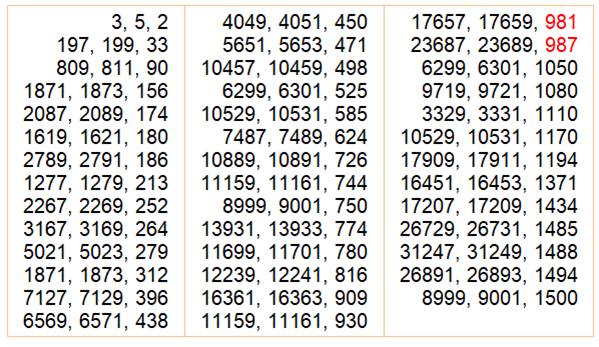
SOMME 63 + (6 + 3) – 1 et 63 + (6 + 3) + 1 sont premiers jumeaux. 864 + (8 + 6 + 4) – 1 et 864 + (8 + 6 + 4) + 1 Ils sont deux jusqu'à au moins un million, plus quatre triviaux: 2 + 2 – 1 et 2 + 2 + 1 / 3 + 3 – 1 et 3 + 3 + 1 6 + 6 – 1 et 6 + 6 + 1 / 9 + 9 – 1 et 9 + 9 + 1 PRODUIT 33 x (3+3) – 1 et 33 x (3+3) + 1 sont premiers jumeaux. Ils sont très nombreux de cette forme. Les cinq plus petits Les suivants (les jumeaux suivis du nombre générateur) Remarquez que 987 est un nombre formé de trois chiffres consécutifs. Seul cas pour n jusqu'à au moins 1 000 000.

Propriétés

Quantité

Quantité de couples de premiers jumeaux jusqu'à n:

n	Quantité	n	Quantité
10	2	10^5	1 224
100	8	10^6	8 169
1 000	35	10^7	58 980
10 000	205	10^8	440 312
100 000	1 224	10^9	3 424 506

Suite en OEIS A007508

Conjecture des nombres premiers jumeaux
Toutes les vérifications possibles laissent penser que les nombres premiers jumeaux sont en nombre infini, mais cela n'est pas démontré.

Simples et jumeaux

Certains cherchent à savoir combien de nombres premiers (en bleu) se trouvent entre chaque paire de jumeaux (en rouge):

2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97 101 103

Kelly et Pilling ont montré que la quantité de premiers simples (en bleu) vérifie une loi logarithmique pour les grands nombres.

Voir développements >>>

Somme de deux jumeaux

La somme de deux premiers jumeaux est

un multiple de douze pour p > 3.

Nombres pairs

Conjecture: sauf pour un nombre fini d'exceptions, les nombres pairs sont la somme de deux nombres parmi les premiers jumeaux.

Exemples: 6 = 3 + 3; 8 = 3 + 5; 10 = 3 + 7; 12 = 5 + 7 …

Exceptions: 2, 4, 94, 96, 98, 400, 402, 404, 514, 516, 518, 784, 786, 788, 904, 906, 908, 1114, 1116, 1118, 1144, 1146, 1148, 1264, 1266, 1268, 1354, 1356, 1358, 3244, 3246, 3248, 4204, 4206, 4208 …

Référence Sloane

Somme des inverses – Constante de Brun

La somme des inverses des nombres premiers jumeaux converge vers

1, 902 …, valeur dite somme de Brun.

1/3 + 1/5 + 1/5 + 1/7 + 1/11 + 1/13

+ 1/17 + 1/19 + 1/29 + 1/31 + ...

= 1,902 160 578 ...

= 1,902 160 583 104 …

La valeur trouvée dépend du nombre de jumeaux pris en compte pour le calcul

Propriété découverte en 1919 par Viggo Brun (1885–1978) et prouvée par lui.

Cette constante a été calculée jusqu'à 10¹⁵

Notez bien que, par contre, la somme des inverses des nombres premiers diverge.

Si la somme des inverses des nombres jumeaux avait divergé, nous aurions eu la preuve qu'ils sont en nombre infini. Manqué!

Anglais: Brun's constant for twin primes

PROPRIÉTÉS (suite)

Caractérisation des jumeaux

Un nombre premier est toujours de la forme 6k – 1 ou 6k + 1. Pour obtenir une différence de deux seulement, le plus petit des jumeaux est en 6n – 1 et l'autre en 6n + 1.

Leur somme est en (6n – 1) + (6n + 1) = 12n, un multiple de douze.

Au-delà de 3

P = 6k – 1

P' = 6k + 1

11 12 13

17 18 19

29 30 31

41 42 43

59 60 61

71 72 73

Formule pour des jumeaux

Si n-1 et n+1 sont premiers jumeaux et n > 5, alors:

n = 30.k + 12.t

avec t un opérateur qui vaut 0, 1 ou -1 et k un entier.

Note: tous les nombres de cette forme n'engendrent pas des jumeaux.
Ex: 48 = 2 x30 – 12 et 49 est composé.

Exemples

p	q	k	t
11	13	0	1
17	19	1	-1
29	31	1	0
41	43	1	1
59	61	2	0
71	73	2	1
101	103	3	1
107	109	4	-1
137	139	4	-1
149	151	5	0
179	181	6	0
191	193	6	1
197	199	7	-1
227	229	8	-1

Valeur de t

Pour p/q de 11/13 à 3581, 3583 (95 jumeaux).

Aucune régularité !

1, -1, 0, 1, 0, 1, 1, -1, -1, 0, 0, 1, -1, -1, 0, 0, 1, 1, -1, 0, 1, 1, 1, 0, 0, -1, 1, 0, 0, 1, -1, -1, 1, 0, 1, 0, 1, 1, 1, 0, -1, 0, 1, 0, -1, 1, 1, -1, -1, 0, -1, -1, 1, -1, 1, -1, 1, 0, -1, -1, 1, -1, 1, 0, 1, -1, -1, 0, 0, 1, 0, 1, -1, -1, 1, 0, 0, 1, 0, 0, 0, -1, 1, -1, 0, 0, 0, 1, 0, 1, -1, -1, 0, -1, 1, …

Quantité de jumeaux

On connaît une formule donnant le nombre estimé de jumeaux.

Formule asymptotique

Quantité de jumeaux jusqu'à N:

C₂ ≈ 0,6601618

Voir Développments

Exemple

< N	Quantité de jumeaux	Estimation
10^6	8 169	6 917
10^8	440 312	389 107
10^10	27 412 679	24 902 847
10^12	1 870 585 220	1 729 364 408
10^15	1 177 209 242 304	1 106 793 221 167

Voir Tableau complet – Wolfram MathWorld et sur OEIS A007508

Cas du PENTIUM

C'est en calculant la constante de Brun pour les nombres jumeaux 824 633 702 441 et 824 633 702 443 que Thomas Nicely a découvert que les calculs faits avec le Pentium étaient erronés. Exemple de calcul faux avec Pentium 4 195 835 - (4 195 835 / 3 145 727) 3 145 727 = 256 au lieu de 0 Intel connaissait ce vice caché et avait minimisé son impact. L'erreur a été corrigée et la puce Pentium remplacée. Source image: Intel et l'erreur de calcul à 500 millions de dollars – Korii – 116/09/220

Deux mecs accoudés au bar se regardent longuement et finissent par s'adresser la parole. – Tu viens d'où toi? – Moi de Melun, et toi? – Quelle coïncidence, moi aussi. Et ils se serrent la main en signe de nouvelle fraternité. – Tu n'as pas l'air d'être très âgé, tu es né en quelle année? – En 1975. – Extraordinaire, moi aussi; et quel mois? – En octobre, le 14 très exactement. – Quoi! Mais c'est inouï, moi c'est le même jour aussi. Et la conversation se poursuit toujours de plus en plus enjouée en constatant autant de points communs.

Alors la porte du bar s'ouvre et Marcel, un habitué, entre dans le bar. Il demande au patron: - Mais qui sont ces deux là? – Oh, c'est rien, ce sont les jumeaux, ils sont encore bourrés.

Voir Pensées & humour

Point de situation en 2014
Pour démontrer la conjecture des nombres premiers jumeaux, il faut prouver qu'il existe une infinité de premiers avec un écart de 2. En 2014, on atteint 246 En admettant la conjecture d'Elliott-Halberstam, l'écart est descendu à 12 voire 6. James Maynard and Terence Tao.

Voir Historique complet et suite: vers la démonstration de la conjecture

Voir Unités des nombres premiers / Les quatre problèmes de Landau

Voir	Records jumeaux Constellation de premiers Types de nombres premiers – Index Nombres premiers – Index Les jumeaux humains Les jumeaux de Langevin Les jumeaux véridiques et menteurs
Aussi	Liste de nombres premiers Décomposition des nombres Nom des nombres Nombres à motifs Nombres composés Représentation des nombres
Diconombre	Nombre 1,902 … – Constante de Brun Nombre 5 Nombre 12
Sites	Nombres premiers jumeaux – Wikipédia Introduction to twin primes and Brun's constant computation - Xavier Gourdon, Pascal Sebah La page des nombres premiers de Chris Caldwell Bug de la division du Pentium – Wikipédia Prime Twins by Ivars Peterson An amazing prime heuristic – Chris K Caldwell Irregularities in the Distribution of Primes and Twin Primes – Richard P. Brent
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Premier/jumeaux.htm