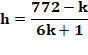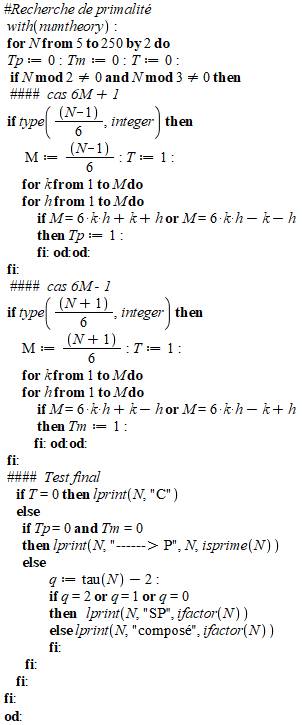|
||||||||||||||||||||||||||||||||||||||||
![]()
|
Nombres premiers P = 6k
|
Voir Résumé
des formes générales des premiers
|
|
||
|
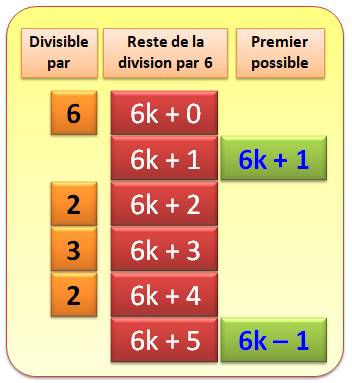
Les
multiples de 6 sont évidemment divisibles par 6. Entre deux multiples de 6
(disons de 6 à 12), il y a cinq nombres qui, divisés par 6, donnent les
restes successifs: r = {1, 2, 3, 4 et 5}.
Et, il n'y en a pas d'autres. On écrit
ces nombres N = 6k + r. Les deux
seuls cas pour lesquels N est susceptible d'être premier sont: Soit
d'une manière générique: |
|
|
|
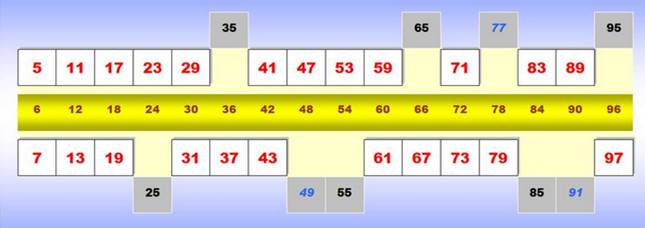
Barre magique des premiers: tous
les nombres premiers sont voisins d'un multiple de 6 (sauf 2 et 3; notez 2 x3 = 6)
Voir Barre
magique des nombres premiers |
||
|
|
||||||||||
Voir
Cercles en 6 |
Condition nécessaire,
mais pas suffisante
|
|||||||||
|
Carré des premiers Tous les premiers au carré (P |
P² = 24k + 1 7² = 49 =
2 x 24 + 1 11² = 121
= 5 x 24 + 1 Voir Divisibilité par 24 |
|||||||||
|
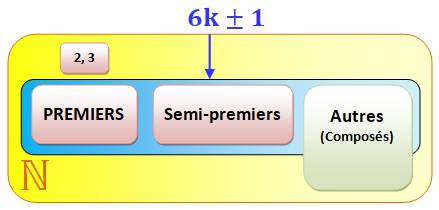
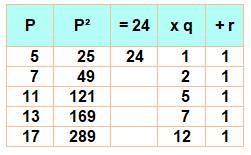
Un nombre semi-premier
est un nombre composé ayant deux facteurs premiers. Chaque facteur est alors
en 6k (6k + 1)(6h + 1) = 36kh + 6k + 6h + 1 (6k + 1)(6h – 1) = 36kh – 6k + 6h – 1 (6k
– 1)(6h – 1) = 36kh – 6k – 6h + 1 Tous de la
forme 6k Voir Explications |
|||||||||
|
Famille des voisins de
6k Tous les nombres premiers et les
nombres semi-premiers appartiennent à cette famille; mais ils ne sont pas les
seuls. La famille comporte des nombres
composés à plus de deux diviseurs propres. Le plus petit est: |
|
|||||||||
|
Premier en (6k – 1):
5, 11, 17, 23, 29, 41, 47, 53, 59, 71, 83, 89 Voir Suite tableau Premier en (6k + 1): 7, 13, 19, 31,
37, 43, 61, 67, 73, 79, 97 Voir Suite tableau Semi-premiers en (6k Cas des nombres en (6k |
|
|
|||
|
Dans la
famille des voisins de 6k, les nombres sont:
Lien semi-premier |
Un nombre composé de la famille est lui-même composé de facteurs de la
même famille. Avec deux facteurs: N = 6M + 1 = (6k + 1)(6h + 1) => M = 6kh + k + h (même raisonnement en introduisant les signes négatifs). Avec trois facteurs: N = 6Q + 1 = (6k + 1)(6h + 1) (6n + 1) Etc. Quelle que soit la quantité de facteurs. |
||
|
Pour N > 3 Réf. History of the Theory of Numbers, Volume
I: Divisibility and Primality – Leonard Eugene Dickson – Page 426 |
Si donc pour un membre de cette famille, il est possible de trouver
des valeurs de k et h, alors le nombre est composé, sinon il est premier. Exemples 175 = 6 x 29 + 1 = 6 (6 x 1 x 4 + 1 + 4) =
6 (6 x 1 x 6 –
1 – 4) 175 = 5 x 5 x 7 => Composé, non semi-premier. |
||
|
Comment calculer k et
h? Prenons N
= 4 633 |
6kh + k + h = 772
Un passage au tableur en plus et en moins pour k, donne: k= - 7 et h =
-19 4 633 = (6x7 – 1) (6x19 – 1) = 41 x 113 Nombre qui est semi-premier. |
||
Merci à H.S. BASTOINI pour tous ses travaux
sur cette propriété
Merci à François L. pour sa relecture attentive
|
|
||
|
…
|
Commentaires Appel du logiciel de théorie des nombres. Boucle de test des nombres de 5 à 250 en excluant
les nombres pairs. Préparation de trois indicateurs. Exclusion des nombres pairs et divisibles par 3. Premier test si le nombre est en 6M + 1. Si oui T prend la valeur 1, témoin du
passage dans cette boucle. Deux boucles en k et h pour chercher pour quelles
valeurs éventuelles on retrouve l'une de nos deux égalités. Si trouvé, on en
témoigne en mettant l'indicateur Tp à 1. Deuxième test si le nombre est en 6M – 1. Si oui T prend la valeur 1, témoin du
passage dans cette boucle. Deux boucles en k et h pour chercher pour quelles
valeurs éventuelles on retrouve l'une de nos deux égalités. Si trouvé, on en
témoigne en mettant l'indicateur Tm à 1. Si T =
0, le nombre n'est pas en 6k Sinon T = 1. Si Tp et Tm sont à 0, c'est qu'une des égalités
n'a été satisfaites et le nombre est premier. Sinon, le nombre est semi-premier ou composé. On reconnait les semi-premiers en comptant les
diviseurs propres (q = 2, 1 ou 0) en tenant compte des carrés. Affichage Les multiples de 2 et de 3 ne sont pas présents. Les nombres premiers sont mis en évidence avec le
mot "true" (vrai) qui ressort à droite. Les semi-premiers (hors ceux avec les facteurs 2
et 3) sont listés avec leurs deux facteurs. On montre le nombre 175 qui le plus petit nombre
de la famille des voisins de 6k et qui n'est ni premier, ni semi-premier. Bilan Cette liste ne constitue en rien une preuve du
théorème, mais une vérification pour les premières valeurs de N. |
|
Voir Programmation – Index
|
|
||
|
Or le nombre et sa racine numérique ont les mêmes
propriétés de divisibilité. La racine numérique d'un nombre premier supérieur
à 3 n'est jamais 0, 3, 6 ou 9. |
Propriété des premiers P = 6k Divisibilité par 3 ? P mod 3
= (6k
= 6k mod 3
= 0 Racine numérique Rn(P) = Rn(P) Rn(P) |
|
Voir Somme des
chiffres et multiples de 6
|
|
||
|
Si un
nombre premier est de la forme 3k + 1, alors il est de la forme 6k + 1. Ex: 31 = 3 x 10 + 1 = 6 x 5 + 1 |
Tous les nombres premiers sont en 6K + 1 ou 6K – 1 que l'on peu écrire: Seule possibilité pour 3k + 1 => 6K + 1 |
|
|
Tout
nombre positif composé de la forme 4k + 3 doit avoir un facteur en 4k + 3. Ex: 143 = 35 x 4 + 3 143 =
11 x 13 et 11 = 4 x 2 + 3 |
Le nombre en 4k + 1 est impair. Donc pas de facteur en 4k ou 4k + 2. Reste 4k + 1 et 4k + 3. Le nombre est composé et comporte au moins deux facteurs Si l'autre est unique et en 4h + 1, avec le premier facteur en 4k + 1
, le produit (4k + 1)(4h + 1) = 4(kh+k+h)
+ 1 serait encore en 4K + 1 et non 4K + 1 Donc, l'autre facteur doit être en 4k + 3. |
|
|
Tout
nombre positif composé de la forme 6k + 5 doit avoir un facteur en 6k + 5. Notez que
les nombres en 6k + 5 sont souvent premiers. Ex: 161 = 26 x 6 + 5 161 = 7 x
23 et 23 = 6 x 3 + 5 |
Un nombre en 6k + 5 est impair et aucun facteur ne peut être en 6k, 6k
+ 2, 6k + 3 ou 6k + 4. Donc, tous les facteurs en 6k + 1 ou 6k + 5. S'il n'y a avait que des 6k + 1, le nombre serait en 6k + 1. Alors, un
des facteurs est nécessairement en 6k + 5. |
|
|
Le carré
d'un nombre premier (>4) moins 1 est divisible par 24. Exemples
Voir Divisibilité par 24 Anglais: if p
is a prime number greater than or equal to 5, then there exists an integer k
such that p = sqrt (24k + 1).This is equivalent to proving: if p is a prime >= 5, then p^2 = 1 mod
24. |
Il faut démontrer:
Si P = 6k + 1 Alors en mod 24
Même type de calcul pour 6k – 1 Dans tous les cas le reste est égal à 1. |
|
|
|
|||
|
Chaque nombre premier peut être en 6k – 1 ou 6k +
1, soit quatre cas pour la différence. La différence entre deux nombres premiers (> 5) est toujours en {6H
– 2, 6H, 6H + 2}. |
Écart entre nombres premiers
|
||
|
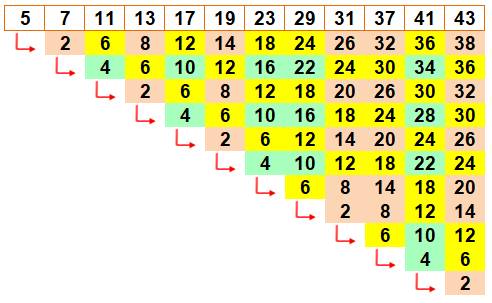
Exemples Chaque ligne indique la différence avec le nombre
dont est issue la flèche rouge. Jaune: écart en 6H; Ocre: écart en 6H + 2; et Vert: écart en 6H + 4 ou 6H' – 2. |
Écart entre les nombres premiers de
5 à 43
|
||
Voir Somme des
chiffres et multiples de 6
![]()
|
Voir |
|
|
Aussi |
|
|
|
|
|
Cette page |
![]()