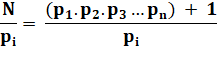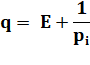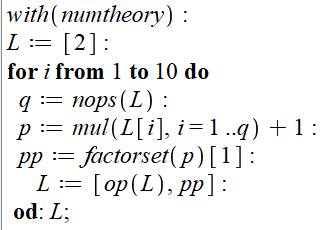NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 07/01/2021 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Nombres PREMIERS
Débutants Nombres Premiers	PROPRIÉTÉS				Glossaire Nombres Premiers
INDEX Nombres premiers	Propriétés	Infinité	Un	Curiosités
	Théorème des nombres premiers		Progressions arithmétiques
	Terminale Spé	Sommaire de cette page >>> Approche >>> Démonstration avec congruences >>> Démonstrations >>> Démonstration la plus courte >>> Primorielles >>> Suite d'Euclide-Mullin >>> Nombres d'Euclide

Infinité de

NOMBRES PREMIERS

Démonstration d'Euclide.

Hyper simple!

Merveilleux!

Il existe une infinité de nombres premiers Euclide – Les Éléments

En notation moderne, la démonstration tient en quatre caractères n! + 1

Il est évident que cette affirmation "il y a une infinité de nombres premiers"

ne pourra jamais être vérifiée complètement.

Par contre, elle peut être démontrée. Et très simplement.

APPROCHE – Principe de la démo
Démontrer qu'il existe un premier plus grand que tout nombre premier donné n.	Exemple n = 7
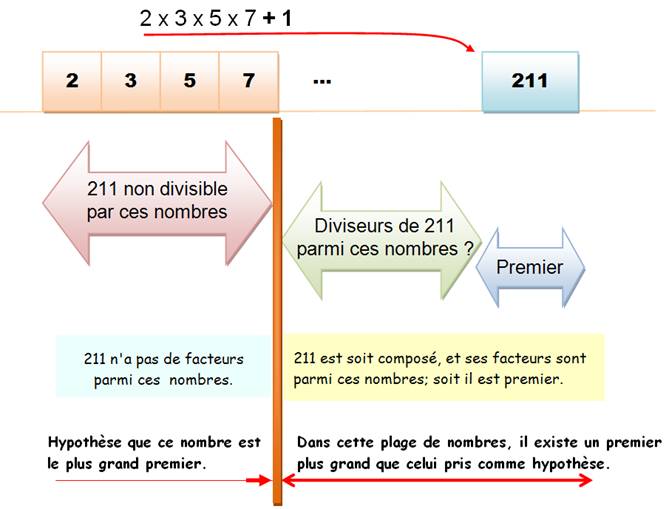
On prend tous les premiers inférieurs, et on ajoute 1.	2 x 3 x 5 x 7 + 1 = 211
Ce nombre divisé par tous les nombres premiers inférieurs à 7 donne 1, par construction.	Exemple 211 = (2 x 3 x 7) x 5 + 1 211 / 5 = 42 x 5 + 1
Ce nombre est donc premier par rapport à tous les premiers inférieurs à 7. En outre, deux seuls cas se présentent: soit, il est premier lui même, soit, il est le produit d'autres nombres premiers plus grands que 7.	En fait, 211 est premier
Ce raisonnement peut être appliqué à tous les nombres premiers connus.	p quelconque 2 x 3 x 5 x 7 x … x p + 1
Notez que ce nombre est composé => Il ne faudrait pas penser que ce type de produit de premiers + 1 est automatiquement premier.	2x3x5x7x11x13 + 1 = 30 031 = 59 x 509

ILLUSTRATION
On fait l'hypothèse que 7 est le plus grand nombre premier. Il suffit de remplacer le nombre 7 par n'importe quel nombre premier, le plus grand que l'on puise imaginer, et mener le même raisonnement pour conclure qu'il y aura toujours un nombre premier encore plus grand.

EUCLIDE – Son raisonnement

Comme montré ci-dessus, Euclide a utilisé le simple nombre un pour démontrer qu'il existe une infinité de nombres premiers. Soit trois nombres premiers A, B et C. On forme le nouveau nombre D = A . B . C + 1 Est-ce que ce nombre est premier? Si oui, alors il existe un nombre premier D supérieur à A, B, C. Si non, alors il a un diviseur premier E qui ne peut être ni A, ni B, ni C. Il existe donc un autre premier E. Que ce soit l'un ou l'autre cas, il existe un nombre premier de plus qu'au départ.

DÉMONSTRATION
On suppose donc que les nombres premiers sont en quantité finie.	p1, p2, p3 … pn-1, pn => n premiers
On forme un nouveau nombre : le produit de tous les nombres premiers auquel on ajoute 1.	N = (p1 . p2 . p3 … pn ) + 1
Deux cas se présentent:	N est premier ou non ?
1) Si N est premier, il y a n + 1 premiers. Un de plus que ce que dit l'hypothèse. Pas possible!	p1 . p2 . p3 … pn & N => n + 1 premiers
2) Si N n'est pas premier, il est divisible par un nombre premier q.	N = A . q
Or, on sait que N n'est divisible par aucun des nombres premiers de la liste initiale. En effet, le reste de la division sera toujours 1. (Quelque soit i, N = 1 mod pi)	q n'est pas parmi p1 . p2 . p3 … pn
Avec q, il y a n + 1 premiers. Un de plus que ce que dit l'hypothèse. Pas possible!	p1 . p2 . p3 … pn & q => n + 1 premiers
Contradiction	Hypothèse fausse : Les nombres premiers ne sont pas en nombre fini, mais infini.

Remarque

La démonstration ci-dessus est la plus rapide, la plus élégante. Celle qui suit est une alternative qui nécessite la connaissance du théorème de la factorisation unique.

Merci à David K. qui a contribué à la précision de cette page.

DÉMONSTRATION – Raisonnement par l’absurde >>>
On suppose l’affirmation fausse: il existe un nombre premier le plus grand: pn. On démontre que cela aboutit à une contradiction.
On suppose donc que les nombres premiers sont en quantité finie.	p1, p2, p3 … pn-1, pn
On forme un nouveau nombre : le produit de tous les nombres premiers auquel on ajoute 1. Ce nombre N est plus grand que le plus grand premier Pn. De ce fait et en conséquence de notre hypothèse, N est composé.	N = (p1 . p2 . p3 … pn ) + 1
N est composé: il admet une factorisation unique, produit de nombres premiers. Ces nombres premiers sont ceux de la liste des premiers de p1 à pn. Soit pi l'un des diviseurs premiers de N.	N = q . pi
Remarque Pi est différent de 1, puisqu'il s'agit d'un nombre premier (un n'est pas premier). De même pour q qui est le produit d'un certain nombre de nombres premiers.
On peut effectuer la division du produit plus un
Le premier terme se simplifie, car pi est dans le produit; on baptise E cet entier.
Or q et E sont deux entiers, donc	1 / pi doit être un entier
On se souvient que pi est supérieur à un.	1 / pi n’est pas un entier
Contradiction!	Hypothèse fausse : Les nombres premiers ne sont pas en nombre fini, mais infini.

EN BREF
On peut résumer ainsi : S’il y avait un nombre fini de nombres premiers, leur produit additionné de 1 serait divisible par l’un deux, donc 1 le serait aussi, ce qui est absurde. Jean Paul Delahaye – Merveilleux nombres premiers

Démonstration courte (la plus courte)
Ce nombre n'est divisible par aucun entier d inférieur ou égal à n (sauf 1). Ses facteurs premiers excédent n. Il existe un nombre premier plus grand que n.	n! + 1 Il existe un premier plus grand que n quel que soit n.

Primorielles
Primorielle (n) = Produit des nombres premiers inférieurs ou égaux à n. Pn = p1 . p2 . p3 … pn est appelé primorielle n P11 = 2 x 3 x 5 x 7 x 11 = 2 310 Les primorielles comme les nombres premiers sont en nombre infini. Voir Démonstration de l'infinitude des premiers avec les primorielles

Nombres premiers jumeaux
Deux nombres premiers dont la différence est égale à 2 sont jumeaux. Sont-ils une infinité ? Nul ne le sait. On conjecture que c'est le cas.

Suite d'Euclide-Mullin
Création La démonstration d'Euclide fait intervenir un nombre spécial: produit des premiers connus +1. Génération d'une suite de nombres premiers du type P = p1.p2.p3… + 1 Avec le nouvel entrant pi qui vaut P s'il est premier ou alors son plus petit facteur premier.	Exemples P1 = 2 P2 = 2 + 1 = 3 P3 = 2.3 + 1 = 7 P4 = 2.3.7 + 1 = 43 P5 = 2.3.7.43 + 1 = 1 801 = 13 x 139 P6 = 2.3.7.43.13 + 1 = 53 x 443 P7 = 2.3.7.43.13.53 + 1 = …
Programme	Commentaires Appel au logiciel de théorie des nombres. La liste des nombres premiers L est initialisée avec 2. Lancement d'une boucle pour dix fois le même calcul. La quantité de nombres premiers déjà trouvée est en q. Le nombre d'Euclide p est calculé en multipliant tous les premiers de la liste L plus 1 . Le nouveau nombre premier pp est le plus petit des facteurs de p. C'est celui qui est en première position [1] de la liste des facteurs de p (factorset). On ajoute ce nombre pp à la liste des premiers. Après la fin de boucle (od), on demande que la lite L soit affichée.
Propriétés Les nombres premiers trouvés ne sont pas répétitifs. En 1963 Mullin se demande si cette construction finit par donner tous les nombres premiers. En 1991, Daniel Shanks conjecture que non. La difficulté est que les nombres deviennent vite très grands. Avec 43 nombres premiers, la factorisation a été obtenue en 2010 par Wilfrid Keller. Avec 52, la factorisation date de 2012 par Ryan Propper. Avec le programme proposé, mon ordinateur met plusieurs heures pour calculer les 30 premiers.		Liste des 51 connus par groupe de 10 En rouge les plus petits premiers jusqu’à 37 (la position du nombre 41 est inconnue) 2, 3, 7, 43, 13, 53, 5, 6221671, 38709183810571, 139, 2801, 11, 17, 5471, 52662739, 23003, 30693651606209, 37, 1741, 1313797957, 887, 71, 7127, 109, 23, 97, 159227, 643679794963466223081509857, 103, 1079990819, 9539, 3143065813, 29, 3847, 89, 19, 577, 223, 139703, 457, 9649, 61, 4357, 87991098 7225522727 0828125179 3312351581 0993928517 6889374801 2603709343, 107, 127, 3313, 22743 2689108589 5327549849 1507577484 8386671439 5682604207 5441494078 0761245893, 59, 31, 211 …
Nombres d'Euclide Nombre primoriels plus 1: produit de tous les premiers nombres premiers plus un. On ne sait pas s'il en existe une infinité composé, comme premiers.			Exemples P1 = 2 P2 = 2 + 1 = 3 P3 = 2.3 + 1 = 7 P4 = 2.3.5 + 1 = 31 P5 = 2.3.5.7 + 1 = 211 P6 = 2.3.5.7.11 + 1 = 2311 P7 = 2.3.5.7.11.13 + 1 = 30 031 = 59 x 509

Voir Programmation – Index / Types de nombres premiers

Suite	Propriétés des nombres premiers Conjecture des nombres premiers jumeaux Progressions arithmétiques
Voir	Euclide Infini Modulo & Congruences Nombres Premiers Primalité Pseudo Premiers Quantité de nombres premiers
Diconombre	Nombre UN
Sites	Euclid-Mullin Sequence – Wikipedia OEIS A000945 – Euclid-Mullin sequence OEIS A056756 - Where n-th prime appears in Euclid-Mullin sequence
Cette page	http://villemin.gerard.free.fr/ThNbDemo/NbPreInf.htm