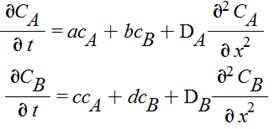|
|||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Phyllotaxie – Développements Interprétation physiologique, chimique Principales
hypothèses expliquant l'arrangement doré des feuilles ou fleurs et approches
mathématiques. Les modèles
physiques ne donnent pas complète satisfaction. Les chercheurs imaginent
l'action de substance biochimiques. Cette page est faite pour tous ceux qui
voudraient toucher du doigt le domaine de la phyllotaxie explicative.
Autrement-dit, il s'agit d'une approche simplifiée (simpliste). Toute erreur
d'interprétation serait de mon fait. |
|
|
||
|
Diffusion d'un inhibiteur |
Hypothèse
d'inhibition de Shoute
(1913). Le méristème apical, et Celle-ci,
en se diffusant, empêche la formation de nouveaux primordia dans la zone
proche où la concentration de l'inhibiteur dépasse un certain seuil. Un
nouveau primordium se développe dès qu'en un point la concentration descend
en dessous du seuil (Illustration de Shoute montrant le principe
de croissance; Shoute sait que la représentation
géométrique n'est pas réaliste). Richards(1951)
et Schwabell (1969). |
|
|
Diffusion-réaction |
Théorie morphogénétique de diffusion-réaction: les substances chimiques en jeu agissent favorisant ou non la
croissance selon leur concentration et leur délai d'action, créant un champ
de gradients morphogénétiques. Turing (1952). |
|
|
Mutilation |
Expérience
de la fougère coupée: une coupure est pratiquée de part et d'autre d'un
primordium. Libéré de l'influence de son voisinage, il se développe plus
vite. Wardlaw (1949). Expérience
contestée par Maksymowych en 1977 sous prétexte de
possibles effets collatéraux dus à la mutilation des cellules. |
|
|
Répulsion chimique |
Rôle de l'auxine dans le développement du méristème et la
production foliaire. Son accumulation est nécessaire pour initier la
formation d’un organe. C. Kuhlemeier (vers 2005). L'auxine
est une hormone végétale,
facteur de croissance, découverte en 1937. C'est un agent reconnu pour
contrôler les réactions des plantes à la lumière, la gravité, à
l'hygrométrie, la nervation des feuilles et … les structures phyllotaxiques. Il aura
fallu attendre la fin du XXe siècle pour que l'auxine soit
reconnue comme à l'origine de la formation des feuilles et des fleurs au
niveau du méristème apical (MAC) |
|
|
Synthèse |
"Explications qui s'inspirent de la
biochimie : les organes (cellules, primordia, feuilles ou fleurs, fibres) ont
une croissance orientée, influencée par les cellules ou les organes
voisin(e)s, par contact direct, selon un "langage" chimique
codé." Selon JPM. Chabert |
|
|
|
||
|
Alan Turing publie
en 1952: The Chemical basis of Morphogenesis. Une
théorie chimique semblable à celle de Schoute
(1913). |
||
|
Théorie morphogénétique de diffusion-réaction: les substances chimiques en
jeu agissent favorisant ou non la croissance selon leur concentration et leur
délai d'action, créant un champ de gradients
morphogénétiques. Ces modèles, pourtant simplifiés à l'extrême, font appel à
des équations
différentielles très difficile à résoudre analytiquement, sauf à se
mettre dans des cas particuliers. |
Exemple: ces deux équations différentielles
prennent en compte la loi de diffusion de Fick, la
production et la dégradation de l'inhibiteur, le transport dans la direction
de l'axe des y. Les concentrations sont représentées par DA et DB.
|
|
|
Résultats: ce modèle
mathématique témoigne bien de l'apparition des structures
spiralées. Turing est le premier à ramener les lois de description des
formes botaniques de croissance
(biologie) aux règles d'évolution des systèmes dynamiques (physique
mathématique). Ce sont des jeux de contraintes qui régissent l'évolution du
mouvement. |
Modéle mathématique et ordinateur: Turing, co-fondateur de l'informatique moderne, est le premier à faire
tourner son modèle sur ordinateur. (À ce titre, il devrait figurer dans le chapitre suivant) Exemples de paramètres pris en
compte:
|
|
|
Avec
la recherche de causes physiologiques, les chercheurs essaient de trouver la raison
profonde d'une phyllotaxie si régulière. La
vision arithmétique comme la vision géométriques se contentaient de constater, de
caractériser. Désormais on tente d'expliquer. En
tout les cas, les chercheurs constatent la complexité des phénomènes et
doivent se résoudre à inventer des modèles
sophistiqués dont les résultats ne pourront être constatés qu'à l'issue
de calculs sur ordinateurs. |
![]()
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/aScience/Botanique/PhylChim.htm
|
![]()