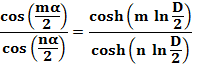|
||||||||||||||||||||||||||||||||||||
![]()
|
Phyllotaxie - Historique Principales étapes de la
recherche en phyllotaxie. Recherche de la modélisation
unificatrice. Cette page décrit les étapes chronologiques. Pour une vison
thématique voir les pages développements. |
![]()
|
1202 Leonardo Fibonacci |
Découvre la suite de Fibonacci en comptant
les lapins qui se reproduisent. Cette suite de nombres, avec ses cousins, le nombre d'or et l'angle d'or,
vont prendre de l'importance en phyllotaxie. |
|
1503 Léonard de Vinci |
Observe
la forme spiralée de la croissance des
plantes. La sixième
feuille est toujours au-dessus de la première, sauf empêchement. Toutes les
branches d'arbres, à quelque degré de hauteur qu'on les réunisse, sont égales
à la grosseur du tronc. Tous les ans, quand les branches des arbres ont
achevé de se développer, leur grosseur – si on les réunit toutes – équivaut à
celle de leur tronc. |
|
1754 Charles Bonnet |
Recherches sur l'usage des feuilles
dans les plantes. Première
étude sérieuse sur l'organisation des
feuilles. Il distingue les quatre types encore utilisés aujourd'hui.
Linné adopte la même classification. Il observe la nature spiralée et émet l'hypothèse que les feuilles ne
se recouvrent que le plus faiblement possible pour permettre la libre
circulation de l'air. |
|
vers 1600 Johannes Kepler |
Fasciné
par la géométrie et par le nombre 5, présent
en botanique et absent en minéralogie, il prétend que la suite de Fibonacci est impliquée ("semée") dans
la croissance des plantes. |
|
1807 Goethe |
Morphologie: Goethe,
le poète allemand, est le fondateur de
la morphologie végétale (il invente ce mot). Il tente de construire une plante idéale qui
serait la base pour en déduire toutes les autres. Il reconnait une tendance
spiralée de la nature. Par contre, il répugne à mathématiser la nature vivante. |
![]()
|
1830 Karl Schimper |
Spirale génétique – Analyse arithmétique: Il introduit la notion de Parastiques.
Il note que ces spirales sont en 1/3, 2/5 et 3/8, des nombres successifs de la suite de Fibonacci. Il définit l'angle de divergence en tant que
fraction et introduit le
nombre d = nombre de cycles autour de la tige, divisé par la quantité de
feuilles par cycle. |
|
1835 Allexander Braun |
Organisation en double spirale: le cône de pin, comme d'autres plantes, sont organisées en deux types
de spirales l'une dextre l'autre senestre; et chacune en quantité comme deux nombres consécutifs de Fibonacci. |
|
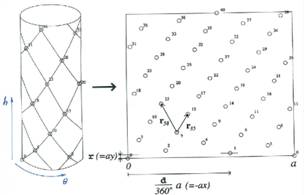
1837 Bravais Louis et Auguste |
Essai sur la Disposition des
Feuilles Curvisériées Réseaux de Bravais – Analyse géométrique: disposition des feuilles sur une
sorte de treillis (maillage ou lattice en anglais) posé sur un cylindre. Notion de spirale génétique et de spirale
secondaire. Exemple: si on compte 6 et 16 spirales, la spirale génétique est
du type 3/8, le PGCD étant 2). Il note que l'angle de divergence est
irrationnel. Le plus courant étant l'angle d'or.
Note: Auguste Bravais est le père de la cristallographie.
|
|
1848 Lestiboudois |
Trouve
une relation entre les formes phyllotaxiques et le
phénomène de ramification des branches. |
|
1868 Wilhelm Hofmeister |
Axiome de Hofmeister – Premières explications mécanistiques: chaque feuille primordiale naît dans le plus
grand espace libre immédiatement disponible entre les deux feuilles
précédentes. Travaux en allemand non traduits, sans suite
durant cinquante ans. Suite >>> |
|
1872 Peter Guthrie Tait |
Affine les
conclusions des frères Bravais. |
|
1873 Airy |
Densité maximale de primordia: Airy s'intéresse à la zone de naissance et énonce un principe d'économie d'espace. Désormais, ses successeurs
vont se focaliser sur cette zone (méristème). |
|
1875 Julius von Wiesner |
Loi de Wiesner: la divergence entre feuilles consécutives est telle qu'elles
optimisent l'exposition
à la lumière tout en facilitant leur transpiration. Loi qui s'inscrit dans
la lignée de la théorie de l'évolution de Darwin
ou encore de la génétique mendélienne. En 1988, Niklas prouve par simulation sur ordinateurs que le besoin de lumière ne conduit pas nécessairement à
l'angle d'or. |
|
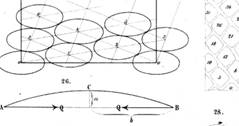
1878 Simon Schwendener |
Champ de tension (contraintes biophysiques) qui naît autour des primordia,
contrôlant la position du nouveau primordium. Base de la théorie reprise par Schuepp en 1966. Modèle analogique: pour convaincre, il réalise des figures géométriques avec règle et |
|
1881 De Candolle |
Explication mathématique des théories de Wiesner et de Airy. Les fractions utilisées non pas de fractions
médianes (fractions obtenues en ajoutant numérateurs entre eux et les dénominateurs
entre eux, donnant naissance à la suite de Farey).
Notion
qui, ici, est relative à la combinaison de parastiques. Pour une valeur
donnée, en réduisant l'espace des entrenœuds, la fraction médiane va entrer
en jeu. Ce serait une manière d'expliquer les transitions entre diverses
formes phyllotaxiques dues à des discontinuités ou
des instabilités. Les études dans ce domaine reprendront seulement à partir
de 1974 avec Adler et d'autres. >>> |
|
1882 Julius Sachs |
Texte de
référence durant plusieurs décennies. Pas de maths en botanique: Sachs considère que les nombres, les fractions, et autre angle d'or
ne sont que des visions arbitraires de la réalité, un jeu mathématique! Ce
fut un frein au développement de la phyllotaxie théorique. |
![]()
|
1904 Church |
Théorie équipotentielle de
la phyllotaxie: fondée sur l'hypothèse de la spirale logarithmique. L'énergie
vitale se comporterait comme l'énergie électrique.
Le spirales seraient les équipotentielles,
des lignes de forec. Les modélisations
contemporaines reprendront ces idées. Représentation centrée: sections perpendiculaires
à l'axe, une représentation, dite polaire,
qui sera adoptée durant la période contemporaine à la place de la
représentation cylindrique. Les deux sont mathématiquement équivalentes. |
|
1907 Van Iterson |
Modèle dense: les primordia se rangent de façon dense
autour d'un cylindre. Modèle identique à celui de la pression de
contact engendré par la croissance. Le
premier à avoir tenté de comprendre leur lien profond avec la suite de Fibonacci. Travaux méconnus jusqu'en 1973 (Erikson). Il étudie les différents agencements de billes
autour d'un cylindre de taille variable. Il dessine un diagramme donnat les configurations possibles selon l'angle de
divergence d et le rayon du cercle D. Son équation, avec alpha, angle de divergence, D
le diamètre des sphères placées autour du cylindre:
Sa résolution nécessite une série
d'approximations successives. Suite >>> |
|
1913 Schoute |
Théorie de la diffusion d'un
inhibiteur ou hypothèse d'inhibition de Shoute: le méristème apical, et chacun des primordia en croissance, produit
une substance chimique inhibitrice. Suite >>> |
|
1917 D'Arcy Thompson |
On Growth and Form (réédité en 1942) Premier
biomathématicien. Il prétend que ses prédécesseurs ont sous-estimé
le rôle de la physique et de la mécanique dans la constitution des formes des
organismes vivants. En phyllotaxie, il retrouve la suite de Fibonacci. Suite >>> |
![]()
|
1920 Lucien Plantefol |
Théorie des hélices foliaires. Succès dans les années 1940 puis abandonnée. En fait, il reproche l'idéalisation géométrique
qui permettrait de faire coller la réalité au modèle. Il trouve aussi qu'il
existe beaucoup trop d'exceptions. Même idée que Sachs (1882). La
réalité biologique réside dans une seule famille de spirales. Théorie spirales parallèles reliant les feuilles
de deux en deux ou de trois en trois, etc., de manière à ce que l'on tombe
toujours sur une spirale définie rigoureusement d'un point de vue
géométrique. Coup de
frein jusque dans les années 1960 à la biologie théorique (en France). |
|
1922 Ronald Fisher |
Loi de Fisher – loi de
probabilité continue: loi générale qui permet en
botanique l'étude des plantes avec les outils de la statistique. Expérimentation par blocs (carrés latins pour établir des
plans d'expérience). Méthode qui permet de prendre en compte de multiples
paramètres et surtout de minimiser les effets aléatoires. L'idée est de découvrir quelles sont les causes
de la croissance végétale et leur poids relatif. |
|
1931 Snow Mary et Robert |
Théorie du premier espace disponible: reprennent la règle d'Hofmeister (1868) de la
première place disponible, et ils ajoutent que: chaque nouvelle feuille doit
naître à une certaine distance minimale sous la pointe de l'apex dans un
espace d'une grandeur minimale déterminée. Une théorie mixte qui s'appuie sur une longue
série de recherches expérimentales et qui conjugue un facteur mécanique
(l'espace disponible) et un facteur d'inhibition. Les époux Snow utilisent la
micro-ablation pour démonter leur thèse. |
|
1937 Frits Went et Kenneth Thimann |
Identification
et caractérisation de l'auxine, la première phytohormone. Un agent reconnu
pour contrôler les réactions des plantes à la lumière, la gravité, à
l'hygrométrie, la nervation des feuilles et … les structures phyllotaxiques. |
|
1948 F.J. Richards |
Il reprend
les travaux de Church, jusqu'alors ignorés. Ratio plastochrone R: rapport entre les distances de deux feuilles successives à partir du
centre du disque et le nombre de parastiques qui se voient le plus. Un système d'équations
modélise la représentation centrée et met en œuvre trois paramètres: le
rapport plastochron, l'angle de divergence et
l'angle du cône tangentiel au sommet de la zone étudiée. |
|
1949 Wardlaw |
Expérience de la fougère coupée: une coupure est pratiquée de part et d'autres d'un primordium. Libéré
de l'influence de son voisinage, il se développe plus vite. Expérience
contestée par Maksymowych en 1977 sous prétexte de
mutilation des cellules. |
|
1951 Richards 1969 Schwabell |
Théorie du champ inhibitif: suite aux travaux de Schoute (1913), cette
théorie est en opposition avec celle de la
pression de contact d'Adler (1974). |
|
1952 Snow |
Conteste
partiellement l'hypothèse de Schoute (1913). Les successeurs
vont la compléter et la modéliser. |
|
1952 |
Turing publie: The Chemical basis of
Morphogenesis Une
théorie chimique semblable à celle de Schoute
(1913) Théorie morphogénétique de diffusion-réaction: les substances chimiques en jeu agissent favorisant ou non la
croissance selon leur concentration et leur délai d'action, créant un champ
de gradients morphogénétiques. Turing est
le premier à faire tourner son modèle sur ordinateur. Suite >>> |
![]()
|
1970 Hisao Honda |
Simulation graphique sur ordinateur de la croissance des formes arborescentes (arbres). Langage
de l'époque le FORTRAN. Collaboration avec un autre Fisher prénommé Jack,
botaniste de terrain. |
|
1974,
1977 Adler |
Théorie de la pression de contact des primordia: chaque feuille croit en diamètre jusqu'à ce quelle touche sa voisine le
plus proche, après quoi elle essaie de grandir. Sa simulation montre les
limites du modèle. Théorème fondamental de la phyllotaxie: il vise à clarifier la confusion due à l'observation d'hélices
multiples. Il donne la relation entre le compte des spirales
observées dans un réseau cylindrique et l'angle horizontal entre les points
successifs verticalement dans le réseau. Suite >>> |
|
1975 Thorney 1977 Veen-Lindenmayer 1978 Young |
Modélisation sur ordinateur: la représentation géométrique de la théorie de la diffusion d'un
inhibiteur (Schoute) est difficile sinon
impossible. Seule, une simulation dynamique peut témoigner de l'action
d'inhibition au fur et à mesure de la naissance des primordia. Ces modèles
aboutissent à des résultats qui confirment ce que crée la nature, témoignant
que les paramètres pris en compte seraient les bons. Veen-Lindenmayer reprend le modèle géométrique de Van Iterson(1907) et introduit le concept de gradient
chimique. Un réel progrès, car ce modèle prend en compte le facteur temps. |
|
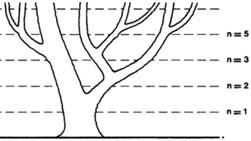
1960 H. Steinhaus |
Loi de croissance fibonacienne: une branche d'arbre ne produit pas de nouvelle banche durant sa
première année de croissance. Ensuite, elle produit une branche une année sur
deux. Le résultat est montré sur l'illustration.
Alors, la
quantité de branches suit la série de Fibonacci: 1, 1, 2, 3, 5, 8, … Nombre
que Fibonacci, lui-même, avait trouvée en comptant
les générations de lapins. |
|
1966 Schuepp |
Reprend Scwendener |
|
1968 Wardlaw |
Reprend
la théorie de Turing et l'illustre sur des cas relativement simple. |
![]()
|
1972 Coxeter |
The Golden Section and Phyllotaxis – 1969 The Role of Intermediate Convergents in Tait's
Explanation for Phyllotaxis – 1972. |
|
1974 Meinhardt |
Reprend Turing |
|
1981 Rutishauser |
Modélisation |
|
1981,
1982 Meicenheimer |
Travaux
sur l'épitélium |
|
1983 Erikson |
Redécouvre
et étend les travaux de van Iterson (1907). |
|
1983 Bilan selon Roger V. Jean |
Quatre types de modèles de phyllotaxie
Pression de contact: Jean reprend la modélisation basée sur cette notion imaginée par
Adler (1973) |
|
1984 Roger Jean |
Reformule
le théorème fondamental de la phyllotaxie et lui en donne une interprétation
intuitive. En fait, publie énormément sur le sujet. En 1987,
résumé du fruit de ses recherches avancées: Après une décennie de modélisations mathématiques
sur le phénomène de formes spiralées rencontrées sur les plantes, la
phyllotaxie, le but de cet exposé est de donner de nouvelles impulsions vers
une solution complète. (…) Des progrès ont été accomplis dans cette
direction en faisant les hypothèses suivantes:
Nous allons montrer que le modèle développé
produit les généralisations annoncées |
|
1985 Rutishauser et Sattler |
Modélisation |
|
1988 Lacroix et Sattler |
Modélisation |
|
1991 Leonid Levitov |
Modèle de la maximalisation de l'énergie de
répulsion: Expérimente un modèle sous contrainte mécaniques
et observe la régularité des nombres de Fibonacci Le modèle est celui
des billes densément réparties autour d'un cylindre avec croissance sous
contraintes (stress) anisotropiques (croissance
axiale lente et radiale rapide comme observée chez les plantes). Levitov (MIT) conclut: this behavior is robust:
Fibonacci phyllotaxis is explained. |
|
1992 puis
1996 Douady et Couder |
Simulation numérique des formes phyllotaxiques sur la base notamment des hypothèses de Hofmeister
(1868). Au lieu de se baser sur des critères géométriques
pour expliquer l'emplacement des primordia nouveaux, ils utilisent la notion
d'énergie minimale. Ce modèle a l'avantage d'être applicable à
d'autres phénomènes qui seraient similaires hors de la botanique. Modèle du fluide magnétique: une goutte de fluide magnétisée est lâchée régulièrement au centre
d'une coupelle, où, se comportant comme des dipôles magnétiques, elles se
repoussent mutuellement en migrant vers le bord de la coupelle. Selon le
rythme de la chute des gouttes, l'angle de divergence oscille pour converger
vers l'angle d'or. |
|
1996 Wagenitz |
|
|
1996 Green, Steele et Rennich |
Démontrent
que le stress physique est tout aussi capable de produire les arrangements phyllotaxiques semblables à ceux engendrés par la
morphogénèse de Turing. |
|
1998 Douady |
Modélisation |
|
2000 Didier Reinhardt et al. |
Rôle de
l'auxine dans la formation des feuilles, mais pas généralement pour la
croissance du méristème. |
|
2002 Atela et al. |
Modélisation |
|
vers 2005 C. Kuhlemeier |
Répulsion chimique: rôle de l'auxine dans le
développement du méristème et la production foliaire. Son accumulation est
nécessaire pour initier la formation d’un organe. |
![]()
Note: Dupont et al. pour
et alii (pluriel se alius)
qui veut dire: et autres personnes.
![]()
|
Suite |
|
|
Voir |
|
|
Site |
|
|
Cette page |
http://villemin.gerard.free.fr/aScience/Botanique/PhylHist.htm
|
![]()