NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 21/09/2022 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	PHYSIQUE
Débutants Général	Élémentaire			Glossaire Général
INDEX SCIENCES	BASES	Levier	Treuil	Support
		Forces	Plan incliné	Poutres
		Sommaire de cette page >>> Balançoire et autres objets courants >>> Principe à la Stevin >>> Loi du levier >>> Exemple >>> Simon Stevin

Donnez-moi un point d'appui, je soulèverai le monde.

ou

Donnez-moi une place où me tenir et je mettrai la Terre en mouvement.

Archimède a démontré la loi du levier. Il a introduit la notion fondamentale de centre de gravité et a déterminé son emplacement pour de nombreuses figures géométriques.

Archimède – Traité des équilibres  des figures planes

Voir Pensées & humour

Balançoire et autres objets courants
On connaît la balançoire des jardins d'enfants. Il faut mettre des enfants de même poids de chaque côté, sinon ça ne marche pas bien. La planche est posée sur un pivot. Pour obtenir l'équilibre, le pivot est au milieu de la planche.
Un pied-de-biche, un arrache-clou (nail-claw), ou un levier pour soulever et déplacer les blocs de pierres; L'outil prend appui sur sa partie coudée. Le manche est actionné pour lever le petit embout placé sous l'objet à lever. Du fait de la taille du manche comparée à celle de l'embout, la force exercée par l'embout sur l'objet est décuplée. C'est un effet de levier.
Un sécateur de branches possède lui aussi de grandes poignées qui permettent d'exercer sur les lames de coupe une pression bien plus grande que celle de vos bras.

Principe à la Stevin
Une poutre homogène en équilibre est suspendue en son milieu (centre de gravité). De sorte que l'on a de chaque côté: Même volume Même masse (même poids)
Voici la même poutre en équilibre, à ceci près qu'elle a été coupée en deux: l'un des morceaux deux fois plus gros que l'autre. Chaque morceau est bien en équilibre, car suspendu en son milieu. L'ensemble est aussi en équilibre car suspendu de la même manière que la poutre entière: la corde et l'anneau sont au même endroit. Le levier (rouge) est là pour assurer la suspension des deux morceaux (on néglige la masse de ces dispositifs: cordes et levier).	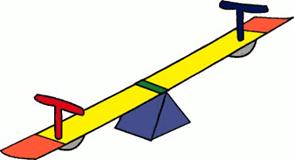On observe que là ou la masse est moitié la longueur du levier est double. Tout le secret du levier est dans cette figure astucieuse!

Loi du levier Deux corps s’équilibrent à des distances inversement proportionnelles à leur poids.
Chaque morceau de poutre a une masse, un poids; en fait chaque morceau exerce une force sur le levier, symbolisée par une flèche (A et B). On laisse de côté la force de résistance C qui doit être suffisante pour supporter l'ensemble des masses. La force A s'exerce sur le bout du bras de levier de longueur a. La force B s'exerce sur le bout du bras de levier de longueur b. L'équilibre est réalisé si la plus grande force s'applique sur le plus petit bras et réciproquement la plus petite force sur le plus grand bras et cela dans les mêmes proportions. Cela correspond au sens commun: la petite force est amplifiée par un grand bras de levier. Une force qui agit au bout d'un bras de levier de longueur a est caractérisée par le produit A.a qui est appelé le moment de la force.	Condition d'équilibre: loi du levier A . a = B . b Les moments des forces (A . a et B . b) sont égaux. Exemple Si A=3 et B=1 alors a=1 et b=3. Si A=1 et B=1 alors a=1 et b=1, cas de la balançoire. Unités La force se mesure en newtons (N). Un newton correspond en gros à un poids de 1/10 de kg. L'unité de moment est le newton-mètre (N-m).

Exemple de calcul
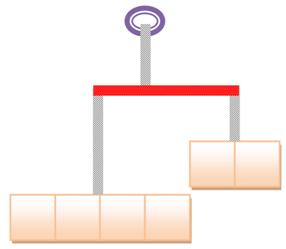
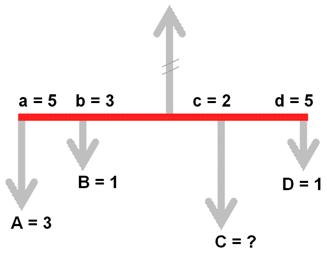
Quelle est la valeur de C pour réaliser l'équilibre ? Écrivons la loi du levier donnant l'égalité des moments d'un côté et de l'autre du point de suspension (ou du pivot). A.a + B.b = C.c + D.d 3x5 + 1x3 = 2C + 1x5 2C = 15 + 3 – 5 = 13 C = 6,5 N

Simon STEVIN (1548-1620)
Mathématicien et ingénieur flamand. Intendant dans l'armée et inspecteur des digues et canaux des Pays-Bas. Précepteur de mathématiques et de sciences pour Maurice de Nassau, prince d'Orange. 1582: De Thiende (le Dixième), premier traité européen connu traitant des notations des nombres décimaux. Heureusement cette notation sera simplifiée. >>> 1586: Les éléments de l'art de peser, ouvrage qui traite de la mécanique statique, de l'équilibre des charges.
L'Arithmétique de Simon Stevin de Bruges – Copie du livre original

Ces pages sont largement inspiré de l'ouvrage indiqué en référence, que je recommande si vous voulez continuer à comprendre la mécanique statique y compris dans l'eau.

Si tous les outils pouvaient, lorsqu'on les commande ou même de leur propre chef, faire le travail qui les incombe […], alors les ouvriers-maîtres n'auraient plus besoin d'apprentis, ni les seigneurs d'esclaves. Aristote

Voir Pensées & humour

Suite	Treuil
Voir	Archimède – Biographie Archimède et ses contemporains Centre de gravité Équations (analogie de la balance) Histoire Euréka Multiplication Sciences – Index
Aussi	Dicomot
Livre	Petite logique des forces; Constructions et machines – Paul Sandori – Points Sciences – 1983 Livre très abordable par tous.
Cette page	http://villemin.gerard.free.fr/aScience/Physique/Levier.htm