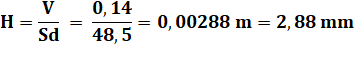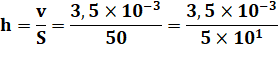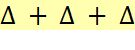|
|||||||||||||||||||||||||||||||||
![]()
|
Principe d'Archimède Un corps plongé dans un
fluide reçoit une force verticale dirigée vers le haut égale et opposée au poids du fluide déplacé. D'accord, mais qu'est-ce que
cela veut dire. Comment visualiser? Comment interpréter? Comment le retenir
une fois pour toute? |
Illustration
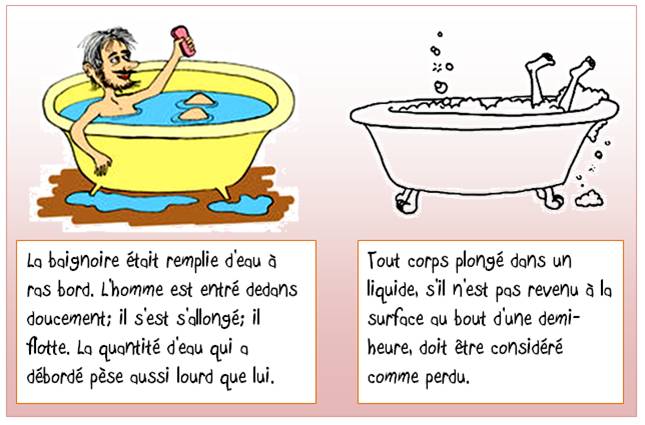
Note: la densité moyenne du corps humain
(1,062 g/cm3) est proche de celle de l'eau.
Dit-autrement: le volume d'un homme de 70 kg est
légèrement supérieur à 70 litres.
Voir Molécules d'eau du
bain d'Archimède
|
|
|||
|
|
|
||
|
Pour le même volume de deux objets |
Densité: rapport entre les deux masses. Masse
volumique: masse de l'objet par unité de volume. |
||
|
Approche, en gros |
Un objet plus dense "s'enfonce" dans le moins
dense. Un objet peu dense "reste en surface" d'un
objet plus dense que lui. |
||
|
Modifier la densité |
Prenons un objet lourd. Plus
il est évidé, gardant le même volume, il devient moins dense. Il devient
"plus léger" (pour un volume donné). Voilà pourquoi les objets creux
comme les bateaux flottent. |
||
Voir Notion
de pression
|
|
|
|
Explication plus précise ci-dessous |
|
|
Principe
d'Archimède appliquée au sous-marin:
À
la conception, la pesée du sous-marin est calculée pilepoil. Durant la navigation,
des réservoirs (ballasts) sont remplis
d'eau ou d'air pour faire descendre ou monter l'engin. En cas de gros
problème, le sous-marin peut remonter en lâchant un lest
embarqué en permanence. |
Voir Sous-marins
|
(ex principe d'Archimède) |
|
|
Approche
Théorème Formulation
brève: poids du volume d'eau. En valeur, la poussée
d'Archimède est égale au poids du volume de
liquide déplacé. Formulation précise: un objet
immergé déplace autant d'eau que nécessaire pour obtenir l'équilibre. Dans un liquide,
plongeons un objet qui va flotter. Cet objet s'enfonce en déplaçant un volume de liquide d'un poids
égal à celui de l'objet entier. Proposition n°V d'Archimède La résultante des
forces de pression exercées sur un corps totalement immergé dans un fluide
est opposée au poids du fluide déplacé. Formulation de la poussée: constat
de l'équilibre. Tout corps plongé
dans un fluide au repos, entièrement mouillé par celui-ci ou traversant sa
surface libre*, subit une force verticale,
dirigée de bas en haut et opposée au poids du volume
de fluide déplacé; cette force est appelée poussée d'Archimède. * Autrement-dit:
flottant ou complètement immergé.
Proposition
VII d'Archimède Le centre de poussée G
|
|
Voir Poussée
d'Archimède dans l'air
|
Pourquoi un glaçon ne fait-il pas déborder le verre en
fondant ? Parce que le volume occupé par la partie immergée (dans
l'eau) est exactement égale au volume d'eau liquide produite après la fonte
du glaçon. Quand le glaçon est dans sa position d'équilibre, le
volume occupé par sa partie immergée correspond exactement au volume d'eau
liquide nécessaire pour égaler le poids total du glaçon.
|
Note: le symbole "égal avec
accent circonflexe" veut dire "correspond à"
Symbole réalisé avec le symbole "angle" mis sur le signe égal.
|
|
||
|
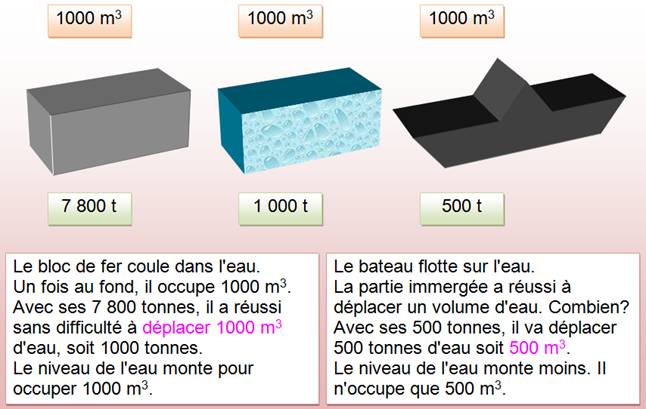
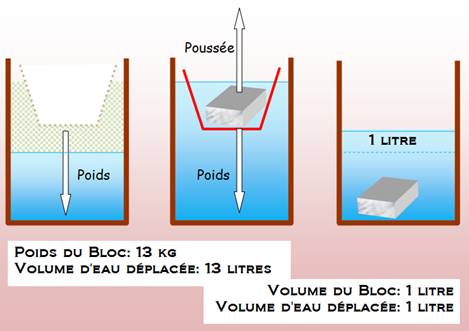
Énigme Un bateau flotte sur l'eau avec son équipage, des
figures en plomb. Le bassin est rempli d'eau à ras bord. L'équipage tombe à l'eau. Est-ce que le bassin
déborde? Solution Non, même, en principe le niveau va baisser. Explication (exemple de l'illustration) Le bateau et les figurines déplacent un grand
volume d'eau (13 l) égal au poids des figurines. Les figurines dans l'eau ne font monter l'eau que
de leur volume (1l). |
On néglige l'effet du bateau qui sert seulement à faire flotter le bloc de métal. |
|
|
|
||
|
Données Une
piscine rectangulaire de 10 x 5 m².
Le
couple sort de la piscine en emportant un film de 1 mm d'épaisseur sur leur
surface dans l'eau. De
combien baisse le niveau de la piscine? |
Commentaires On suppose que chacun fait la
planche de sorte que tout le corps est pratiquement immergé. Les deux corps
recouvrent ainsi une section de 0,8 + 0,7 = 1,5 m² (vu du ciel) sur les 50 m²
de la piscine. Cette surface sera nécessaire pour calculer la poussée
d'Archimède. Le film d'eau recouvre la surface
complète des deux corps soit: 2 + 1,5 = 3,5 m². Cette surface n'est
nécessaire que pour tenir compte du film d'eau sorti de la piscine lorsque le
couple en sort. |
|
|
Calculs Les deux corps sont immergés. Ils déplacent une
quantité d'eau V correspondant à leur poids P. |
P = 75 + 65 = 140 kg V = 140 litres = 0,14 m3 |
|
|
Ce déplacement d'eau s'exerce sur la surface disponible
de la piscine |
Sd = 50 – 1,5 = 48,5 m² |
|
|
Hauteur
correspondante |
|
|
|
Volume d'eau sur les corps (film de 1 mm sur toute la
surface de la peau) |
v = 3,5 x 10-3 m3 |
|
|
Hauteur
correspondante (sur toute la
surface de la piscine) |
|
|
|
Baisse du niveau de la piscine: d'abord l'eau qui
reprend sa place dans le trou laissé par les corps et, en plus, l'eau sortie de la piscine par les
corps mouillés. |
B = 2, 88 + 0,07 = 2,95 mm Soit, de l'ordre de 3 mm |
|
Voir Unités
/ Calcul sur les puissances
|
Eurêka! N =
Tout
nombre entier est la somme de trois nombres triangulaires. Voir Généralisation avec le théorème de Waring |
|
|
Archimedes Principle: Any object completely or partially
immersed in a liquid, is buoyed up with a force which is equal to the weight
of the fluid that the object displaces. or, Archimedes' principle states that
the upward buoyant force that is exerted
on a body immersed in a fluid, whether fully or
partially submerged, is equal to the weight
of the fluid that the body displaces and acts in the upward direction
at the center of mass of the displaced fluid. |
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Aussi |
|
|
Site |
|
|
Cette page |