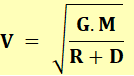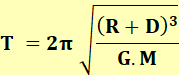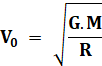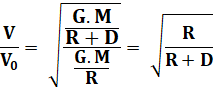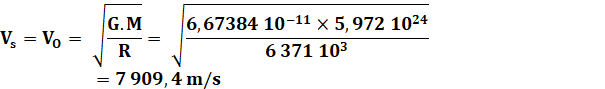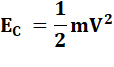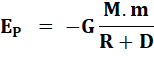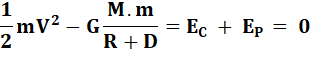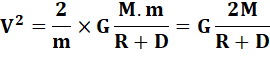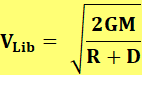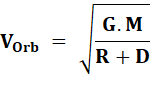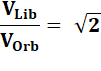|
||||||||||||||||||||||||||||||||||||||||
![]()
|
VITESSES COSMIQUES Quelle
est la vitesse orbitale à communiquer à un
corps (satellite, sonde …) pour qu'il se maintienne sur son orbite?
Note: cette page d'initiation reste très théorique. On néglige les
paramètres qui rendent délicats les calculs comme par exemple: l'effet de la
gravitation du Soleil, la friction sur l'atmosphère, le renflement de la
Terre et sa densité non-homogène … |
|
|
||
|
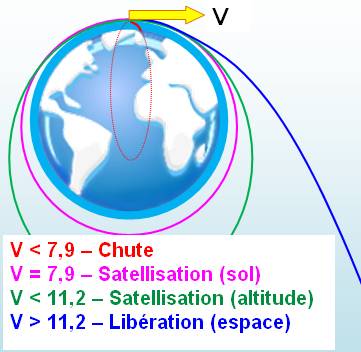
Au sol Imaginons
un super canon qui lance un engin avec une très grande vitesse. Normalement l'engin retombe sur la Terre après
avoir parcouru une trajectoire parabolique (petit morceau de courbe en rouge). Et si, on lançait l'obus très fort, tellement
fort qu'il dépasse la Terre. Oui, c'est possible! Il y a même deux possibilités:
Sur l'illustration, on montre les vitesses nécessaires (en km/s) pour
arriver à ces résultats. Des vitesses importantes: 7,9 km/s, c'est presque 40
000 km/h; quarante fois la vitesse d'un avion de ligne. |
Les
trajectoires possibles
D'après une idée vue en
Lumières
sur l'Univers –
Observatoire de Paris |
|
|
En
altitude On
retrouve les mêmes effets en altitude:
Mais, le
gros problème, c'est de mettre en place le "super canon" là-haut ! |
Satellites
(orbite autour de la terre) Deux moyens pour
atteindre l'altitude requise
Sondes
spatiales (exploration de l'espace) Un autre effet magique
est utilisé: l'effet catapulte due à de l'effet de gravitation au passage à
proximité d'une planète. |
|
En bref pour un objet autour de la Terre
|
Vitesse |
Corps (Lanceur, satellite, sonde …) |
|
< VC1 |
Le satellite retombe sur la Terre, comme ce serait le cas d'un obus
lancé d'un canon. |
|
VC1=
7,9 km/s 28 440 km/h |
Première vitesse cosmique Vitesse minimale de satellisation
d'un satellite au ras de la Terre. Le satellite est placé en orbite
circulaire à distance D de la Terre. |
|
de VC1
à VC2 |
Le satellite a une trajectoire circulaire ou elliptique de taille de
plus en plus importante avec la vitesse. |
|
VO |
Vitesse orbitale (fonction de l'altitude) Vitesse à maintenir pour rester sur une certaine orbite à une altitude
donnée. Par exemple pour une orbite géostationnaire (altitude 35 786 km), la
vitesse orbitale est 3,1 km/s. |
|
VC2
= 11,2 km/s 40 320 km/h |
Deuxième vitesse cosmique Vitesse de libération d'un
satellite quittant la Terre. |
|
> VC2 |
Le satellite échappe définitivement à l'attraction gravitationnelle de
la Terre en suivant une parabole
ou, plus vite, une hyperbole. |
|
VC3
= 42,1 km/s 151 560 km/h |
Troisième vitesse cosmique Vitesse de libération d'un satellite quittant le système solaire
(référentiel héliocentrique). |
![]()
|
|
||
|
Un satellite en orbite autour de la Terre est soumis à l'attraction
terrestre et devrait tomber. C'est sa vitesse qui crée une force centrifuge
telle qu'il est maintenu sur son orbite. L'intensité de cette force doit être
telle qu'elle compense la force d'attraction. Alors le satellite est en
équilibre et poursuit sa route sur sa trajectoire. Comment calculer la vitesse à communiquer à un satellite pour le
maintenir sur une orbite à une altitude donnée? |
||
|
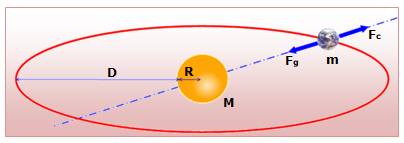
Formulation La
Terre tourne autour du Soleil. On
suppose que l'orbite est circulaire. Deux
forces en présence:
Elles
s'équilibrent:
Longueur
de l'orbite à l'altitude D: L = 2 Période: T = L / V |
Vitesse orbitale
Notez
que la vitesse orbitale ne dépend pas de la masse du satellite. Période orbitale
|
|
Application numérique
à un satellite autour de la Terre
|
Avec G = 6,67 10-11 constante
de la gravitation universelle. M = 5,98 1024 kg masse
de la Terre R = 6 378 km rayon de la Terre D altitude ou |
Vitesse orbitale à l'altitude 0
Vitesse orbitale en fonction de V0
|
|
|
Valeur de la vitesse orbitale au sol (D = 0)
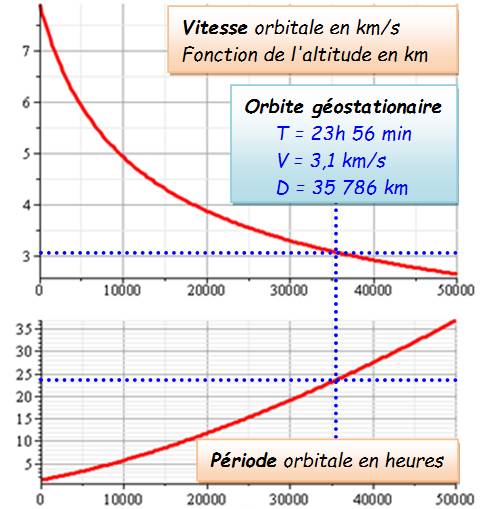
Courbes vitesse orbitale et durée orbitale
en fonction de l'altitude |
||
|
La
vitesse nécessaire pour maintenir le satellite en orbite (en équilibre)
décroit avec l'altitude; normal, les effets de la pesanteur diminuent. Pour
une distance nulle (au sol), on retrouve bien 7,9 km/s pour la vitesse
orbitale. Avec
une vitesse de 3,1 km/s, le satellite est maintenu à une altitude de 35 786
km et la période de révolution sur
l'orbite est égale à un jour (23h 56
min). Le satellite suit exactement la rotation de la Terre. Il est en
permanence à la verticale du même point. L'orbite est géostationnaire. Pour la Lune à environ 360 000
km, la vitesse orbitale varie de 0,97 à 1,08 km/s pour une révolution en
27,322 jours. |
|
|
Merci à Gilles Munsch
|
|
||||
|
Première vitesse cosmique Vitesse minimale de satellisation
d'un corps autour de la Terre. Vitesse minimale qu'il faut communiquer à
un corps à partir du sol pour qu'il ne
tombe plus sur Terre mais se mette en orbite. C'est en fait, la vitesse orbitale au sol (D = 0). |
VC1 = VS
= V0 = 7,9 km/s =
28 440 km/h |
|||
|
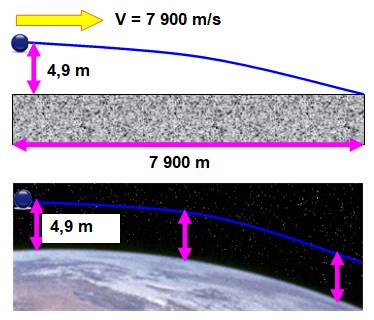
Ce qui se passe … la chute sans toucher le sol En haut, une bille est lancée depuis une
hauteur de 4,9 m, temps qui lui faut pour atteindre le sol en 1 seconde.
Durée identique, quelle que soit sa vitesse horizontale. Justement, avec une
vitesse horizontale de 7,9 km/s, la bille touchera le sol 7,9 km plus loin. Oui, mais, si nous sommes sur la Terre!
Elle est ronde et sa courbure est justement de 4,9 m tous les 7,9 km. La
bille ne peut plus toucher le sol qui, sur la distance, s'est escamoté de la
même hauteur. À tout instant la bille tombe, mais la Terre
s'échappe d'autant. Finalement, la bille est en rotation autour de la Terre;
elle est satellisée. |
Sur une idée vue en Principes
de satellisation – Cnes |
|||
|
Astronautes dans la station spatiale
internationale |
Si les astronautes se retrouvent en apesanteur
(ils ne ressentent plus leur poids) ce n’est pas parce qu’il n’y a plus de
gravité dans l’espace, ni parce que la gravité exercée par la Terre y est
trop faible (elle est presque identique à celle sur Terre). En réalité, les astronautes
chutent à la même vitesse que le satellite
vers la Terre. Ils se retrouvent dans la même situation qu’une personne se
trouvant dans un ascenseur en
chute libre, ils sont toujours soumis a la gravitation mais par rapport à
l’ascenseur et à tous les objets qui s’y trouvent, ils ont l’impression de
flotter. |
|||
|
|
|
||
|
Pas
facile d'arriver sur l'orbite désirée! Il
faut d'abord se hisser au-dessus de l'atmosphère. Une fois sur place, c'est
plus facile d'aller plus haut. Mise en orbite en trois phases:
Exemple: deux
minutes après le décollage, Ariane 5 atteint la vitesse de 2 km/s. |
Le lanceur (la fusée) décolle du pas de tir
en emportant sa charge utile (satellites ou sondes) logée dans sa tête. En interprétant la formule
de la vitesse orbitale, il ne faudrait pas conclure qu'il est plus facile
de placer un satellite sur une orbite éloignée que sur une orbite proche,
puisqu'il lui faut moins de vitesse. Dans le calcul de la vitesse d'ascension
(phase de translation) intervient un
terme qui représente la diminution de vitesse subie par le lanceur
dans son ascension verticale. Ce terme devient vite très grand et très
pénalisant. On gagne un peu de vitesse au lancement en
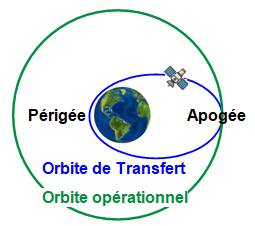
dirigeant le satellite La solution la plus économique pour placer
un satellite sur une orbite éloignée de la Terre est le transfert (Illustration).
C'est-à-dire, une fois sur orbite (vers 200 km) et à son apogée, lui communiquer
une faible vitesse complémentaire qui le fera passer sur une orbite beaucoup
plus lointaine (36 000 km, par exemple). Note: Les
satellites sont placés en orbite au-dessus de 200 km d'altitude pour éviter
qu'il ne soit freiné par l'air, et
retombe fatalement dans l'atmosphère tout en se consumant. D'ailleurs,
une coiffe thermique habille le nez du lanceur jusqu'à ces altitudes. Elle
est larguée ensuite. |
||
|
|
|||||
|
Deuxième vitesse cosmique Vitesse de libération d'un objet
quittant la Terre. À cette vitesse et au-delà, le corps échappe définitivement à l'attraction
gravitationnelle de l'astre en suivant une parabole puis, pour de plus
grandes vitesses, une hyperbole. C’est la vitesse qu’un objet doit atteindre afin de s’affranchir de
l’attraction gravitationnelle de la Terre d’où il est parti. Sortir du champ gravitationnel d’une plus grosse planète nécessite une
plus grande vitesse de libération. |
VC1 sur Terre = 11,186 km/s = 44 270 km/h Photo:
Ariane 5 au
décollage |
|
|||
|
Avec une vitesse supérieure à la vitesse de libération, le corps
s'éloigne; il pourra être soumis à la gravité d'autres astres. Le
lanceur utilise son énergie pour accélérer et atteindre progressivement la
vitesse de libération. Pourrait-on
obtenir le même résultat en utilisant une sorte de canon qui impulse cette
vitesse d'un coup à la Jules
Verne dans le roman De la Terre à
la Lune ? |
Effet
Le
phénomène de libération est responsable du fait que certaines planètes ont
perdu leur atmosphère. Il est aussi à l'origine de la formation des trous noirs. |
||||
|
Formulation Il
faut faire intervenir le principe de conservation d'énergie en considérant
que le système Terre-lanceur est un système fermé. |
Énergie potentielle
+ Énergie
cinétique = K |
||||
|
Énergie
cinétique |
|
||||
|
Elle
est négative, tendant à ramener l'objet vers la Terre. Elle est nulle à
l'infini. |
|
||||
|
Condition
de la libération Le
lanceur atteint la vitesse minimale qui lui permet d'échapper à la
gravitation de la Terre. |
EC = 0 Le
lanceur poursuit son chemin à l'infini. EP = 0 Le
lanceur n'est plus attiré par la Terre |
||||
|
Conservation
de l'énergie |
|
||||
|
Calcul
de la vitesse de libération |
|
||||
|
À
rapprocher de la vitesse orbitale Les
deux sont dans le rapport 1,414… Pour
la Terre: 7,9 x 1, 414 = 11, 2 km/s. |
|
||||
|
En pratique |
Pour
pouvoir échapper à l’attraction de la Terre, une sonde doit bénéficier d’une
impulsion suffisante: la vitesse de libération
est la vitesse minimale théorique que doit atteindre un corps à une altitude
donnée pour s’éloigner définitivement de la Terre. A
partir de la surface, s’il n‘y avait pas d’atmosphère, un boulet de canon
devrait ainsi être projeté verticalement à la vitesse de 11,2 km/s pour ne
plus jamais retomber. En pratique, la vitesse de libération, communiquée à la
sonde par le lanceur, est calculée en fonction de l’altitude au point
d’injection. À 36 000 km d’altitude, elle ne vaut ainsi plus que 4,3 km/s. Extrait
de Quitter la
Terre – Cnes |
||||
|
|
||||
|
Astre |
km/h |
km/s |
Commentaires |
|
|
Lune |
8 568 |
2,38 |
Vitesse maximum d'un avion: plus de 3 530 km/h (Mach + de 3,2) – Lockheed
SR-71 Blackbird (Merle) |
|
|
Terre |
40 270 |
11,186 |
Vitesse qui permettrait de faire le
tour de la Terre (Équateur) en une heure. Vitesse record d'un engin spatial:
50 000 km/h – Sonde New Horizons
(exploration de Pluton) |
|
|
Mars |
18 000 |
5 |
||
|
Jupiter |
2 424 230 |
60,20 |
|
|
|
Soleil |
2,223 106 |
617,5 |
Soit: 57 fois celle de la Terre,
mais 0,2 % la vitesse de la lumière.
La lumière n'a pas de peine à s'échapper du Soleil. |
|
|
500 Soleils |
108 |
300 000 |
Astre d'un diamètre 500 fois
supérieur au Soleil, Soit, la taille de l'orbite de Jupiter. |
|
Voir Calcul de la
vitesse de libération
|
|
||
|
Trou noir: un astre,
suffisamment grand ou dense pour que sa vitesse de libération dépasse celle de la lumière, retiendrait les
particules de lumière! Cette conclusion a été imaginé
séparément par : |
||
|
Michell (anglais)
- 1783 |
Pierre Laplace
(français)
- 1796 |
|
|
500
fois le diamètre du Soleil Non-luminiferous
bodies "Mais
ce sont des considérations qui dépassent mon propos, et je m'arrête là." |
250
fois le diamètre du Soleil avec la densité de la Terre. Les
corps obscurs. Il
retire cette notion de sa dernière publication (1808). A cette époque on dit
que la lumière ne serait pas faite de particules, mais se comporterait comme
une onde! (Young et Fresnel). |
|
|
On comprend mieux le gigantisme des
lanceurs utilisés pour atteindre ces vitesses cosmiques. Une fusée comprend
en général trois étages: le premier amène le tout à une vitesse V1.
Le deuxième lui communique une vitesse V2 supplémentaire et le
dernier lui ajoute encore V3. Soit la somme des trois vitesses. Le premier satellite artificiel fut Spoutnik,
lancé en 1957 par l'URSS. Il pesait 83,6 kg. En 1965, la France lance son
premier engin: Astérix. |
Merci à
Olivier C. pour ses conseils précieux
![]()
|
Suite |
|
|
Voir |
|
|
Aussi |
|
|
Diconombre |
|
Sites |
|
|
Cette page |