|
|||||||||||||||||||||||||||||||||||
![]()
|
Problèmes basiques liés au temps de travail Quelques exemples et une
approche illustrée pour visualiser et résoudre ce type de problème. |
|
|
||
|
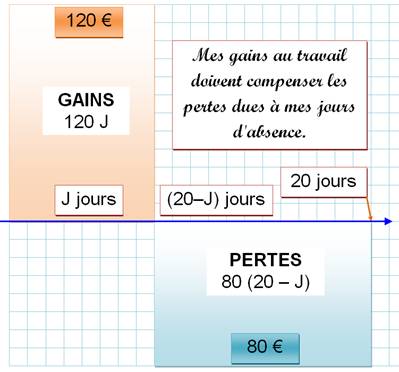
Problème
|
||
|
Approche du problème
|
|
|
|
Solution
|
gains
= 120 J pertes
= 80 (20 – J) 120
J = 1600 – 80 J |
|
|
Calcul pas à pas Notes: 120J veut dire 120
multiplié par J; J est une lettre qui remplace la quantité de jours cherchée,
valeur inconnue au départ. En algèbre, l'inconnue est généralement notée
"x". Ici, nous évitons pour ne pas confondre avec le signe
multiplier (x). |
120J
+ 80J = 1600 – 80J + 80J 200J
= 1600 200J
/ 200 = 1600 / 200 J
= 8 Voir
Initiation au calcul algébrique |
|
|
Vérification |
8 x 120 = 720 € de gains. 12
x 80 = 720 € de pertes. |
|
|
|
|||
|
Problème
|
|||
|
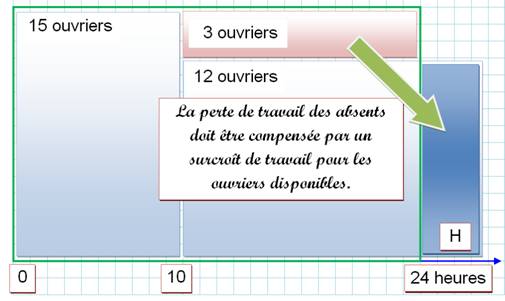
Approche du problème La quantité de travail non réalisée par les ouvriers
absents doit être compensée par une quantité de travail équivalente par ceux
qui sont présents. Les deux surfaces montrées par la flèche verte sont
égales. |
|
||
|
Solution
|
3 x (24 – 10) = 3 x 14 = 42 12 x H 12 x H = 42 |
||
|
Calcul pas à pas |
12 x H / 12 = 42 / 12 H = 14 / 4 = 7/2 = 3,5 heures |
||
|
Bilan |
Les ouvriers présents devront travailler 3,5 heures de
plus. Soit 24 + 3,5 = 27,5 heures. |
||
|
Vérification |
Quantité de travail à fournir: 15 x 24 = 360 heures Quantité de travail réalisée: 15 x 10 + 12 x (14 + 3,5) = 150 + 210 = 360 heures. |
||
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()