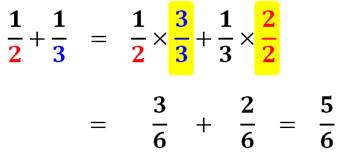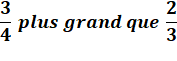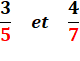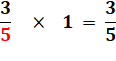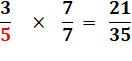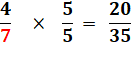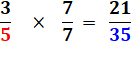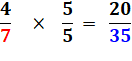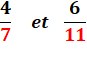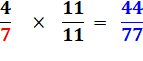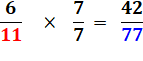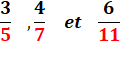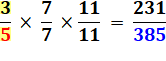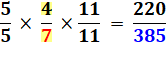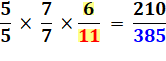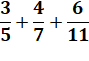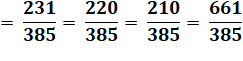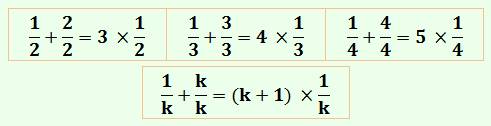NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 01/04/2020 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
Débutants Général	Type de nombres
Junior Découverte des fractions	FRACTIONS				Glossaire Fraction
INDEX Fractions Calcul	Débutant	Dénominateur	Multiplication	Règle de trois
	Construction	Comparaison	Unitaire	Calculs (exemples)
		Sommaire de cette page >>> En bref >>> Approche illustrée >>> Même dénominateur – Deux fractions >>> Deux autres >>> À trois >>> Énigme pour pratiquer le calcul des fractions

FRACTIONS

Réduction au même dénominateur

Débutants

Comment découper les tartes pour comparer les parts données à chacun ou pour ajouter les parts? Explications pas à pas.

Eh oui! On ajoute des tiers avec des tiers mais pas des tiers avec des quarts. Alors on divise plus fin pour avoir des parts de même taille.

En bref

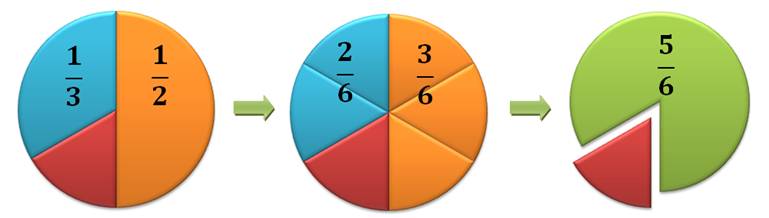
Illustration

Pour ajouter un demi à un tiers, je découpe la tarte en sixièmes.

La somme est visible immédiatement: cinq sixièmes.

Procédé

1) Multipliez avec la fraction unité formée avec le dénominateur de l'autre fraction. Avec 2 la fraction unité est 2/2. 2) Ayant le même dénominateur, ajoutez les numérateurs.

Voir Comment s'initier aux fractions avec le cadran d'une horloge

Approche illustrée
Comment comparer les deux morceaux choisis Un rectangle est découpé de deux manières différentes. celui du haut est découpé en 3 bandes et j'en prends 2, c'est la fraction 2/3; et celui du bas est découpé en 4 bandes et j'en prends 3, c'est la fraction 3/4. Question: quel est le morceau coloré le plus grand? Difficile de le savoir car la taille des bandes n'est pas la même. Compter la même chose dans tous les cas L'astuce évidente consiste à compter les petits carrés en haut nous en trouvons 8, et en bas il n'y en a que 9. C'est le morceau du haut qui est le plus grand: Lorsque vous avez compté les petits carrés, de même taille dans un cas comme dans l'autre, vous avez fait ce qui est appelé une réduction au même dénominateur.	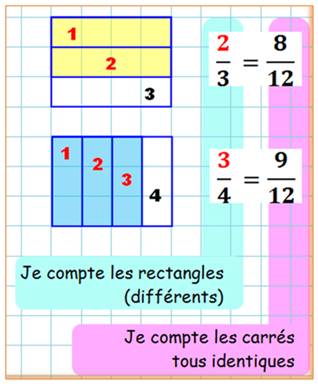Division du même rectangle de deux manières En comptant les petits carrés identiques, je compte la même chose en haut et en bas. Les fractions se retrouvent avec le même dénominateur.

Même dénominateur
Réduire au même dénominateur les deux fractions suivantes:
Nous sommes en face de deux tartes l'une découpée en 5 et l'autre en 7. En effet, le dénominateur indique en combien de parts est divisé la tarte. Les numérateurs (3 et 4) indiquent combine de parts nous prenons dans chaque tarte. Nathan en prend 3/5 et Lili en prend 4/7. Qui en a le plus? Est-ce que c'est bien équitable? Le seul moyen de le savoir est de réaliser des parts égales en découpant plus finement la tarte. La seconde est découpée en 7. Nous allons découper toutes les parts de la première en 7.
La seconde est découpée en 7. Alors, nous allons découper toutes les parts de la première en 7. Cela fait des toutes petites parts, mais j'en ai beaucoup plus. Sept fois plus bien évidemment! Les 3 parts deviennent 35 petits morceaux.	Multiplication de la fraction par 1: Remplaçons 1 par la fraction 7/7 qui vaut bien 1
Nous faisons la même chose avec la deuxième tarte. Nous partageons en 5 comme l'est la première tarte.
Nous avons maintenant deux tartes, chacune divisées en 35 parts. Nathan en a 21 morceaux alors que Lili en a 20, une de moins. Mais elle ne va pas se laisser faire …	En résumé, les deux fractions avec le même dénominateur.

Même dénominateur (suite 1)
Réduire au même dénominateur les deux fractions suivantes:
La seconde est découpée en 11. Alors, nous allons découper toutes les parts de la première en 11.
Nous faisons la même chose avec la deuxième tarte.

Même dénominateur (suite 2)
Réduire au même dénominateur les deux fractions suivantes:
Nous ne pouvons pas faire autrement que découper la première en 7 comme la deuxième puis en 11 comme la troisième. Même principe pour les deux autres. Notez l'arrangement des nombres.
La recherche du même dénominateur permet de comparer les fractions. C'est également la seule possibilité de les ajouter ou de les soustraire.

Devinette

Quelles sont les fractions x/y telles que si on leur ajoute la fraction y/y = 1, la fraction initiale est multipliée par k?

Exemples et solution:

Simplifier! – Mise en évidence d'une jolie cascade.

Mettre au même dénominateur:

Effectuer les soustractions

Simplifiez en imaginant toute la suite des termes:

le dénominateur de l'un se simplifie avec le numérateur du suivant.

Niveau primaire avancé ou collège

Énigme pour pratiquer le calcul des fractions
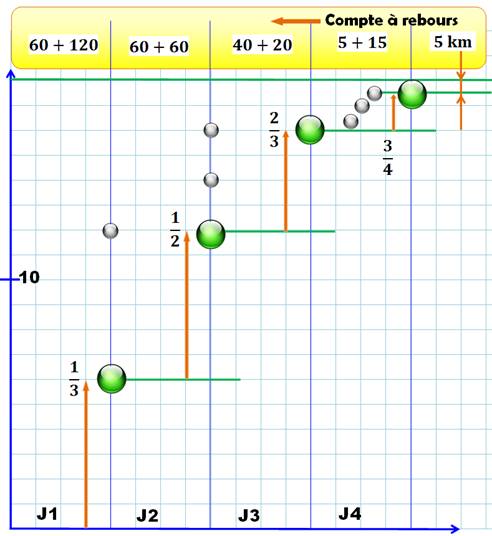
Énigme En quatre jours, un coursier à cheval constate son parcours quotidien (ci-contre =>). Quelle est la distance parcourue?	Jour 1: il fait le tiers du parcours; Jour 2: il fait la moitié du reste; Jour 3: il fait les 2/3 du reste; et Jour 4: il fait les 3/4 du reste, vérifie son courrier et fait les derniers 5 km qui le séparent de sa destination.
Deux méthodes sont présentées: La solution graphique qui fait un compte à rebours à partir des 5 km finaux; et La solution par calcul des fractions.

Solution graphique En bas, on note les quatre jours, J1, J2, J3 et J4. En vertical, on montre la distance parcourue. Un carreau = 10 km. En haut, on place une barre horizontale verte qui symbole la longueur du trajet (L) Au jour 4, on place une marque (bille verte) à 5 km en-dessous du but. Les petites billes grises montrent les fractions. Commençons le compte à rebours (encadré jaune). Lorsque le coursier vérifie son courrier, il a fait 3/4 du reste à faire. Il ne reste plus que 1/4 à faire, lequel vaut 5 km. C'est que le reste à faire est égal à 4 x 5 = 20 km. Celui-ci représente le tiers du reste à faire du jour 3, lequel est donc égal à 3 x 20 = 60 km. Celui-ci représente la moitié du reste à faire du jour 2, lequel est donc égal à 2 x 60 = 120 km. Finalement, cette distance représente les 2/3 du trajet total, lequel vaut alors: 120 x 3/2 = 180 km

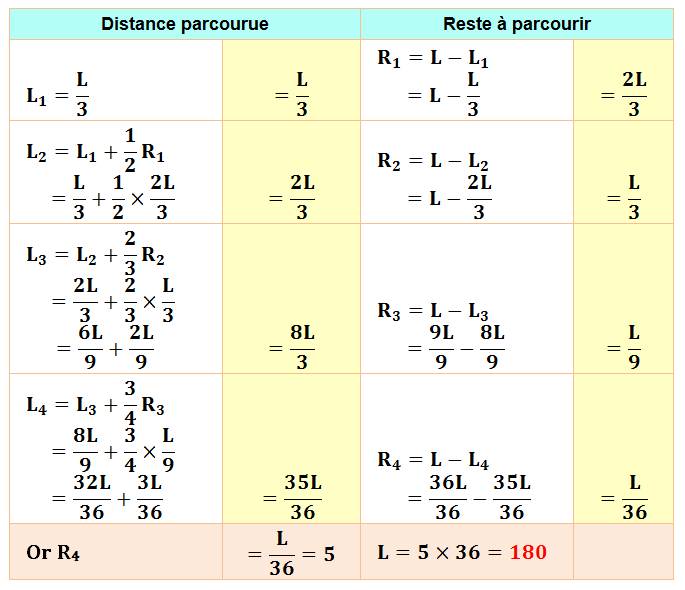
Illustration Solution: longueur du trajet: 180 km Jour 1: il fait le tiers du parcours: 180 / 3 = 60 Jour 2: il fait la moitié du reste: (180 – 60) /2 = 60 Jour 3: il fait les 2/3 du reste: 60 x 2/3 = 40 Jour 4: il fait les ¾ du reste, vérifie son courrier et fait les 5 km qui le sépare de sa destination: 15 + 5 km.

Solution algébrique: calcul des fractions

Voir Énigmes

Retour	Fractions débutants – Autres exemples
Suite	Multiplication de fractions Fractions à étages Fractions illicites Fractions amusantes Fractions – Glossaire et index Fractions – Découverte Junior
Voir	Autres fractions avec les chiffres du nombre Fractions égyptiennes – Tables Règle de trois
Aussi	Calculs – Initiation Calculs avec les horloges Horloge Jeux, énigmes … Motifs Nombres magiques Pépites Suite harmonique
Cette page	http://villemin.gerard.free.fr/Calcul/Fraction/Denomi.htm