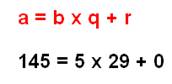|
||||||||||||||||||||||||||||||||||||||||
![]()
|
PREUVE PAR 9 En anglais: chasser les neufs
-
Qui est en fait la somme des
chiffres du nombre. -
La valeur 9 étant assimilée
à 0. -
Nous expliquerons pourquoi ci-dessous.
-
La racine théosophique ou racine essentielle. -
La valeur 9 est conservée. -
Car toutes les valeurs des chiffres sont
significatives:
|
Anglais: Cast out the nines, digital root
|
|
|
|
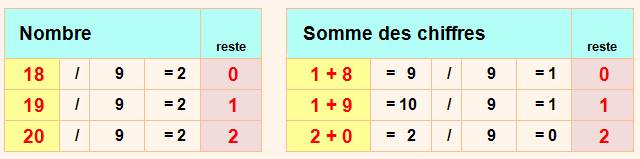
Observations
Si on divise le nombre ou la somme de ses chiffres par 9, on obtient le même reste. Voir
Preuve par neuf: théorie et
magie La magie de la preuve par neuf tient à
cette observation. Notez
bien que: la somme
des chiffres est aussi un nombre et la
somme de ses chiffres divisée par 9 redonnera à nouveau le même reste Et on peut
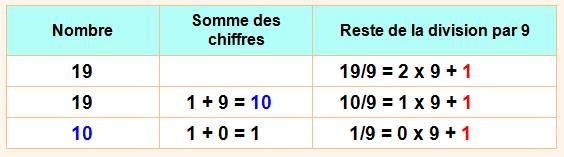
continuer … Il faut
donc procéder à la somme des chiffres jusqu'à l'obtention d'un nombre à un
seul chiffre.
|
|
|
|
||
|
Règle 1) On ajoute les chiffres du nombre. 2) On élimine tous les 9 qui apparaissent. La
quantité d'opérations à réaliser est parfois appelée le rang de la racine numérique. Pour bien
comprendre Racine numérique de:
|
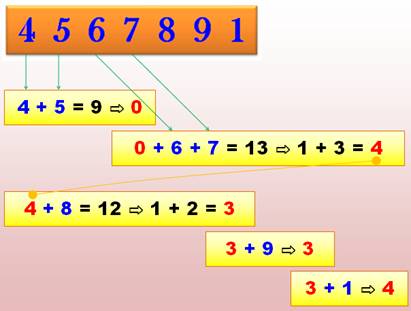
Exemple:
Calculer la racine numérique de ce nombre
4 + 5 = 9 et 9 est équivalent à
0. 6 + 7 = 13; en reprenant les chiffres de 13: 1 + 3 = 4; ce résultat (4) est ajouté au chiffre suivant (8); etc. Conclusion: La racine numérique de 4567891 est 4. Ce qui veut dire que: le reste de la division par 9 de ce nombre est
4. |
|
|
|
||
|
La
racine numérique d'un nombre est simple à calculer et c'est une vraie chance
pour vérifier une opération arithmétique car: Une opération juste est également juste en utilisant les racines
numériques Attention: ce n'est pas vrai dans l'autre sens. |
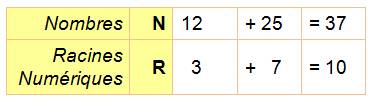
Exemple
La "vraie" opération 12 + 25 = 37 et sa racine numérique est
3 + 7 = 10 soit 1; L'opération avec les racines numériques des opérandes donne 3 + 7 = 10
soit 1, le même résultat. |
|
|
|
||
|
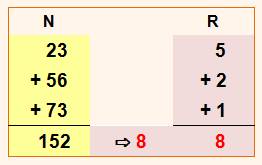
En pratique À côté de l'addition, on réserve une
colonne dans laquelle on écrit les racines numériques. On vérifie que la somme dans la colonne des
R est égale à la racine numérique du résultat. |
|
|
|
|
||
|
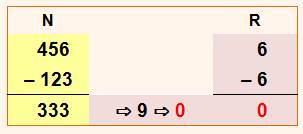
En pratique Colonne créée pour les R. On vérifie que la différence des R est
égale à la racine numérique du résultat. |
|
|
|
Astuce Pour vérifier l'égalité, souvenez vous que
les 9 disparaissent, mais vous pouvez en ajouter, notamment pour éviter les
nombres négatifs. |
Exemple 4045
– 2095 = 1050
En
ajoutant 9, l'égalité est bien là: –3 + 9 = 6. |
|
|
|
||
|
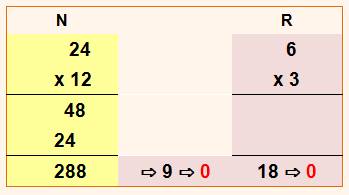
En pratique On dessine une croix En haut et en bas, on place les racines
numériques des deux opérandes (6 et 3) La racine numérique (0) de leur produit
(6x3) est inscrite à droite. On vérifie à gauche que la racine numérique
(0) du produit "vrai" (288) est bien égale à celle trouvée à
droite. Avec l'habitude, le calcul des racines
numériques se fait de tête et les résultats sont inscrits directement dans la
croix. |
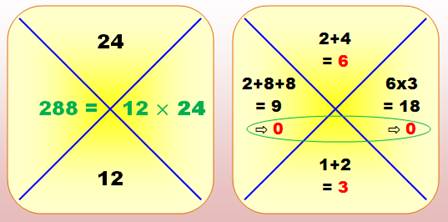
Présentation
pour la compréhension
Opération
complète et son image en racines numériques
Présentation
en pratique
|
|
|
|
|||
|
Un tout petit
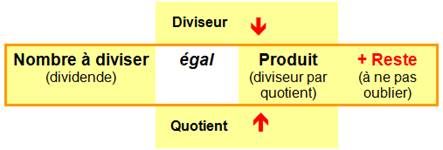
peu de théorie Pour la division,
la preuve par 9 est simple si on se souvient bien de ce qu'est une division. La preuve par 9
de la division est l'image de cette opération. |
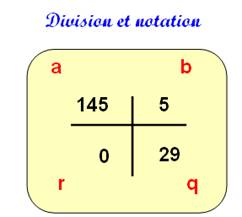
Quand on divise a par b on obtient un quotient q et un reste r: a = b . q + r Exemple 257 = 7 x 36 + 5 En preuve par 9, ça donne: 5 &
7 x 9 + 5 => 5 |
||
|
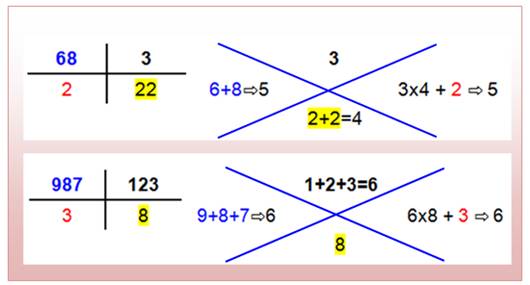
Mécanique de
la preuve par neuf de la division Comme pour la
multiplication, l'usage veut que l'on dessine une croix. La première
figure montre les notations La seconde, en
bas, montre la disposition des nombres et le calcul effectué:
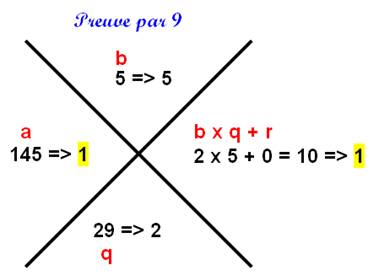
La vérification
consiste à comparer les deux chiffres à droite et à gauche. |
|
||
|
Disposition à
retenir |
|
||
|
Exemples |
|
||
|
|
||
|
Si la preuve par
9 échoue, |
|
|
|
Le
résultat de l'opération est faux. |
L'opération
n'est pas
forcément exacte. |
|
|
Si la preuve par
9 donne un bon résultat, il se peut que plusieurs erreurs se compensent. C'est pourquoi le
résultat de l'opération n'est pas forcément juste. Mais, avec cette
vérification, la probabilité que l'opération soit juste est tout de même très
grande. |
||
![]()
|
Suite |
|
|
Débutants |
|
|
Voir |
|
|
Cette page |
![]()