|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Racines numériques (ou
résidus) Additives et Multiplicatives Additions ou multiplications itératives
sur les chiffres d’un nombre. La persistance (r) indique la quantité
d’opérations à effectuer pour terminer l’itération (arriver à un seul
chiffre). Exemples
|
Anglais:
Additive
digital root / Multiplicative digital root /
Additive
persistence / Multiplicative persistence
Propriété fondamentale
|
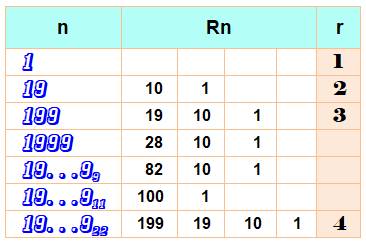
En termes de résultats: RN+(n) = n mod 9 La racine numérique additive est égale au nombre modulo 9
(le reste de la division par 9). Exemple: n = 123 =>
RN+ = 1 + 2 + 3 = 6 et 123 / 9 = 13 x
9 + 6
|
Voir Astuces tableur (somme des chiffres)
|
|
|||
|
|
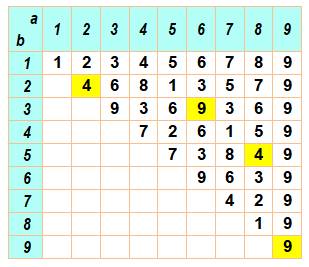
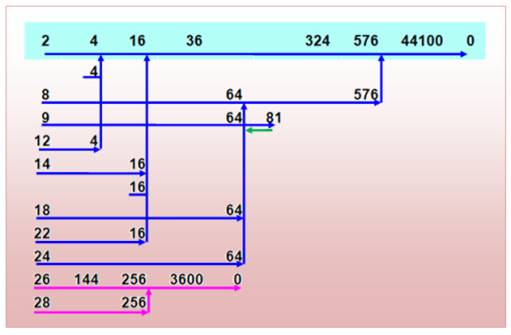
Nombre 11 222 567 888 888 |
Racine
Num. 2 r1 6 r1 18 9 r2 48 12 3 r3 |
|
|
|
1 999 999 181 270 362 |
1
r3 3 Sans raccourci 30 3
r2 |
|
|
|
||
|
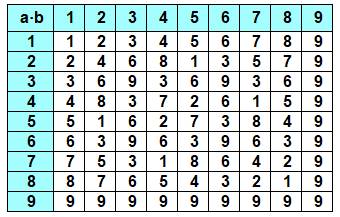
Quelle est la racine numérique du produit de deux nombres ? Exemple 12 x 34 = 408 RN: 3 x 7 = 21 => 3 RN: 408 => 12 => 3 En jaune le cas ou le produit correspond aussi à la somme. Exemple 8 x 473 = 3 784 RN: 8 x 5 => 4 RN: 3 784 => 4 et, en plus 8 + 5 + 13 => RN: 4 |
En jaune: produit = somme. Quatre cas avec comme résultat 4 ou 9
seulement. |
|
Voir Nombres
de Friedman multiplicatifs
|
Exemple:
N
= 789 789; Racine Numérique = 3; En trois calculs: r = 3 |
|
||||
|
80, 8, 1 81, 0, 1 82, 1, 2 83, 2, 2 84, 3, 2 85, 4, 2 86, 5, 2 87, 6, 2 88, 7, 2 89, 8, 2 90, 0, 1 91, 1, 2 92, 2, 2 93, 3, 2 94, 4, 2 95, 5, 2 96, 6, 2 97, 7, 2 98, 8, 2 99, 0, 2 |
150, 6, 1 151, 7, 1 152, 8, 1 153, 0, 1 154, 1, 2 155, 2, 2 156, 3, 2 157, 4, 2 158, 5, 2 159, 6, 2 160, 7, 1 161, 8, 1 162, 0, 1 163, 1, 2 164, 2, 2 165, 3, 2 166, 4, 2 167, 5, 2 168, 6, 2 169, 7, 2 170, 8, 1 |
980, 8, 2 981, 0, 2 982, 1, 3 983, 2, 2 984, 3, 2 985, 4, 2 986, 5, 2 987, 6, 2 988, 7, 2 989, 8, 2 990, 0, 2 991, 1, 3 992, 2, 2 993, 3, 2 994, 4, 2 995, 5, 2 996, 6, 2 997, 7, 2 998, 8, 2 999, 0, 2 |
789 789, 3, 3 789 790, 4, 2 789 791, 5, 2 789 792, 6, 2 789 793, 7, 2 789 794, 8, 2 789 795, 0, 2 789 796, 1, 3 789 797, 2, 3 789 798, 3, 3 789 799, 4, 3 789 800, 5, 2 789 801, 6, 2 789 802, 7, 2 789 803, 8, 2 789 804, 0, 2 789 805, 1, 3 789 806, 2, 3 789 807, 3, 3 789 808, 4, 2 789 809, 5, 2 789 810, 6, 2 789 811, 7, 2 789 812, 8, 2 789 813, 0, 2 789 814, 1, 3 789 815, 2, 3 789 816, 3, 3 789 817, 4, 2 789 818, 5, 2 789 819, 6, 2 789 820, 7, 2 |
999 980, 8, 2 999 981, 0, 2 999 982, 1, 3 999 983, 2, 3 999 984, 3, 3 999 985, 4, 3 999 986, 5, 2 999 987, 6, 2 999 988, 7, 2 999 989, 8, 2 999 990, 0, 2 999 991, 1, 3 999 992, 2, 3 999 993, 3, 3 999 994, 4, 3 999 995, 5, 2 999 996, 6, 2 999 997, 7, 2 999 998, 8, 2 999 999, 0, 2 |
|
|
Ce dernier nombre dépasse la
capacité de calcul de Maple, par exemple Voir OEIS A006050 – Smallest
number of additive persistence n |
|||||
Voir Racine
numérique avec des carrés et nombres heureux
|
|
||
|
Programme
simple avec Maple
|
Calcul de la racine numérique d'un
nombre Procédure de calcul de la racine numérique. La racine numérique R prend la valeur de n au départ. Tant qu'elle dépasse 9 on recommence le calcul. Celui-ci consiste à obtenir les chiffres
(convert) et à les additionner (add). |
|
|
Programme
récursif avec Maple
|
Calcul
de l'ensemble des racines numériques des carrés RN est une procédure, une fonction qui retourne
la racine numérique de n. Le nombre n est converti en sa suite de chiffres,
lesquels sont additionnés en s. Si cette somme s est à deux chiffres, elle est
réinjectée dans la procédure RN (principe du calcul récursif). La valeur finale de s est retournée vers le
programme d'appel. Le programme principal compose un ensemble –
présence des accolades { } – des diverses valeurs prises par la racine
numérique des carrés. Le point virgule final implique une impression. |
|
Voir Application aux nombres
polygonaux / Brève
808 / Programmation – Index
|
|
||
|
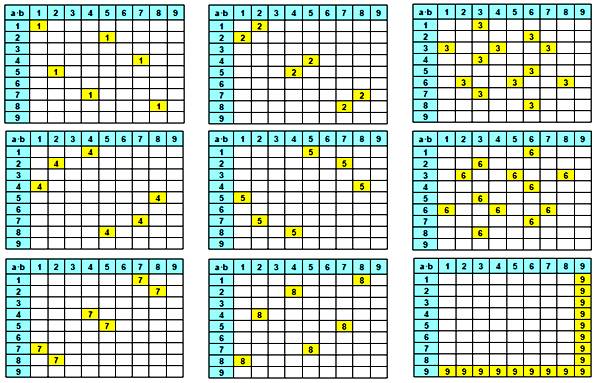
Racines de la table de 1 à 9
Chaque chiffre crée un motif régulier dans le tableau |
|
|
Répartition des racines numériques additives
Exemple de lecture: il y a 98
049 nombres composés avec RN = 1 jusqu'à 1 million;
il y a 0 nombre premier avec RN = 1 et en 6k – 1 ;
il y a 13 063 nombres premiers avec RN = 1 en 6k + 1; et,
il y a 111 112 nombres avec RN = 1 dans cette plage (y compris 1000 000).
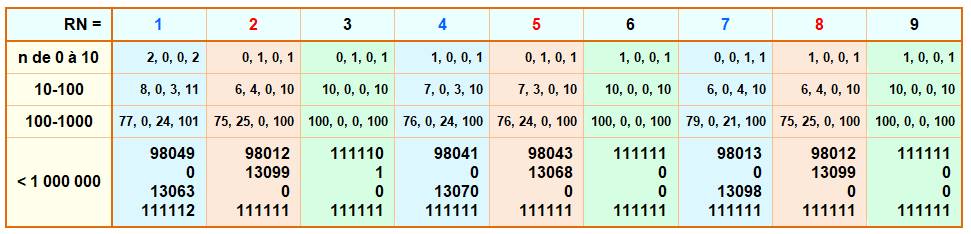
Une distribution assez homogène.
![]()
|
|
|||
|
|
12 123 99 |
2 6 8 |
|
|
|
|||||||||||||||||||||||||||||
|
La liste des
records de persistance multiplicative est sans doute finie :
|
|
||||||||||||||||||||||||||||
|
Suite par exemple: Généralisation à
la puissance k des chiffres. Record de
persistance des nombres premiers. |
Exemples de produits des CARRÉS des
chiffres
Le nombre 2
tient un record avec 7 itérations. |
||||||||||||||||||||||||||||
Voir Persistance
multiplicative – Records
|
|
||
|
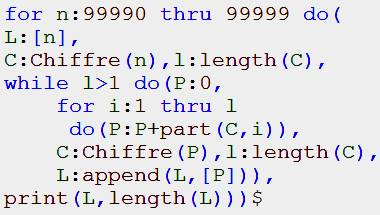
Programme Chiffre avec Maxima
Programme Persistance multiplicative
Sorties
|
Commentaires On charge la fonction Chiffre mis au point sur une autre page. Notre programme commence par une boucle d’analyse des nombres de 670 à
680 (par exemple). Initialisation d’un compteur (kt) et d’une liste (L). Appel à la fonction Chiffre qui liste les chiffres de n dans C.
Quantité de chiffre mis dans l. Tant que (while) cette longueur est
supérieure à 1, on poursuit les calculs itératifs sur les chiffres. Le produit des chiffres (P) est initialisé à 1. Boucle de calcul du produit des chiffres : le produit est calculé
avec le chiffre numéro i (part). Le produit est décomposé en ses chiffres mis dans C. Le produit est ajouté à la liste et le compteur est incrémenté. En fin de calcul sur n, impression de la liste des produits successifs
et de la quantité des itérations. Note : on aurait pu éviter la gestion du compteur et demander la
longueur de la liste finale. |
|
|
Persistance additive
|
Commentaires Le même programme adapté à la persistance additive. P est initialisé à 0 (et non 1). Et l’opération est l’addition et non la multiplication. On en profite pour supprimer le compteur au produit du calcul de la
longueur de la liste finale (L). |
|
Voir Programmation – Index
y compris liste des programmes Maxima
|
The digital sum D(n) of a positive integer is
defined recursively as follows:
where
For example: D(987) = D(24) = D(8) = 8 |
Voir Anglais pour le bac et
pour les affaires
![]()
|
Suite |
|
|
Voir |
|
|
Aussi |
|
|
Diconombre |
|
|
Sites |
|
|
Cette page |
![]()