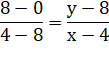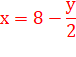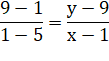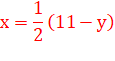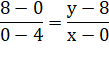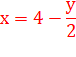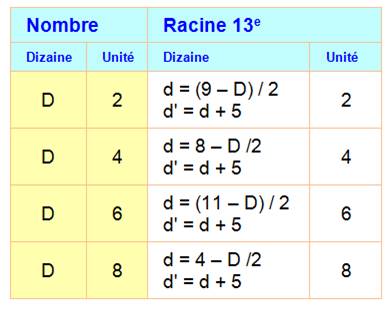
NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 04/07/2018 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique Brèves de Maths
	EXPOSANTS
Débutants Général	RACINES				Glossaire Général
INDEX Puissances et racines Analyse Calcul mental	Règles de base =>	Principe	Unités et dizaines	Poids forts
	2 chiffres =>	Dizaine impaire	Dizaine paire
		Sommaire de cette page >>> Nombres en …2 >>> Nombres en …4 >>> Nombres en …6 >>> Nombres en …8 >>> Nombres en …5

RACINE TREIZIÈME

Racine à deux chiffres

Dizaine paire

Exercice de calcul de racine treizième. Avec des unités impaires (sauf 5), le calcul est très simple, car la relation est biunivoque.

Avec des unités paires, la relation renvoie vers deux possibilités. Il faut lever l'ambiguïté.

Avec 5, avec 5 possibilités, cela devient très difficile.

Nombres en …2
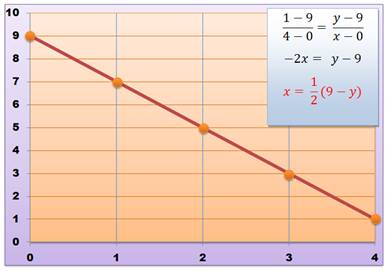
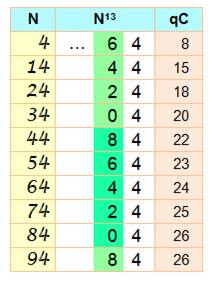
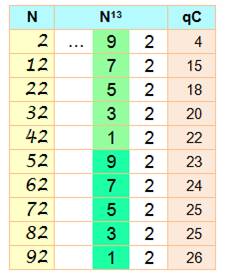
Mise en équation Le graphe des valeurs de la dizaine de N^13 en fonction de la dizaine de N et l'équation de la droite: Règle n°2-7 La dizaine de N est égale à la moitié de 9 moins la dizaine de N^13, à 5 près. La quantité de chiffres lève l'ambiguïté. Exemple 36 893 488 147 419 103 232 Sa racine 13^e : Unité: 2 Dizaine: 3 => (9 – 3)/2 = 3 ou 8 or 20 chiffres => 3 Soit: 32^13	qC: quantité de chiffres dans N^13.

Nombres en …4
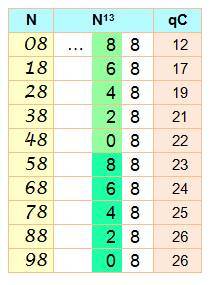
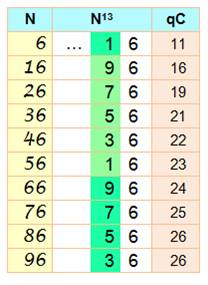
Mise en équation Règle n°2-4 La dizaine de N est égale à 8 diminué de la moitié de la dizaine de N^13, à 5 près. La quantité de chiffres lève l'ambiguïté. Exemple 302 231 454 903 657 293 676 544 Sa racine 13^e : Unité: 4 Dizaine: 4 => 8-4/2 = 6 ou 1 or 24 chiffres => 6 Soit: 64^13	qC: quantité de chiffres dans N^13.

Nombres en …6
Mise en équation Règle n°2-6 La dizaine de N est égale à la moitié de 11 moins la dizaine de N^13, à 5 près. La quantité de chiffres lève l'ambiguïté. Exemple 2 822 127 947 962 858 105 470 976 Sa racine 13^e : Unité: 6 Dizaine: 7 => (11-7)/2 = 2 ou 7 or 25 chiffres => 7 Soit: 76^13 (coquetterie: mêmes dizaines et unités, 76).	qC: quantité de chiffres dans N^13.

Nombres en …8
Mise en équation Règle n°2-8 La dizaine de N est égale à 4 diminué de la moitié de la dizaine de N^13, à 5 près. La quantité de chiffres lève l'ambiguïté. Exemple 18 979 061 712 307 928 304 713 728 Sa racine 13^e : Unité: 8 Dizaine: 2 => 4-2/2 = 3 ou 8 or 26 chiffres => 8 Soit: 88^13	qC: quantité de chiffres dans N^13.

Nombres en …5
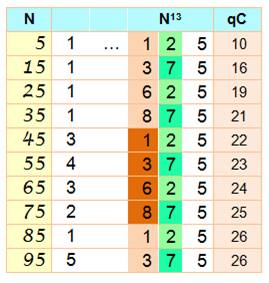
Observations Ce cas est plus le plus difficile. Il fait intervenir le premier chiffre et le chiffre des centaines. On procède par élimination en plusieurs étapes. Règle n°2-5 I) D et d ont même parité. II) Si qC = 26 => D = 8 ou 9. III) Si p = 1 et c<5 => D = 0 ou 1; c>5 => D = 2 ou 3. IV) Sinon, si c<5 => D = 4 ou 5; c>5 => D = 6 ou 7. Exemple 42 141 982 597 572 021 484 375 Sa racine 13^e : Unité: 5 Dizaine: 7 => D est impair Quantité de chiffres: 23 qui est < 26. Centaine: 3 qui est <5. Premier chiffre n'est pas 1 => D = 5 Soit: 55^13	Notons D le chiffre cherché et p…cdu les chiffres de la puissance 13. qC: quantité de chiffres dans N^13.

Bilan

La racine 13^e des nombres avec unité paire et ayant deux chiffres est connue de la manière suivante:

Unité = celle du nombre; et

Dizaine = d calculé comme indiqué sur le tableau. Un lever de doute entre d et d'est nécessaire en se référant à la quantité de chiffre de la puissance.

Pour les unités en 5, se référer au chapitre ci-dessus.

Suite	Voir haut de page Racine
Voir	Racine cinquième Puissance – Index
Site	Voir Liste
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Analyse/Racine13.htm